Eine Balkentafel ist eine Möglichkeit, wie man sich Brüche vorstellen kann. Eine Balkentafel zeigt, wie ein Ganzes auf mehrere Art und Weisen unterteilt werden kann. Jede Unterteilung ergibt jedoch wieder ein Ganzes. Eine Balkentafel kann zum Beispiel so aussehen:



1.) Anhand einer Balkentafel kann man beispielsweise einzeichnen, wieviel $\frac{2}{3}$ sind. Bei $\frac{2}{3}$ teilt man das Ganze in 3 Teile, also braucht man den 3er-Balken. Da man nun 2 dieser 3 Teile

möchte, markiert man 2 der 3 Balkenanteile.



2.) Anhand einer Balkentafel kann man auch zwei Brüche miteinander vergleichen. Will man

beispielsweise wissen, ob $\frac{1}{3}$ oder $\frac{1}{4}$ größer ist, so muss man sich den 3er-und den 4er-

Balken ansehen. Um die zwei Brüche miteinander zu vergleichen, markiert man dann die

zwei Anteile in der Balkentafel:



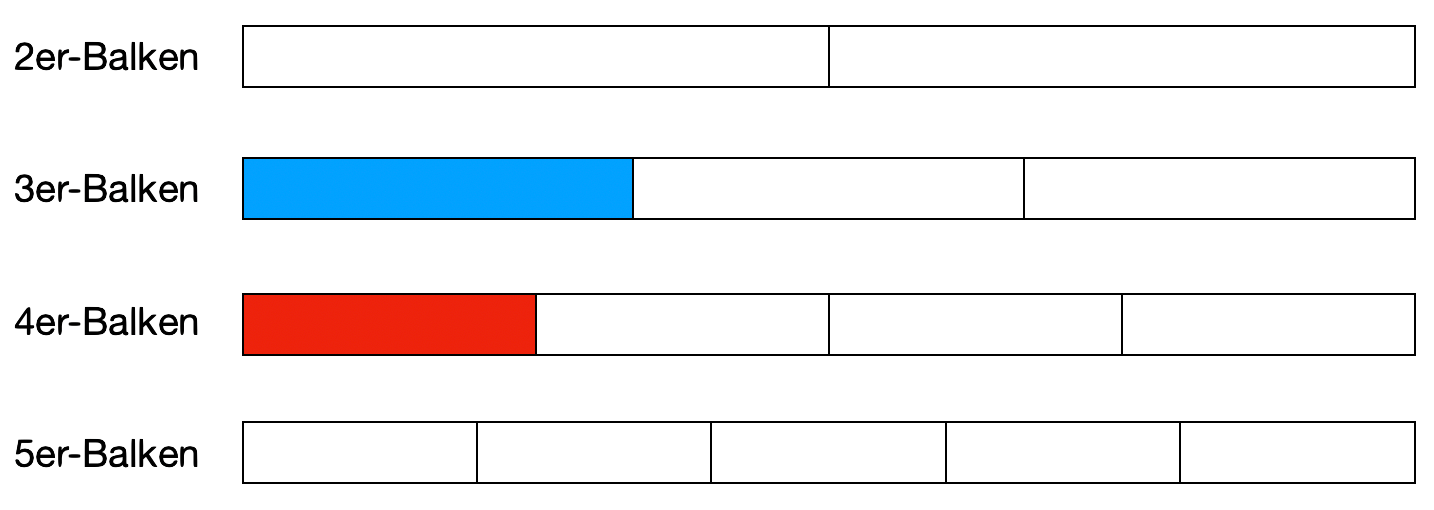
Wie du erkennen kannst ist die blaue Fläche größer als die rote Fläche. $\frac{1}{3}$ ist somit größer als $\frac{1}{4}$.