https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_1-min-1
Winkel zeichnen und messen
Ein Winkel entsteht, wenn zwei Linien sich an einem Punkt schneiden oder von einem gemeinsamen Punkt ausgehen. Der Punkt, an dem sich die Linien treffen, heißt Scheitelpunkt.
Winkel im Alltag
Im täglichen Leben siehst du häufig zwei Linien, die irgendwo aufeinander treffen und somit einen Winkel bilden.
Zum Beispiel bildet die Tür mit der Wand einen Winkel. Öffnest du die Tür, ändert sich der Winkel.
Auch auf Wanduhren siehst du einen Winkel, nämlich zwischen dem Stundenzeiger und dem Minutenzeiger. Je weiter der Stundenzeiger vom Minutenzeiger entfernt ist, desto größer wird der Winkel.
a) 30°
b) 45°
c) 90°
d) 75°
e) 120°
f) 135°
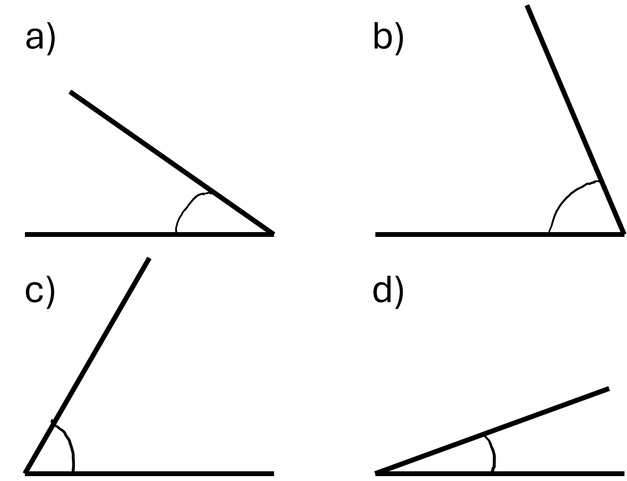
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_1-min-1
Bezeichnung von Winkeln
Winkel werden mit griechischen Buchstaben bezeichnet. Diese Buchstaben sind so ähnlich wie die, die wir sonst verwenden. Aber ein paar Unterschiede gibt es zu beachten.
Wir lernen GRIECHISCH!
In diesem Arbeitsblatt lernst du, wie du die wichtigsten griechischen Buchstaben schreibst. Du brauchst diese immer, wenn du einen Winkel benennen oder beschreiben möchtest.

https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_1-min-1
Arten von Winkeln
Du hast gelernt, wie du Winkel zeichnest, abliest und wie du sie mit griechischen Buchstaben bezeichnest. Hier lernst du, dass Winkel außerdem verschiedene Namen haben. Der Name hängt davon ab, wie groß der Winkel ist.
Name des Winkels
Größe des Winkels
Beispiel
Nullwinkel
exakt 0°
0°
Spitzer Winkel
größer als 0°,
aber kleiner als 90°
45°
Rechter Winkel
exakt 90°
90°
Stumpfer Winkel
größer als 90°,
aber kleiner als 180°
135°
Gestreckter Winkel
exakt 180°
180°
Überstumpfer Winkel
größer als 180°,
aber kleiner als 360°
270°
Vollwinkel
exakt 360°
360°
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_1-min-1
Gemischte Übungen zu Winkeln
Teste im Kreuzworträtsel und in der ANTON App dein Wissen zu Winkeln.
1 | 2 | 3 | 4 | 5 | 6 |
1 | ||||||||||||||
2 | ||||||||||||||
3 | 5 | 4 | 5 | |||||||||||
6 | ||||||||||||||
1 | ||||||||||||||
6 | 2 | 3 | ||||||||||||
4 | ||||||||||||||
7 | ||||||||||||||
- 1Ein rechter Winkel hat genau ... Grad. (Zahlwort)
- 2Zwischen 0° und 90° ist ein ... Winkel.
- 3135° ist ein Beispiel für einen ... Winkel.
- 4Bei exakt 0° spricht man von einem ...
- 5Beträgt ein Winkel 180°, ist dieser Winkel ...
- 6Ein Winkel entsteht, wenn sich zwei ... schneiden.
- 7Ist ein Winkel größer als ein gestreckter Winkel, aber kleiner als ein Vollwinkel, so heißt dieser Winkel ...
Winkel.
Prüfe, ob du alle Übungen und den Test bestehst.
Danach bist du sicher fit für deinen Gelingensnachweis.
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_1-min-1
Bezeichnung von Dreiecken
Bevor wir uns über die Eigenschaften von Dreiecken unterhalten, müssen wir wissen, dass es bestimmte Regeln gibt, wie wir die verschiedenen Teile eines Dreiecks nennen. Das ist wichtig, damit wir alle über dasselbe reden. Es ist also ein bisschen so wie Vokabeln im Englischunterricht.
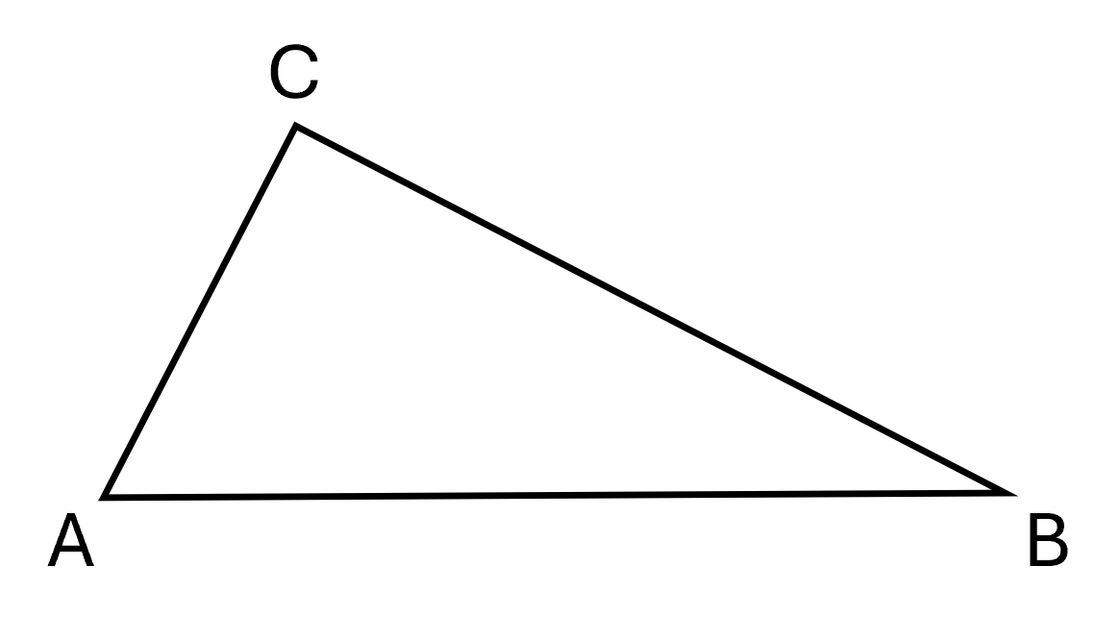
die drei Ecken mit den Großbuchstaben A, B und C. Fange dabei unten links an und gehe gegen den Uhrzeigersinn.
- Großbuchstaben
- gegen den Uhrzeigersinn
- am besten unten links beginnen
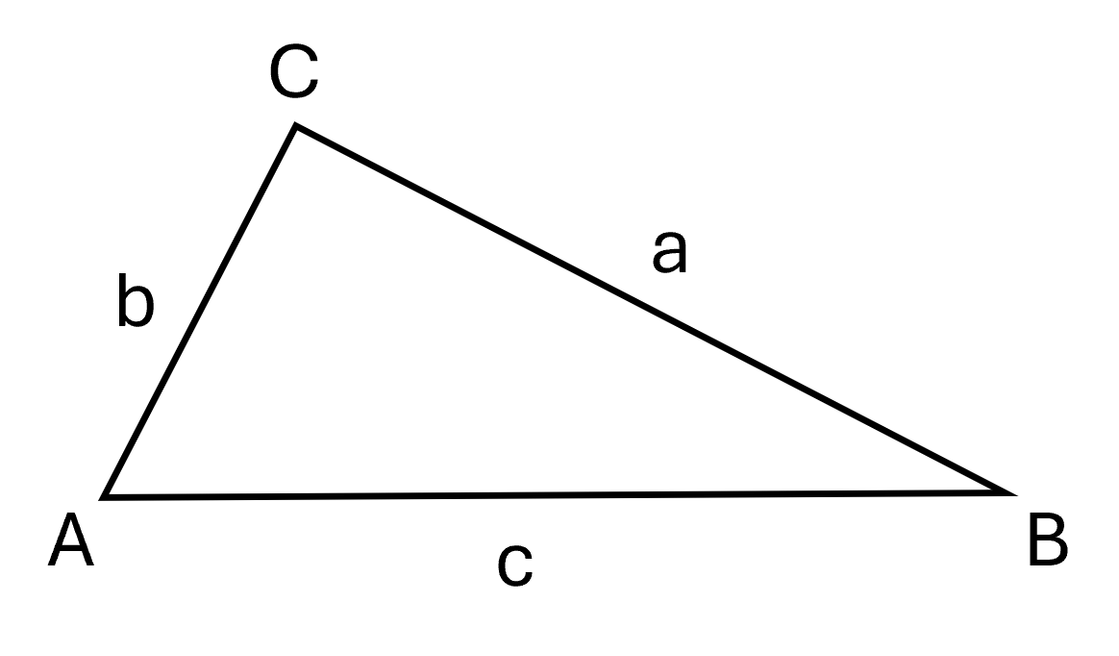
Die Seiten liegen gegenüber der
gleichnamigen Ecke.
- Kleinbuchstaben
- gegenüber der gleichnamigen Ecke
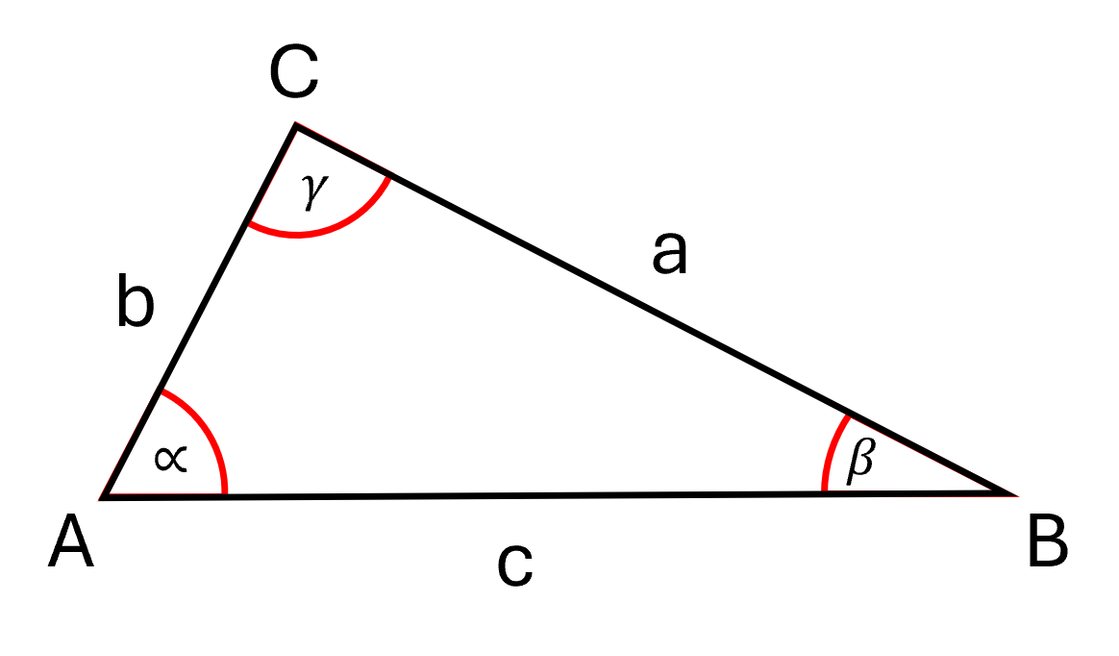
- Griechische Buchstaben
- am gleichnamigen Eckpunkt
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_1-min-1
Dreiecke nach ihren Winkeln unterscheiden

Für diese Seite brauchst du dein Buch Mathematik Heute 7
Auf dieser Seite lernst du, Dreiecke nach ihren Winkeln zu unterscheiden.

Übertrage die Informationen
(2) Innenwinkelsatz für Dreiecke
(3) Einteilung der Dreiecke nach Winkeln
in deinen Hefter.

Wende die Informationen, die du
eben übertragen hast, an.
Löse hierzu Buch S. 137 Nr. 1 und 2.
Berechne bei Nr. 2 zuerst den fehlenden dritten Winkel. Prüfe dann, ob der größte Winkel des Dreiecks spitzwinklig, rechtwinklig oder stumpfwinklig ist.
(--> 1_Dreiecke_1_Winkel_Min_Aufg)
a) stumpfwinklig ist.
b) spitzwinklig ist.
c) rechtwinklig ist.
Du möchtest in den Aufgaben weniger Text (größer als
, kleiner als
, genauso groß wie
) schreiben? Hierfür gibt es in Mathe drei wichtige Zeichen, die genau das ausdrücken und dir somit viel Zeit und Mühe sparen:
< bedeutet kleiner als
, z. B. 1 < 2 (sprich: eins ist kleiner als zwei
).
= bedeutet gleich
, z. B. 4 = 4 (sprich: vier ist gleich vier)
> bedeutet größer als
, z. B. 10 > 5 (sprich: zehn ist größer als fünf
).
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_1-min-1
Dreiecke nach ihren Seiten unterscheiden

Für diese Seite brauchst du dein Buch Mathematik Heute 7
Auf dieser Seite lernst du, Dreiecke nach ihren Winkeln zu unterscheiden.

Übertrage die Informationen
(3) Ordnen der Dreiecke nach Seiten
in deinen Hefter.
Bei einem gleichschenkligen Dreieck sind zwei Seiten gleich lang. Diese Seiten nennt man Schenkel. Die dritte Seite heißt Basis. Die beiden Winkel zwischen der Basis und den beiden Schenkeln sind gleich groß.
Bei einem gleichseitigen Dreieck sind alle drei Seiten gleich lang. Auch alle Winkel sind gleich groß, und zwar 60°.
Der Grund liegt in der Innenwinkelsumme, denn 180° : 3 = 60°.
Alle anderen Dreiecke heißen unregelmäßig
. Sie haben drei unterschiedlich lange Seiten und drei unterschiedlich große Winkel.
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_1-min-1
Gemischte Übungen zu den Eigenschaften von Dreiecken
Winkel in Dreiecken.
Starte die Übungen
Aussagen vervollständigen und
Winkel berechnen (1).
a) gleichseitig, gleichschenklig oder unregelmäßig sind.
b) spitzwinklig, rechtwinklig oder stumpfwinklig sind.

a) spitzwinkliges Dreieck
b) stumpfwinkliges Dreieck
c) gleichschenkliges Dreieck
d) rechtwinkliges Dreieck
e) unregelmäßiges Dreieck
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_1-min-1
unterscheiden.
unterscheiden.
Wenn du wenigstens 4 der 5 Kreuze bei sehr gut
oder gut
gesetzt hast, ist es vielleicht langsam Zeit für den Gelingensnachweis. Wenn noch 2 oder mehr Kreuze bei nicht so gut
oder überhaupt nicht gut
stehen, solltest du dir diesen Teil lieber nochmal anschauen.
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_1-min-1


