https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_2-reg
Im Regelstandard wird das Wissen aus dem
Minimalstandard vorausgesetzt. Solltest du also bei den folgenden Aufgaben Probleme haben (z. B. beim Nutzen des Geodreiecks, beim Schreiben griechischer
Buchstaben), blättere nochmal zurück zum
Minimalstandard.
Das gilt insbesondere für die korrekte Beschriftung von Dreiecken!
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_2-reg
Winkelbeziehungen Teil 1: Zwei sich schneidende Geraden
Auf diesem Arbeitsblatt wirst du Winkel zeichnen und dabei einiges über sie lernen. Versprochen!
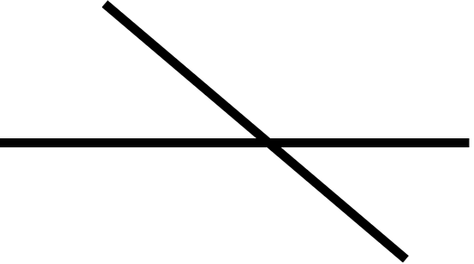
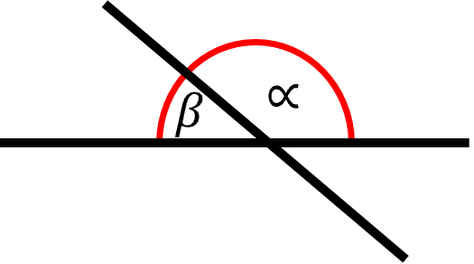
Wenn sich zwei Geraden schneiden, sind zwei benachbarte Winkel ...
Fahre mit den folgenden Aufgaben erst fort, wenn du deine Vermutung fertig notiert hast.
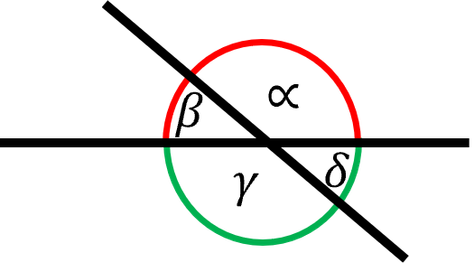
Wenn sich zwei Geraden schneiden, sind zwei gegenüberliegende Winkel ...
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_2-reg
Du hast in den Arbeitsschritten (1) bis (11) zwei wichtige Winkelbeziehungen herausgefunden. Sie nennen sich Nebenwinkel und Scheitelwinkel.
Wenn sich zwei Geraden schneiden, sind zwei benachbarte Winkel zusammen immer 180°.
Mathematisch ausgedrückt: α + β = 180°.
Man nennt diese benachbarten Winkel Nebenwinkel.
Wenn sich zwei Geraden schneiden, sind zwei gegenüberliegende Winkel immer gleich groß.
Mathematisch ausgedrückt: α = β.
Man nennt diese gegenüberliegenden Winkel Scheitelwinkel.
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_2-reg
Winkelbeziehungen Teil 2: Eine Gerade durch zwei parallele Geraden
Bislang hast du kennengelernt, was passiert, wenn sich zwei Geraden schneiden. Hier lernst du, was passiert, wenn eine Gerade zwei andere Geraden schneidet. Doch ganz langsam der Reihe nach.
parallel?
Zwei Geraden sind
parallel, wenn sie in
gleicher Richtung und in gleichem Abstand neben-einander verlaufen.
Man nennt diese Winkel Stufenwinkel.
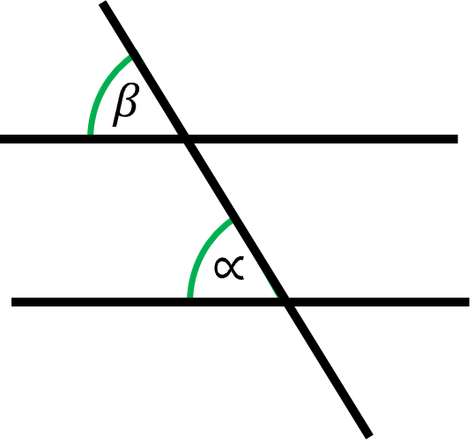
Stufenwinkel entstehen, wenn ...
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_2-reg
Fahre mit den folgenden Aufgaben erst fort, wenn du deine Vermutung auf der vorherigen Seite fertig notiert hast.
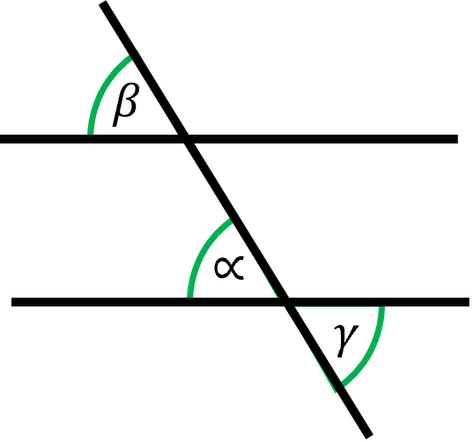
Es sollte also jetzt ungefähr so aussehen:
Man nennt die Winkel γ und β Wechselwinkel.
Wechselwinkel entstehen, wenn ...
Du hast in den Arbeitsschritten (1) bis (9) zwei weitere wichtige Winkelbeziehungen herausgefunden. Sie nennen sich Stufenwinkel und Wechselwinkel.
Stufenwinkel entstehen, wenn zwei parallele Geraden von einer dritten Geraden geschnitten werden. Dabei sind Stufenwinkel die Winkel, welche auf der gleichen Seite der Schnittgeraden und auf der gleichen Seite der Parallelen liegt.
Zwei Stufenwinkel sind immer gleich groß.
Wechselwinkel entstehen, wenn zwei parallele Geraden von einer dritten Geraden geschnitten werden. Dabei sind Wechselwinkel die Winkel, welche auf der unterschiedlichen Seiten der Schnittgeraden und auf unterschiedlichen Seiten der Parallelen liegt.
Zwei Wechselwinkel sind immer gleich groß.
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_2-reg
Winkelbeziehungen: Gemischte Übungen
Wenn sich Linien schneiden, entsteht nicht nur ein Winkel, sondern mehrere Winkel. Es spart Zeit und ermöglicht neue Überlegungen, wenn man ein bisschen über diese Winkel und ihre Beziehungen zueinander weiß.
Alles schon gewusst? Super!
Wenn sich zwei Geraden schneiden, entstehen Winkel.
Zwei Winkel, die nebeneinander liegen, heißen . Sie sind zusammen immer ° groß, da sie gemeinsam einen gestreckten Winkel bilden. Ein Beispiel: α und β seien Nebenwinkel. Der Winkel α sei 100° groß. Dann ist der Winkel β = °,
denn es gilt: α β=180°.
Zwei Winkel, die gegenüber liegen, nennt man . Sie sind immer groß. Ein Beispiel: α und β seien Scheitelwinkel. Der Winkel α sei 75° groß. Dann ist der Winkel β = °, denn es gilt: α β.
(auf der nächsten Seite geht es weiter)
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_2-reg
Wenn wir sogar drei Geraden haben, entstehen Wechselwinkel und Stufenwinkel. Dafür müssen zwei Geraden sein und die dritte
Gerade die anderen beiden schneiden.
Wechselwinkel und Stufenwinkel haben noch eine weitere Gemeinsamkeit, aber natürlich auch einen Unterschied. Die Gemeinsamkeit ist, dass sowohl zwei Wechselwinkel als auch zwei Stufenwinkel immer groß sind.
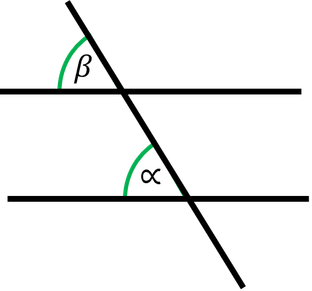
Der Unterschied ist in ihrer Lage. Zwei Winkel, die auf der selben Seite der parallelen Geraden und auf der selben Seite der schrägen, schneidenden
Geraden liegen (siehe Bild), heißen .
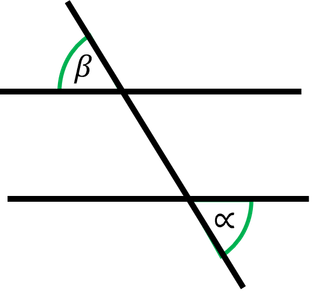
Zwei Winkel, die hingegen auf unterschiedlichen Seiten der parallelen Geraden und auf unterschiedlichen Seiten der schrägen, schneidenden
Geraden liegen (siehe Bild), heißen .
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_2-reg
- Markiere einen Winkel zwischen den zwei Geraden.
- Zeichne eine erste Gerade.
- Markiere nun einen zweiten Winkel, der direkt daneben liegt. Bezeichne ihn mit β.
- Bezeichne den ersten Winkel mit α.
- Zeichne eine zweite Gerade, welche die erste Gerade schneidet.
- Die beiden markierten Winkel sind die Nebenwinkel. Sie ergeben zusammen 180°.
a) geg: α und β sind Scheitelwinkel, β = 75°
ges.: α
b) geg: α und β sind Nebenwinkel, β = 65°
ges.: α
c) geg: α und β sind Stufenwinkel, β = 18°
ges.: α
d) geg: α und β sind Scheitelwinkel, β = 125°
ges.: α
e) geg: α und β sind Wechselwinkel, β = 65°
ges.: α
f) geg: α und β sind Nebenwinkel, β = 165°
ges.: α
g) geg: α und β sind Nebenwinkel, β = 100°
ges.: α
h) geg: α und β sind Wechselwinkel, β = 90°
ges.: α
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_2-reg
Wiederholung: Winkel und Seitenlängen von Dreiecken
Du hast in den Arbeitsmaterialien zum Mindeststandard gelernt, Dreiecke nach ihren Winkeln und Seitenlängen zu unterscheiden. Bevor du weitere Eigenschaften kennenlernst, prüfe dein bis hierhin erlerntes Wissen mit den folgenden Aufgaben.

Prüfe die Aussagen der Schülerinnen und Schüler im Bild. Fertige hierfür zu jeder Aussage eine Zeichnung eines Dreiecks an, um zu beantworten, ob die Aussage wahr oder falsch ist.
Schreibe anschließend eine kurze Begründung zu jeder Antwort.
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_2-reg
Du hast im Mindeststandard auch schon weitere Eigenschaften von Dreiecken kennengelernt, z. B. dass die Innenwinkel zusammen immer 180° ergeben.
Es gibt aber noch weitere Eigenschaften, die du kennen solltest. Diese beziehen sich auf die Seitenlängen von Dreiecken.
Symmetrie
Einige Dreiecke sind achsensymmetrisch (auch spiegelsymmetrisch genannt). Dabei gilt:
Gleichseitige Dreiecke haben genau drei
Symmetrieachsen (jeweils von einer Ecke zur Mitte der gegenüberliegenden Seite)
Gleichschenklige Dreiecke haben genau eine Symmetrieachse (vom Winkel an der Spitze zur Mitte der Basisseite)
Unregelmäßige Dreiecke haben keine Symmetrieachse
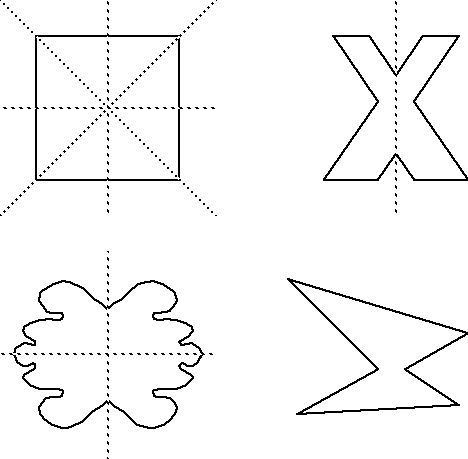
Eine Figur (z. B. ein Dreieck) ist achsensymmetrisch, wenn du sie an einer Symmetrieachse spiegeln kannst. Danach muss die gespiegelte Hälfe gleich aussehen wie die erste Hälfe. Daher nennt man die Achsensymmetrie auch Spiegelsymmetrie.
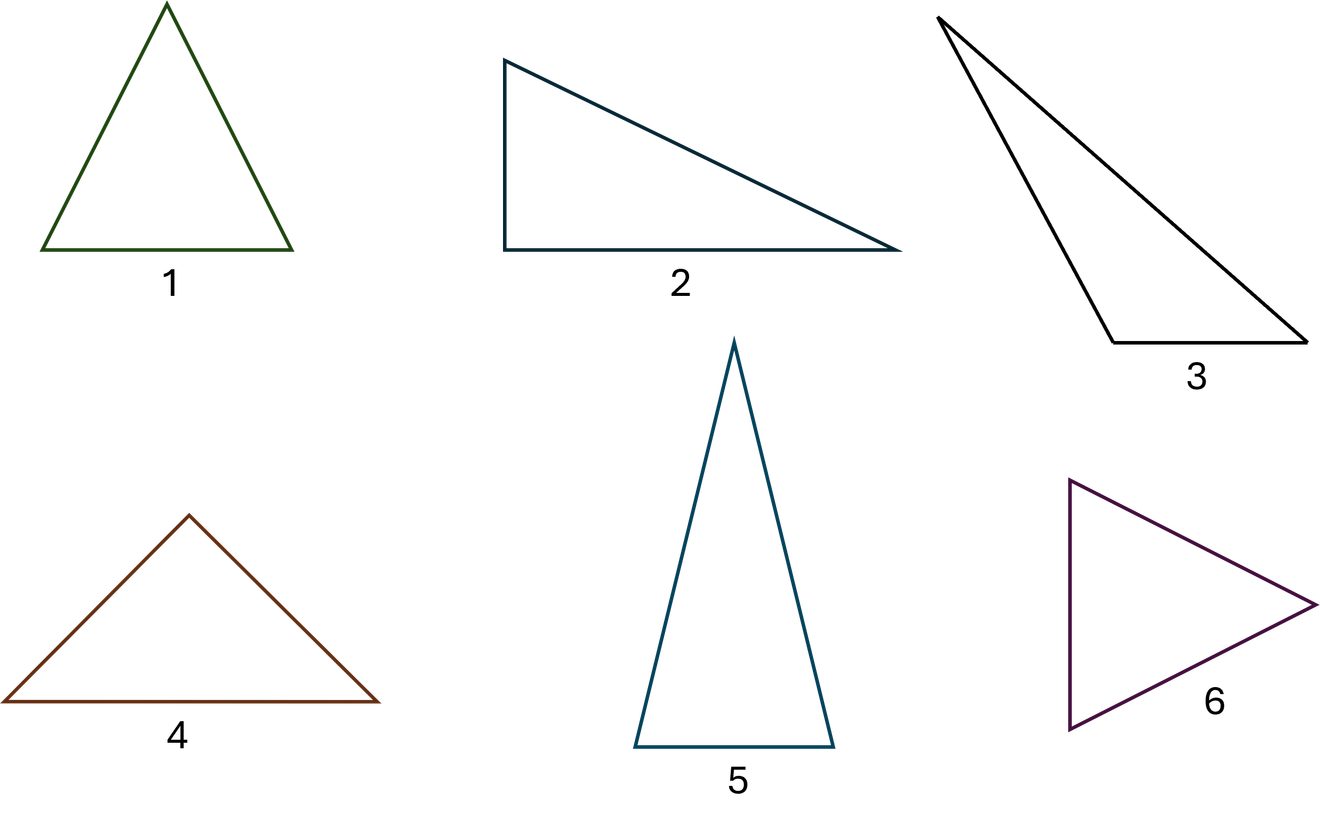
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_2-reg
Dreiecks-Ungleichung
Nimm dir jeweils drei dieser Gegenstände und versuche, aus ihnen ein Dreieck zu legen. Mit welchen Gegenständen funktioniert es, mit welchen nicht? Formuliere eine Vermutung zu den Seitenlängen, damit ein Dreieck existieren kann. Du darfst dafür den Satzanfang nutzen:
Ein Dreieck kann nur dann existieren, wenn die Länge von zwei Seiten ...
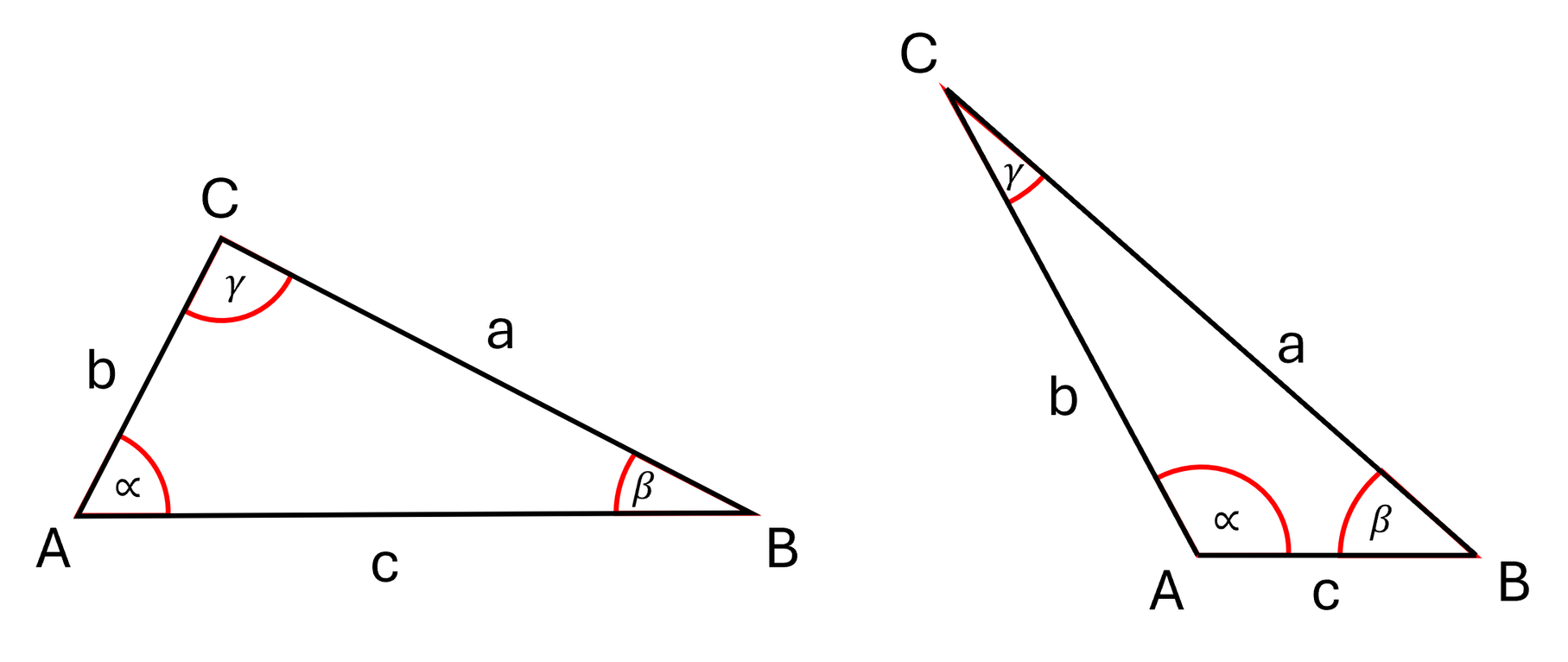
Seiten-Winkel-Beziehung im Dreieck
Zeichne dann ein drittes, eigenes Dreieck und fertige auch für dieses Dreieck eine solche Tabelle an. Betrachte dann die Seitenlängen und die Winkelgrößen. Was fällt dir auf? Formuliere deine Vermutung!
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_2-reg

Hast du in Aufgabe (2) und (3) eine Vermutung formuliert. Dann öffne jetzt dein Buch und vergleiche deine Vermutungen mit den beiden Informationen unten auf der Seite.
Waren deine Vermutungen nicht korrekt? Dann übertrage die beiden Merkinhalte (
Seiten-Winkel-Beziehung im Dreieck und
Dreiecksungleichung) in dein Heft.
Wenn du wenigstens 5 der 6 Kreuze bei sehr gut
oder gut
gesetzt hast, ist es vielleicht langsam Zeit für den Gelingensnachweis. Wenn noch 2 oder mehr Kreuze bei nicht so gut
oder überhaupt nicht gut
stehen, solltest du dir diesen Teil lieber nochmal anschauen.
https://editor.mnweg.org/entdecken/dokument/1-dreiecke_1-winkeleigenschaften_2-reg


