Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
1. Strahlensatz Verhältnisse
Mathematik Flächen R 9
1
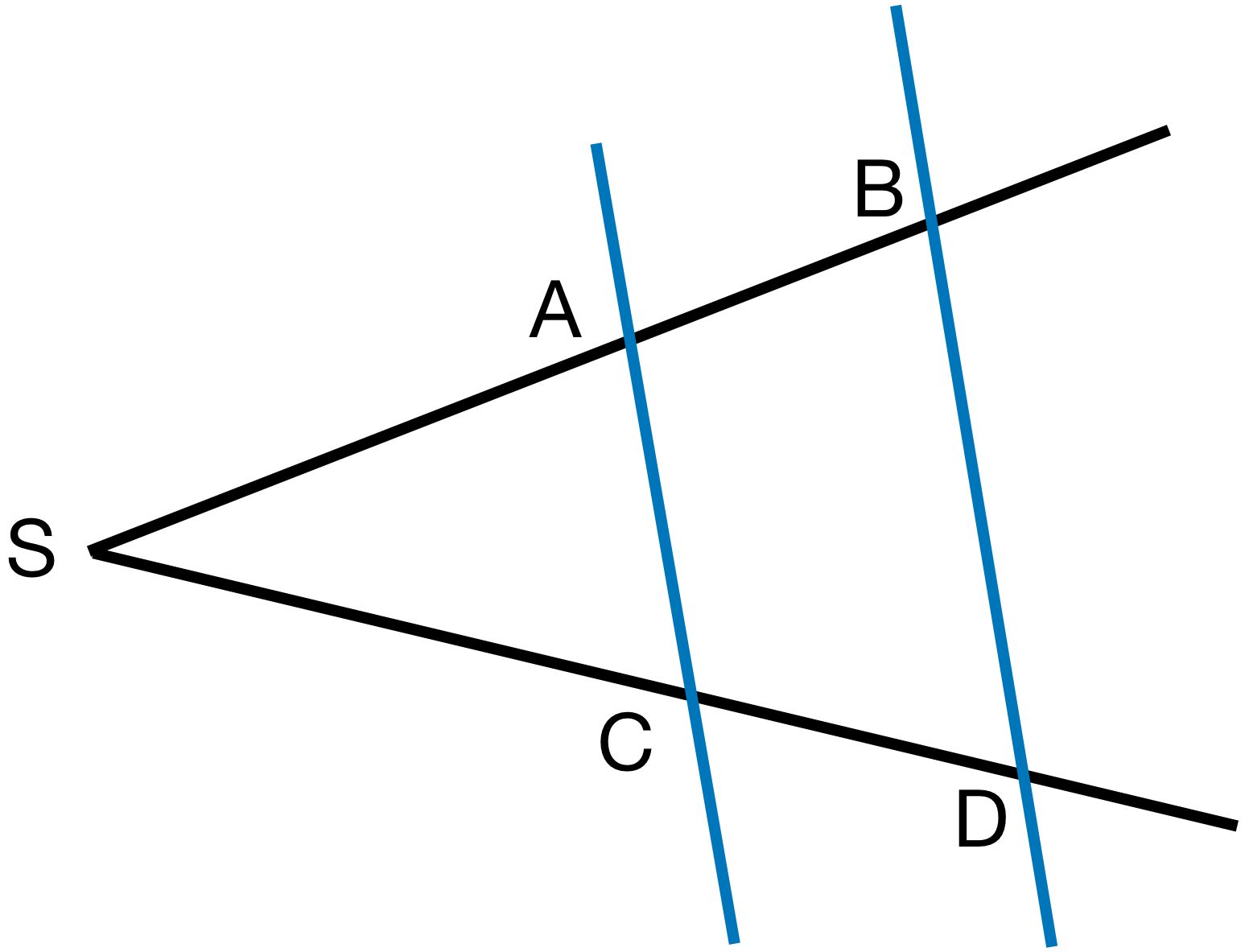
Kreuze die richtigen Verhältnisse an! Es können auch mehrere Verhältnisse richtig sein.
richtig | falsch |
|
|
|
|
|
|
SASB = SCSD
SCSA = SASB
CDAB = SCSA
richtig | falsch |
|
|
|
|
|
|
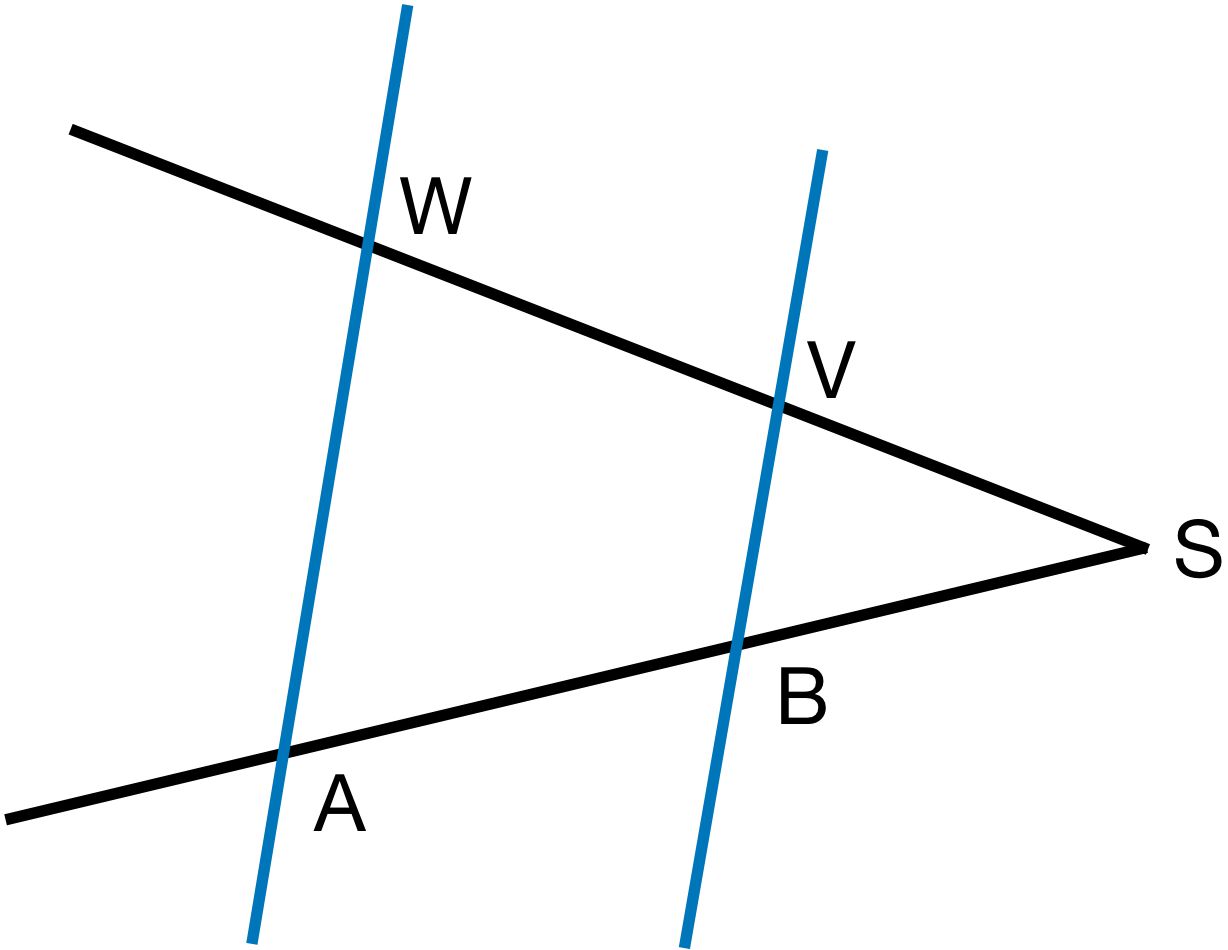
SBSV = VWAB
SBSV = ABVW
SBSA = SWSV
2
Ergänze die Verhältnisse und finde 5 weitere Verhältnisse!
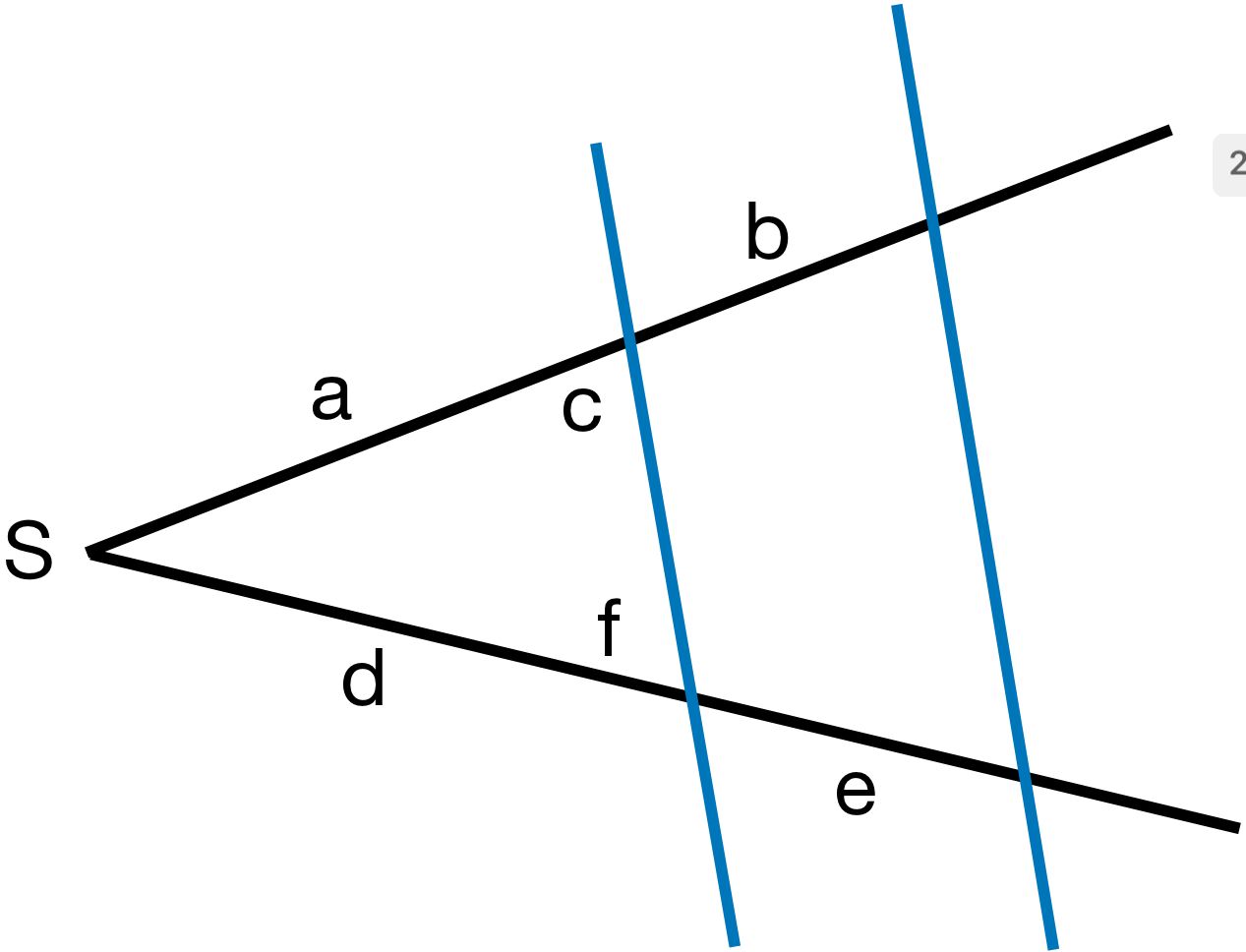

- ad=e
- ab=c
- cb=e
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/137daf16
https://editor.mnweg.org/entdecken/dokument/137daf16


