Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
Bruchteile von Längen
Mathematik Bruchrechnen R 5
1
Berechne den angegebenen Bruchteil.
b) 43 m = cm
d) 21 m = dm
f) 63 m = cm
h) 53 km = m
j) 104 m = cm
l) 205 km = cm
a) 21 km = m
c) 51 cm = mm
e) 54 m = cm
g) 41 m = cm
i) 101 m = cm
k) 201 m = cm
2
Welcher Bruchteil ist eingefärbt?
Schreibe links den richtigen Bruch hin. Schreibe rechts hin, wie viel das in der vorgegebenen Einheit ist. Bsp: 41 km = 250 m
Schreibe links den richtigen Bruch hin. Schreibe rechts hin, wie viel das in der vorgegebenen Einheit ist. Bsp: 41 km = 250 m

a)
21
km = m

b)
43
m = cm
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/14c2a31d
https://editor.mnweg.org/entdecken/dokument/14c2a31d
AB
Bruchteile von Längen
Mathematik Bruchrechnen R 5

c)
52
km = m
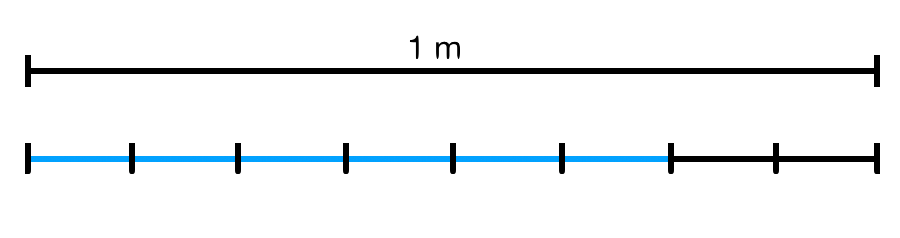
d)
86
m = cm
3
Stelle die Längenangabe als Anteil dar!
a) 250 m = 41 km
c) 100 m = 101 km
e) 2 mm = 51 cm
g) 50 cm = 21 m
i) 2 dm = 51 m
b) 200 m = 51 km
d) 800 m = 108 km
f) 8 dm = 54 m
h) 125 m = 81 km
j) 300 m = 103 km
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/14c2a31d
https://editor.mnweg.org/entdecken/dokument/14c2a31d


