HerunterladenAls PDF Herunterladen
  • Grundaufgaben Pythagoras 2
  • Deliah Herbstritt
  • 21.07.2020
  • Mathematik
  • Flächen
  • R
  • 9
  • Einzelarbeit
  • Arbeitsblatt
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
Grundaufgaben Pythagoras 2
Mathematik Flächen R 9
1
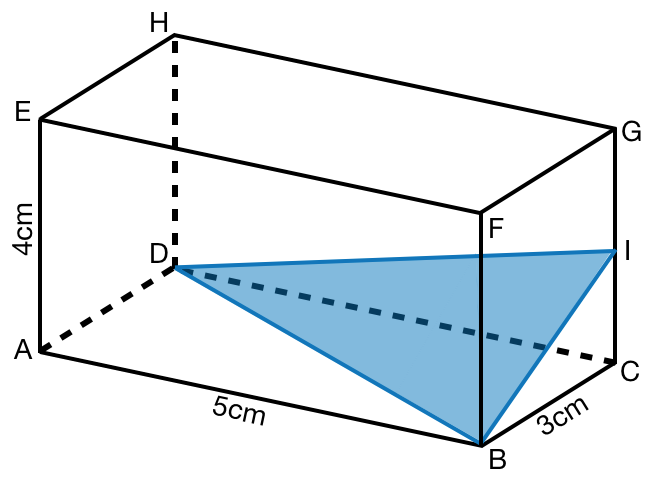
Der Punkt I liegt auf hal­ber Höhe der Stre­cke CG‾\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \overline{CG}.
Be­rech­ne den Um­fan­ge des Drei­eckes DBI.
Lösung1
Flä­chen­dia­go­na­le BD‾\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \overline{BD}:
b2=(5cm)2+(3cm)2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} b^2=(5cm)^2+(3cm)^2
b2=25cm+9cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} b^2=25cm+9cm
b2=34cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} b^2=34cm
b2=5,83cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} b^2=\sqrt{5{,}83cm}
b≈5,83cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} b\approx5{,}83cm

Flä­chen­dia­go­na­le BI‾\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \overline{BI}:
i2=(3cm)2+(2cm)2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} i^2=(3cm)^2+(2cm)^2
i2=9cm+4cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} i^2=9cm+4cm
i2=13cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} i^2=13cm
i2=13cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} i^2=\sqrt{13cm}
i≈3,60cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} i\approx3{,}60cm


Raum­dia­go­na­le DI‾\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \overline{DI}:
d2=(5,83cm)2+(3,6cm)2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} d^2=(5{,}83cm)^2+(3{,}6cm)^2
d2=33,99cm+12,96cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} d^2=33{,}99cm+12{,}96cm
d2=46,95cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} d^2=46{,}95cm
d2=46,95cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} d^2=\sqrt{46{,}95cm}
d≈6,85cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} d\approx6{,}85cm

Um­fang (alle Sei­ten­län­gen des Drei­ecks):
U=5,83cm+3,60cm+6,85cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} U=5{,}83cm+3{,}60cm+6{,}85cm
U=16,28cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} U=16{,}28cm

Ant­wort: Der Um­fang des Drei­ecks be­trägt ca. 16,28cm.
Bereitgestellt von: Deliah Herbstritt Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/23347ba0
Seite: 1/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/23347ba0
AB
Grundaufgaben Pythagoras 2
Mathematik Flächen R 9
2
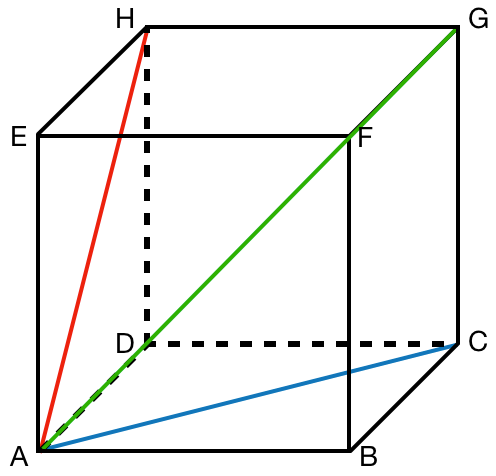
Dia­go­na­len im Wür­fel
  • Zeich­ne das Schräg­bild eines Wür­fels mit der Kan­ten­län­ge 5cm.
  • Zeich­ne und mar­kie­re die drei Dia­go­na­len far­big wie in der Ab­bil­dung.
  • Be­nen­ne die far­bi­gen Dia­go­na­len.
  • Be­rech­ne die Ge­samt­län­ge der drei far­bi­gen Dia­go­na­len.
Lösung2
c)
rote Dia­go­na­le = Raum­dia­go­na­le
grüne Dia­go­na­le = Flä­chen­dia­go­na­le
blaue Dia­go­na­le = Grund­flä­chen­dia­go­na­le

d)
Grund­flä­chen­dia­go­na­le:
i2=a2+b2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} i^2=a^2+b^2
i2=(5cm)2+(5cm)2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} i^2=(5cm)^2+(5cm)^2
i2=25cm+25cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} i^2=25cm+25cm
i2=50cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} i^2=50cm
i2=50cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} i^2=\sqrt{50cm}
i≈7,07cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} i^\approx7{,}07cm

Ant­wort: Die Grund­flä­chen­dia­go­na­le be­trägt 7,07cm.

Raum­dia­go­na­le:
j2=i2+b2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} j^2=i^2+b^2
j2=(7,07cm)2+(5cm)2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} j^2=(7{,}07cm)^2+(5cm)^2
j2=50cm+25cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} j^2=50cm+25cm
j2=75cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} j^2=75cm
j2=75cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} j^2=\sqrt{75cm}
j2≈8,66cm\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} j^2\approx8{,}66cm

Ant­wort: Die Raum­dia­go­na­le be­trägt 8,66cm.

Flä­chen­dia­go­na­le:

Ant­wort: Die Flä­chen­dia­go­na­le ist bei einem Wür­fel gleich der Grund­flä­chen­dia­go­na­le.
Diese be­trägt 7,07cm.
Bereitgestellt von: Deliah Herbstritt Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/23347ba0
Seite: 2/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/23347ba0
x