HerunterladenAls PDF Herunterladen
  • Formeln umstellen
  • P. Ruppaner
  • 21.07.2020
  • Mathematik
  • Flächen
  • M
  • 9
  • Einzelarbeit
  • Arbeitsblatt
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
Formeln umstellen
Mathematik Flächen M 9
1
Stel­le auf den Satz des Py­tha­go­ras so um, wie du es auf dem INFO-​Blatt be­reits ge­lernt hast. Stel­le drei For­meln für die Be­rech­nung der Hy­po­te­nu­se und für die Be­rech­nung der bei­den Ka­the­ten auf.
Lösung1
Be­rech­nung der Hy­po­te­nu­se c\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} c:
c2=a2+b2∣ \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} c^2=a^2+b^2\qquad|\sqrt{\nobreakspace}

c=a2+b2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} c = \sqrt{a^2+b^2}

Be­rech­nung der Ka­the­te a\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} a:

a2+b2=c2 ∣−b2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} a^2+b^2 = c^2\qquad\qquad\nobreakspace|-b^2

 a2=c2−b2∣ \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \nobreakspace\qquad a^2=c^2-b^2\qquad|\sqrt{\nobreakspace}

  a=c2−b2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \qquad\nobreakspace\nobreakspace a = \sqrt{c^2-b^2}

Be­rech­nung der Ka­the­te b\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} b:

b2+a2=c2 ∣−a2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} b^2+a^2 = c^2\qquad\qquad\nobreakspace|-a^2

 b2=c2−a2∣ \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \nobreakspace\qquad b^2=c^2-a^2\qquad|\sqrt{\nobreakspace}

  b=c2−a2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \qquad\nobreakspace\nobreakspace b = \sqrt{c^2-a^2}
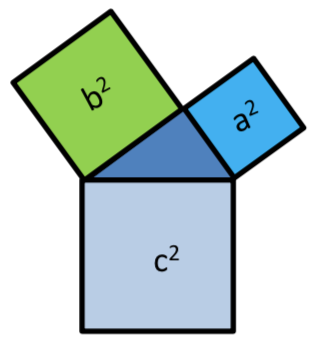
Be­nen­nung der Sei­ten

Die Namen der Sei­ten müs­sen nicht immer nur a, b und c sein, son­dern kön­nen jeden be­lie­bi­gen Buch­sta­ben haben.

Falls du das Thema noch nicht ver­stan­den hat kannst du dir das INFO-​Blatt noch ein­mal durch­le­sen

Bereitgestellt von: P. Ruppaner Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/2cf68ac2
Seite: 1/4
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/2cf68ac2
AB
Formeln umstellen
Mathematik Flächen M 9
2
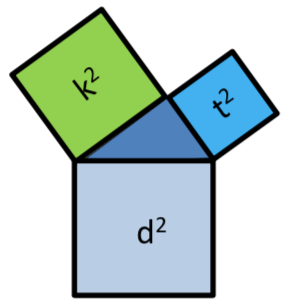
Stel­le drei For­meln für die Be­rech­nung der Hy­po­te­nu­se und für die Be­rech­nung der bei­den Ka­the­ten auf.
Lösung2
Be­rech­nung der Hy­po­te­nu­se d\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} d:
d2=t2+k2∣ \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} d^2=t^2+k^2\qquad|\sqrt{\nobreakspace}

d=t2+k2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} d = \sqrt{t^2+k^2}

Be­rech­nung der Ka­the­te t\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} t:

t2+k2=d2 ∣−k2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} t^2+k^2 = d^2\qquad\qquad\nobreakspace|-k^2

 t2=d2−k2∣ \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \nobreakspace\qquad t^2=d^2-k^2\qquad|\sqrt{\nobreakspace}

  t=d2−k2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \qquad\nobreakspace\nobreakspace t = \sqrt{d^2-k^2}

Be­rech­nung der Ka­the­te k\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} k:

k2+t2=d2 ∣−t2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} k^2+t^2 = d^2\qquad\qquad\nobreakspace|-t^2

 k2=d2−t2∣ \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \nobreakspace\qquad k^2=d^2-t^2\qquad|\sqrt{\nobreakspace}

  k=d2−t2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \qquad\nobreakspace\nobreakspace k = \sqrt{d^2-t^2}
Bereitgestellt von: P. Ruppaner Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/2cf68ac2
Seite: 2/4
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/2cf68ac2
AB
Formeln umstellen
Mathematik Flächen M 9
3
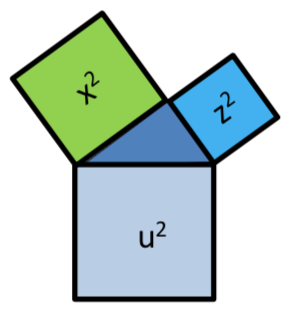
Stel­le drei For­meln für die Be­rech­nung der Hy­po­te­nu­se und für die Be­rech­nung der bei­den Ka­the­ten auf.
Lösung3
Be­rech­nung der Hy­po­te­nu­se u\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} u:
u2=z2+x2∣ \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} u^2=z^2+x^2\qquad|\sqrt{\nobreakspace}

u=z2+x2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} u = \sqrt{z^2+x^2}

Be­rech­nung der Ka­the­te z\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} z:

z2+x2=u2 ∣−x2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} z^2+x^2 = u^2\qquad\qquad\nobreakspace|-x^2

 z2=u2−x2∣ \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \nobreakspace\qquad z^2=u^2-x^2\qquad|\sqrt{\nobreakspace}

  z=u2−x2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \qquad\nobreakspace\nobreakspace z = \sqrt{u^2-x^2}

Be­rech­nung der Ka­the­te x\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} x:

x2+z2=u2 ∣−z2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} x^2+z^2 = u^2\qquad\qquad\nobreakspace|-z^2

 x2=u2−z2∣ \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \nobreakspace\qquad x^2=u^2-z^2\qquad|\sqrt{\nobreakspace}

  x=u2−z2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \qquad\nobreakspace\nobreakspace x = \sqrt{u^2-z^2}
Bereitgestellt von: P. Ruppaner Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/2cf68ac2
Seite: 3/4
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/2cf68ac2
AB
Formeln umstellen
Mathematik Flächen M 9
4
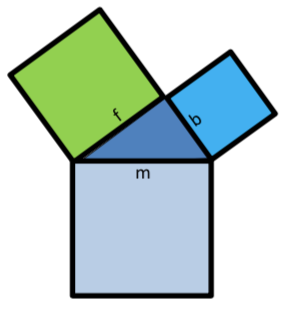
Stel­le drei For­meln für die Be­rech­nung der Hy­po­te­nu­se und für die Be­rech­nung der bei­den Ka­the­ten auf.
Lösung4
Be­rech­nung der Hy­po­te­nu­se u\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} u:
u2=z2+x2∣ \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} u^2=z^2+x^2\qquad|\sqrt{\nobreakspace}

u=z2+x2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} u = \sqrt{z^2+x^2}

Be­rech­nung der Ka­the­te z\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} z:

z2+x2=u2 ∣−x2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} z^2+x^2 = u^2\qquad\qquad\nobreakspace|-x^2

 z2=u2−x2∣ \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \nobreakspace\qquad z^2=u^2-x^2\qquad|\sqrt{\nobreakspace}

  z=u2−x2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \qquad\nobreakspace\nobreakspace z = \sqrt{u^2-x^2}

Be­rech­nung der Ka­the­te x\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} x:

x2+z2=u2 ∣−z2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} x^2+z^2 = u^2\qquad\qquad\nobreakspace|-z^2

 x2=u2−z2∣ \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \nobreakspace\qquad x^2=u^2-z^2\qquad|\sqrt{\nobreakspace}

  x=u2−z2\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \qquad\nobreakspace\nobreakspace x = \sqrt{u^2-z^2}
Bereitgestellt von: P. Ruppaner Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/2cf68ac2
Seite: 4/4
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/2cf68ac2
x