Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
Schaubild und Funktionsgleichung
So kannst du vom Schaubild einer linearen Funktion die passende Funktionsgleichung ablesen:
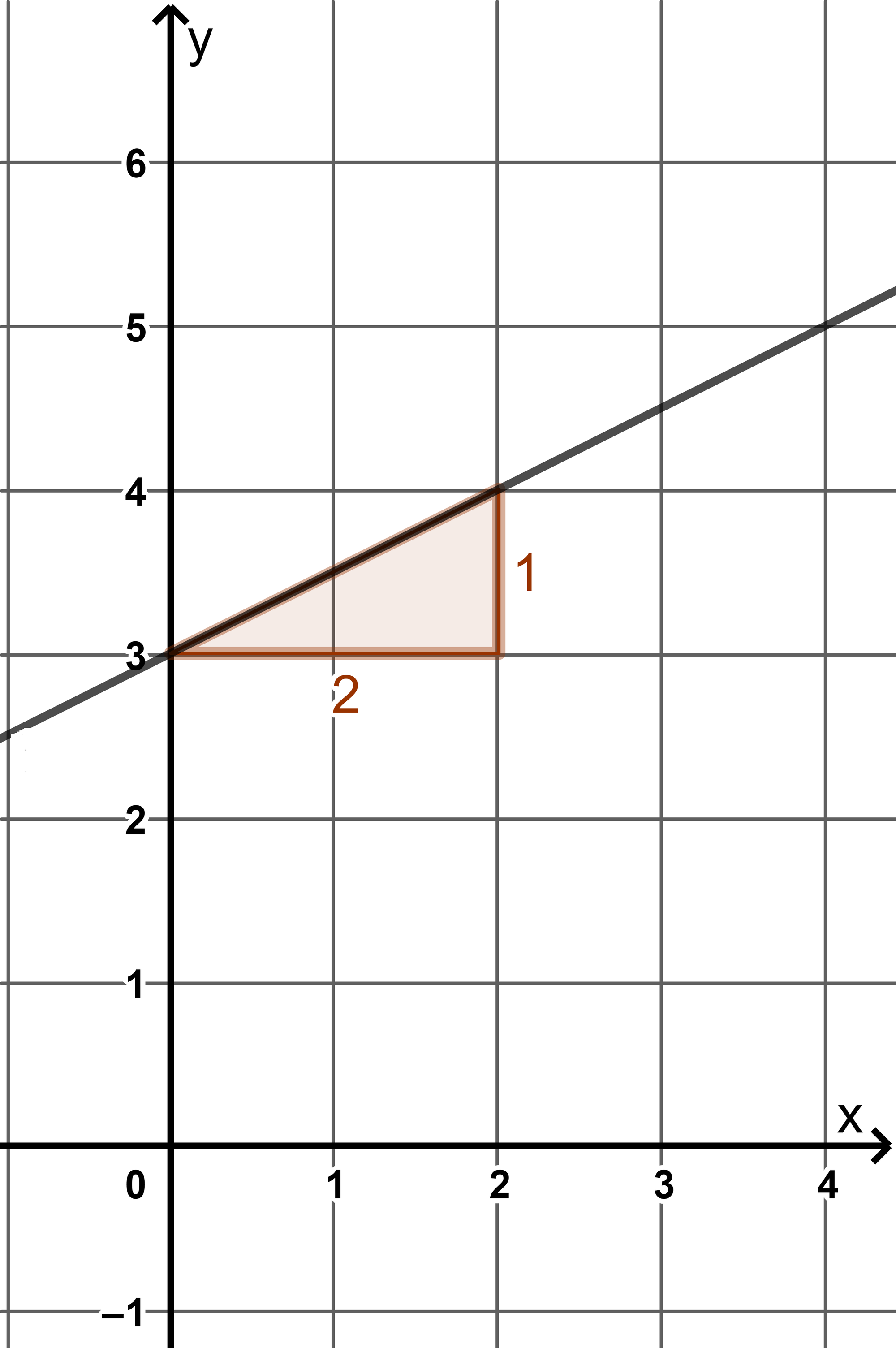
1) Finde die Größe des y-Achsenabschnitts c heraus. (Das sieht man am Schnittpunkt des Graphen mit der y-Achse!) In Abb. 1 ist er 3.
2) Wo schneidet der Funktionsgraph die nächste Koordinatenkreuzung? - Im Beispiel bei (2|4).
Von dort zeichne das Steigungsdreieck zum y-Achsenabschnitt.
3) Nun kannst du die Steigung m als Bruchzahl ablesen. (Die x-Schritte kommen in den Nenner, die y-Schritte in den Zähler des Bruchs). In Abb. 1 sind das 2 Schritte parallel zur x-Achse und 1 Schritt parallel zur y-Achse.
4) Schreibe die Funktionsgleichung auf in der Form y = mx + c. Für Abb.1 steht sie hier rechts vom Kasten:
1
1
Verfahre nach der Anleitung oben und markiere die richtige Funktionsgleichung zu Abb. 2.
2
Vergiss nicht, das Steigungsdreieck einzuzeichnen. Welche Funktionsgleichung passt zu Abb. 3?
2
3
