Kürzen = Vergröbern
Kürzen kann man als eine Art Vergröbern sehen. Am Besten sieht man das an der Balkentafel:
Nehmen wir den Bruch 93 als Beispiel. Die eingefärbte Fläche von 93 in einem 9er-Balken kann man durch 3 teilen und man erhält die gleich große Fläche in einem 3er-Balken.
Generell ist beim Vergröbern jedoch Vorsicht geboten: Man kann einen Bruch nur vergröbern bzw. kürzen, wenn man sowohl Zähler, als auch Nenner durch die gleiche Zahl dividieren kann und man dabei wieder eine ganze Zahl erhält. Beispielsweise den Zähler von91, also die 1, kann man zwar durch 3 teilen, jedoch erhält man dann keine ganze Zahl mehr. 91 kann man somit nicht mit der Zahl 3 kürzen.

Das Kürzen von Brüchen kann man auch als ein Verfeinern sehen. Denken wir an die Balkentafel, so kürzen wir, indem wir die blau einfärbte Fläche noch gröber unterteilen.
Man kürzt einen Bruch, indem man sowohl Zähler, als auch Nenner durch die selben Zahl dividiert.
Um von 42 zu 21 zu gelangen, muss man den Zähler (die 2) und den Nenner (die 4) durch 2 teilen.
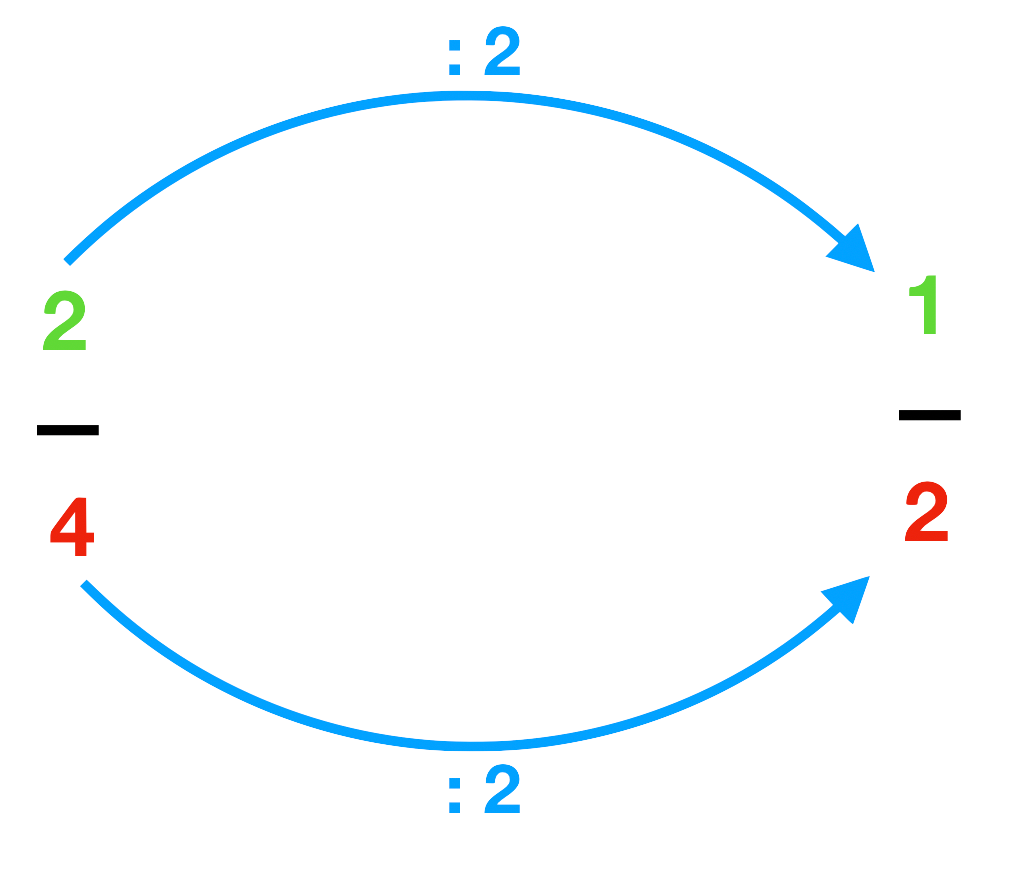
Brüche können nur ganze Zahlen enthalten. Beachte das insbesondere beim Vergröbern!

https://editor.mnweg.org/entdecken/dokument/4c15f5a1
Beispiele
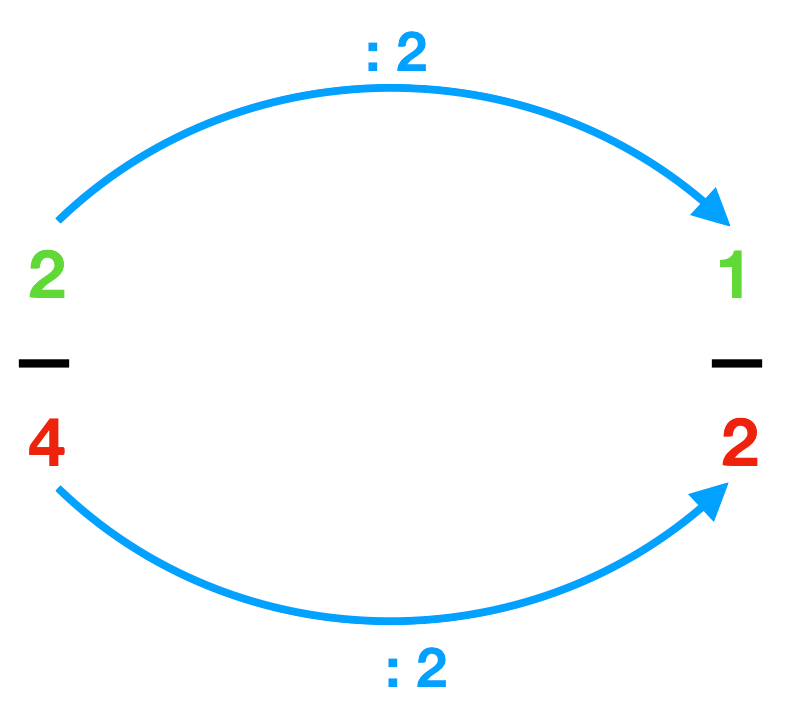
Aus 42 werden 21 , indem man Zähler (2) und Nenner (4) jeweils durch 2 dividiert.
Teilt man eine Pizza beispielsweise in 4 Teile und isst man 2 davon, so ist das das Gleiche, wie wenn man direkt die Pizza in 2 Teile geteilt und 1 davon gegessen hätte.
1.

2.
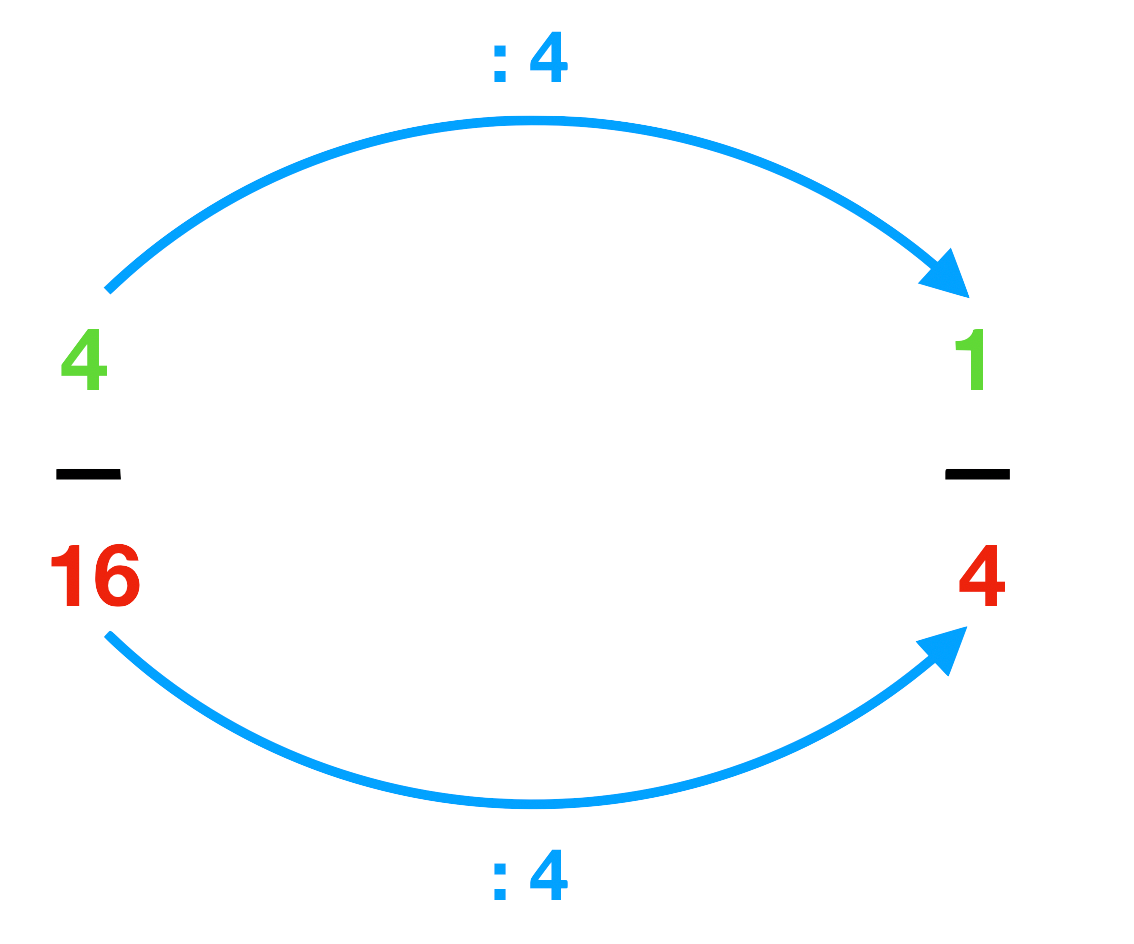
Aus 164 werden 41 , indem man Zähler (4) und Nenner (16) jeweils durch 4 teilt.

3.
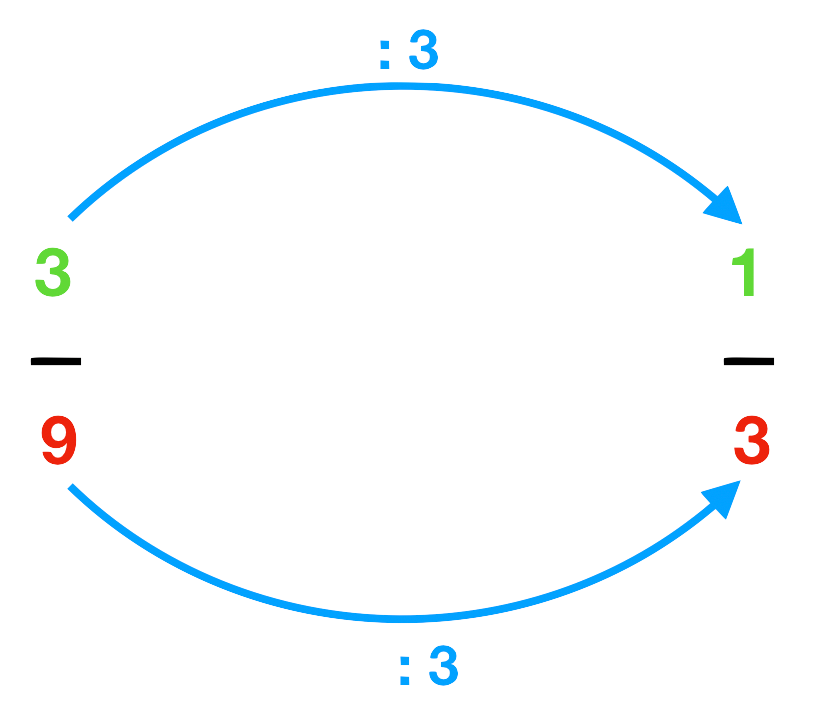
Aus 93 werden 31 , indem man Zähler (3) und Nenner (9) jeweils durch 3 teilt.

https://editor.mnweg.org/entdecken/dokument/4c15f5a1


