HerunterladenAls PDF Herunterladen
  • Teste dein Wissen
  • Winterhalter
  • 16.05.2019
  • Mathematik
  • Bruchrechnen
  • R
  • 5
  • Einzelarbeit
  • Arbeitsblatt
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
Teste dein Wissen
Mathematik Bruchrechnen R 5
1
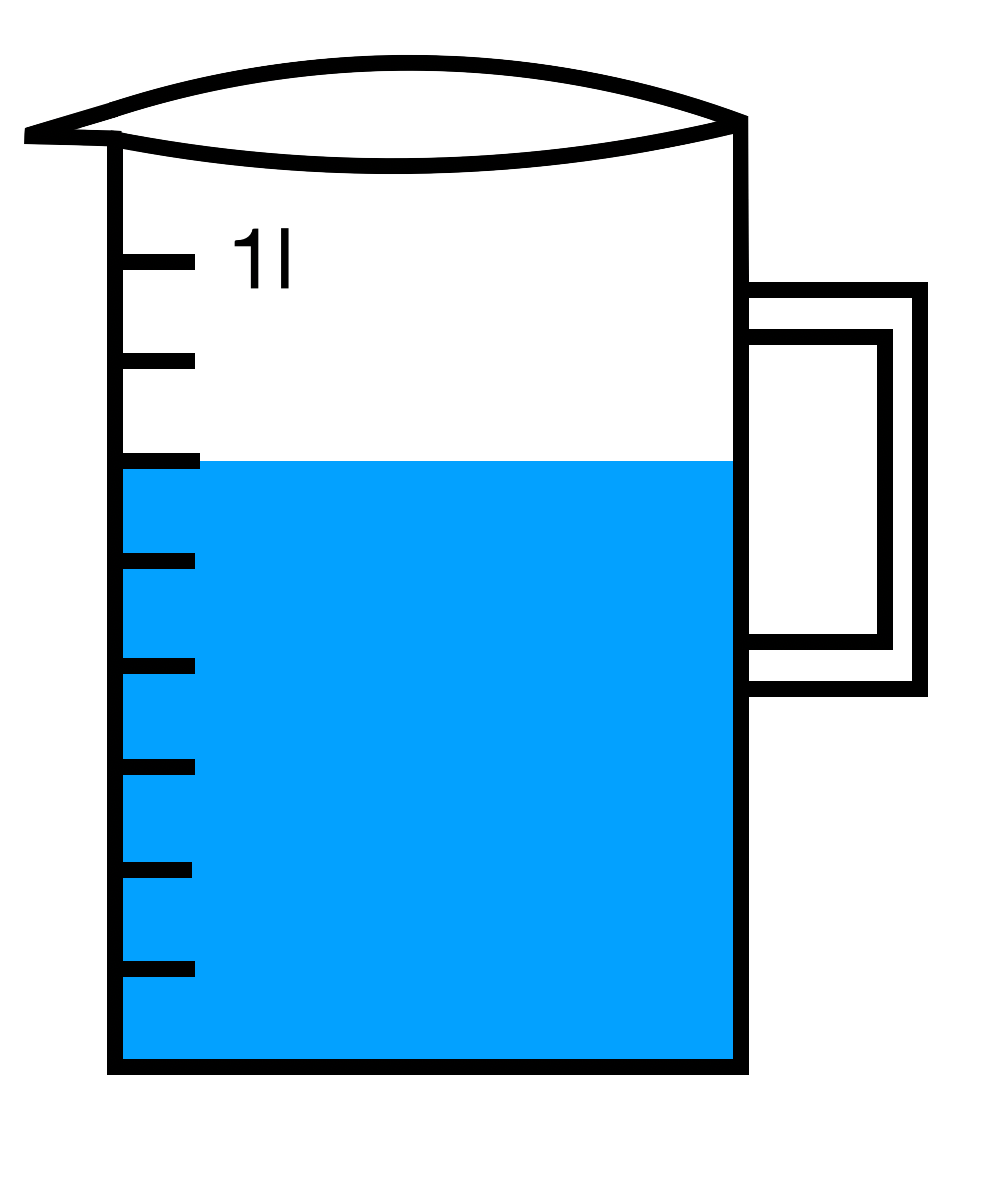
Welche Brüche sind hier dargestellt? Achte auf die angegebenen Einheiten.

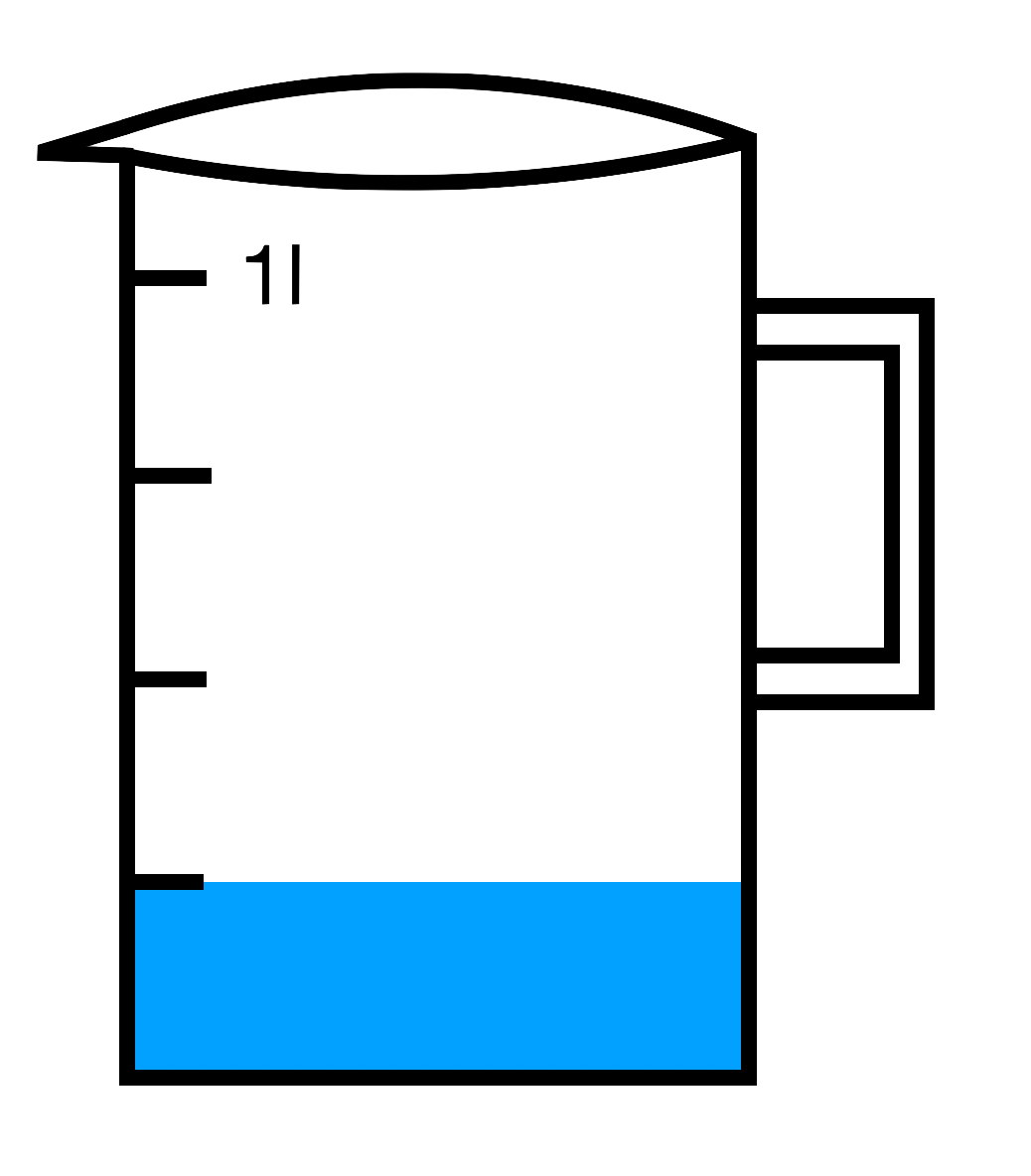
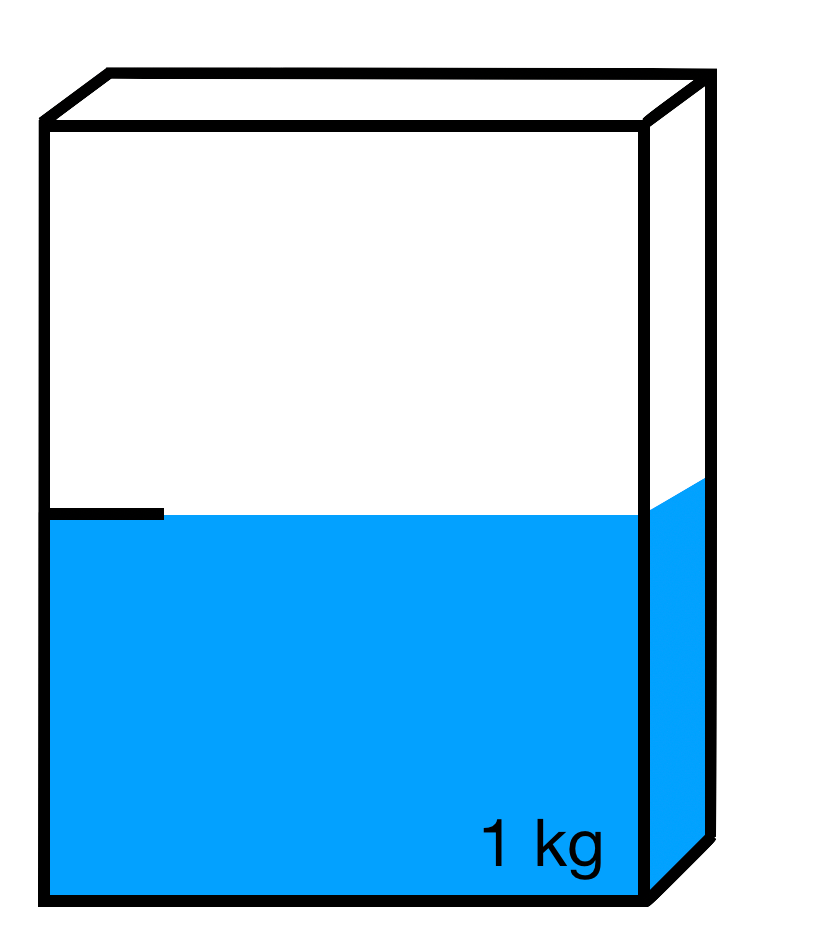
Vergangene Zeit seit 5 Uhr:

14\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \cloze{\frac{1}{4}} l

12\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \cloze{\frac{1}{2}} kg

14\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \cloze{\frac{1}{4}} h

34\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \cloze{\frac{3}{4}} m

68\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \cloze{\frac{6}{8}} l

2
Erweitere mit den angegebenen Zahlen.

  • \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} Erweitere 35\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \dfrac{3}{5} mit der Zahl 4


    \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} Erweitere 14\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \dfrac{1}{4} mit der Zahl 2



    (Auf der nächsten Seite hast du genügend Platz um die Lösung hinzuschreiben.)
3
Kürze mit den angegebenen Zahlen.

  • \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} Kürze 46\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \dfrac{4}{6} mit der Zahl 2


    \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} Kürze 915\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \dfrac{9}{15} mit der Zahl 3


a)

a)

b)

b)

Bereitgestellt von: Winterhalter Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/53799c05
Seite: 1/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/53799c05
AB
Teste dein Wissen
Mathematik Bruchrechnen R 5
Lösung2
Er­wei­te­re mit den an­ge­ge­be­nen Zah­len.

a) \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 1220\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \dfrac{12}{20} \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.36cm} b) \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 28\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \dfrac{2}{8}
Lösung3
Kürze mit den an­ge­ge­be­nen Zah­len.

a) \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 23\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \dfrac{2}{3} \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.36cm} b) \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 35\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \dfrac{3}{5}
4
Mit welchen Zahlen kannst du folgende Brüche kürzen? Trage deine Antwort in den grauen Bereich hinter dem jeweiligen Bruch ein.


  • \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 68\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \dfrac{6}{8} \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.6cm}


  • \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 69\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \dfrac{6}{9} \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.6cm}


  • \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 812\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \dfrac{8}{12} \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.4cm}


  • \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 1020\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \dfrac{10}{20} \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.4cm}
Bereitgestellt von: Winterhalter Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/53799c05
Seite: 2/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/53799c05
x