Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
Brüche richtig erkennen II
Mathematik Bruchrechnen M 5
1
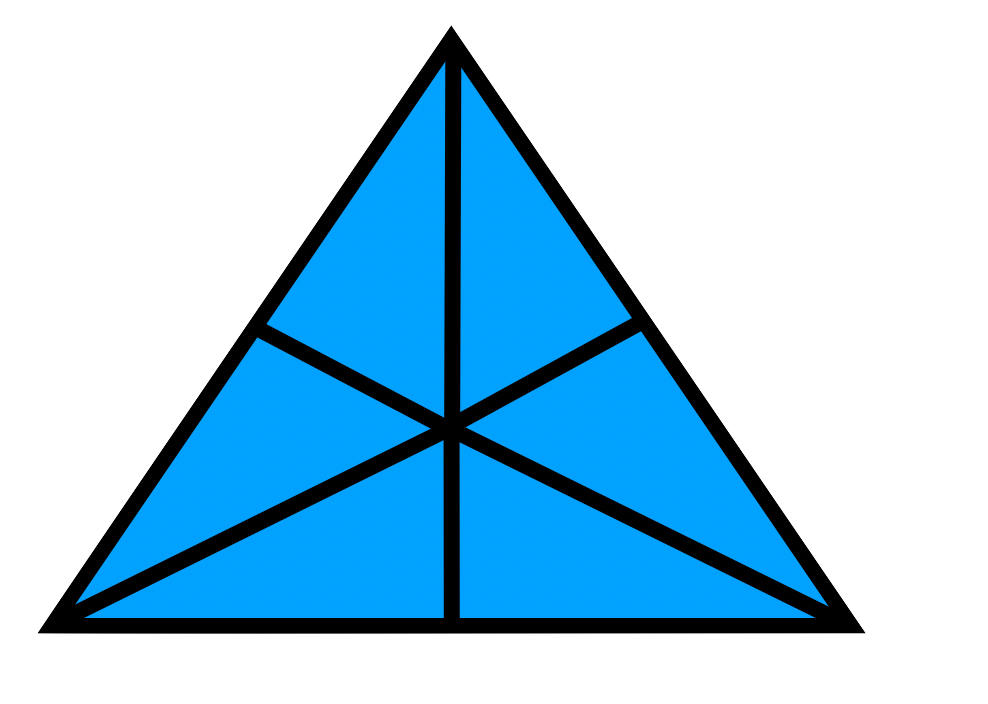
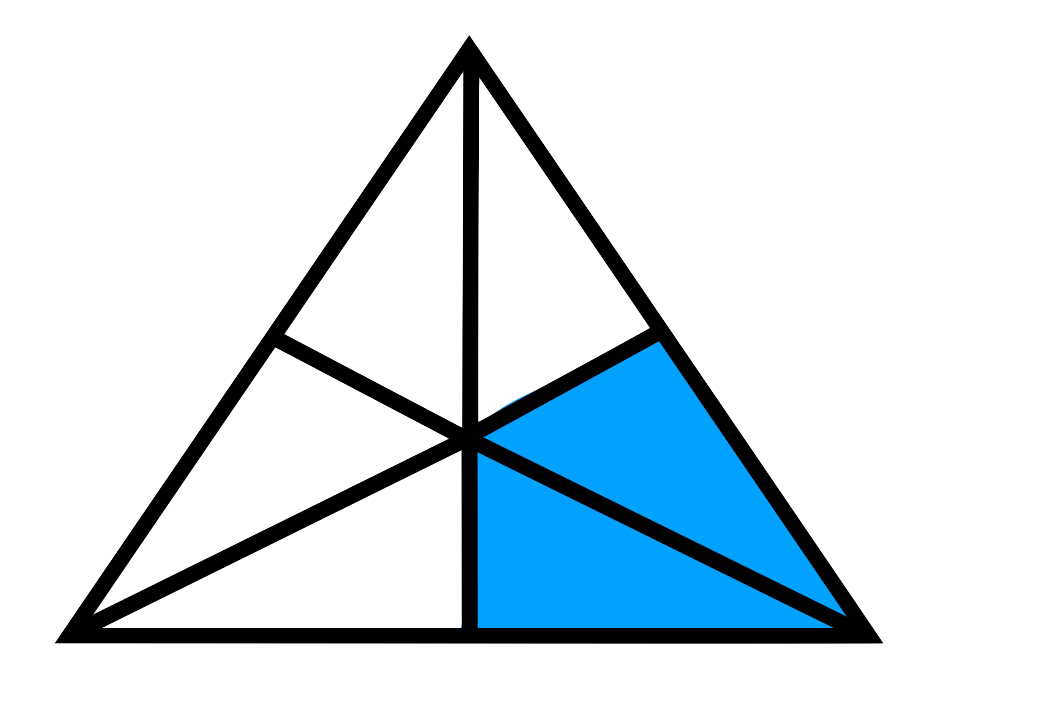
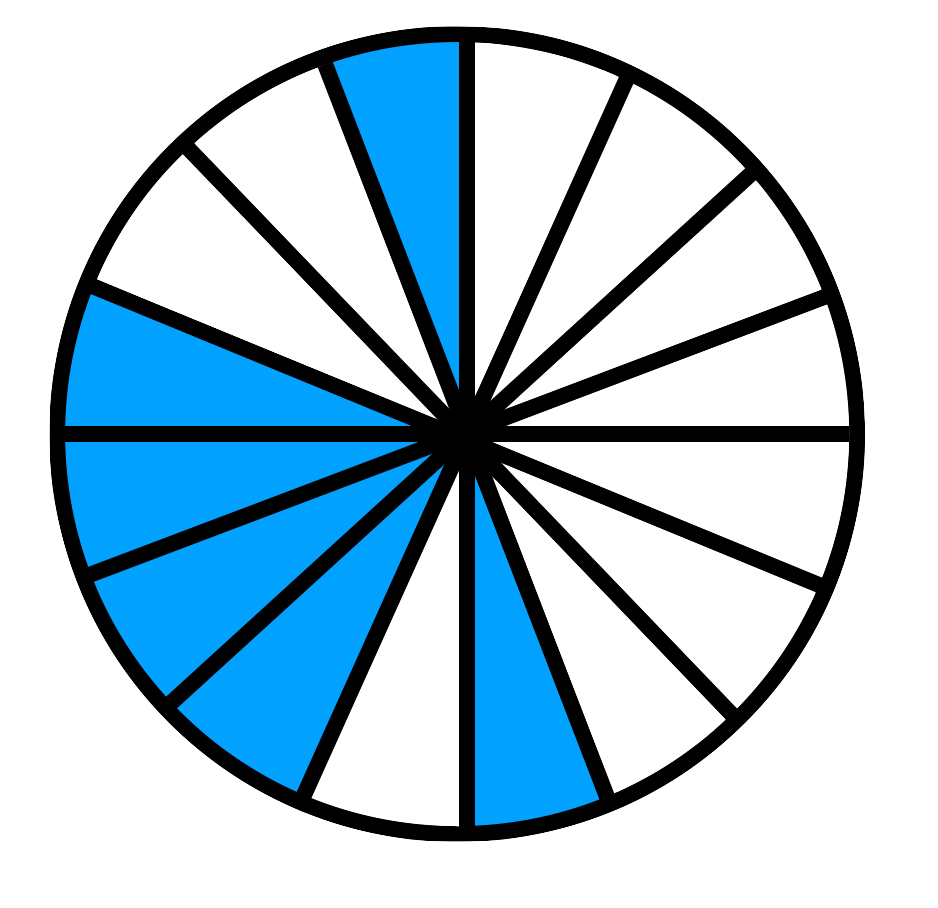
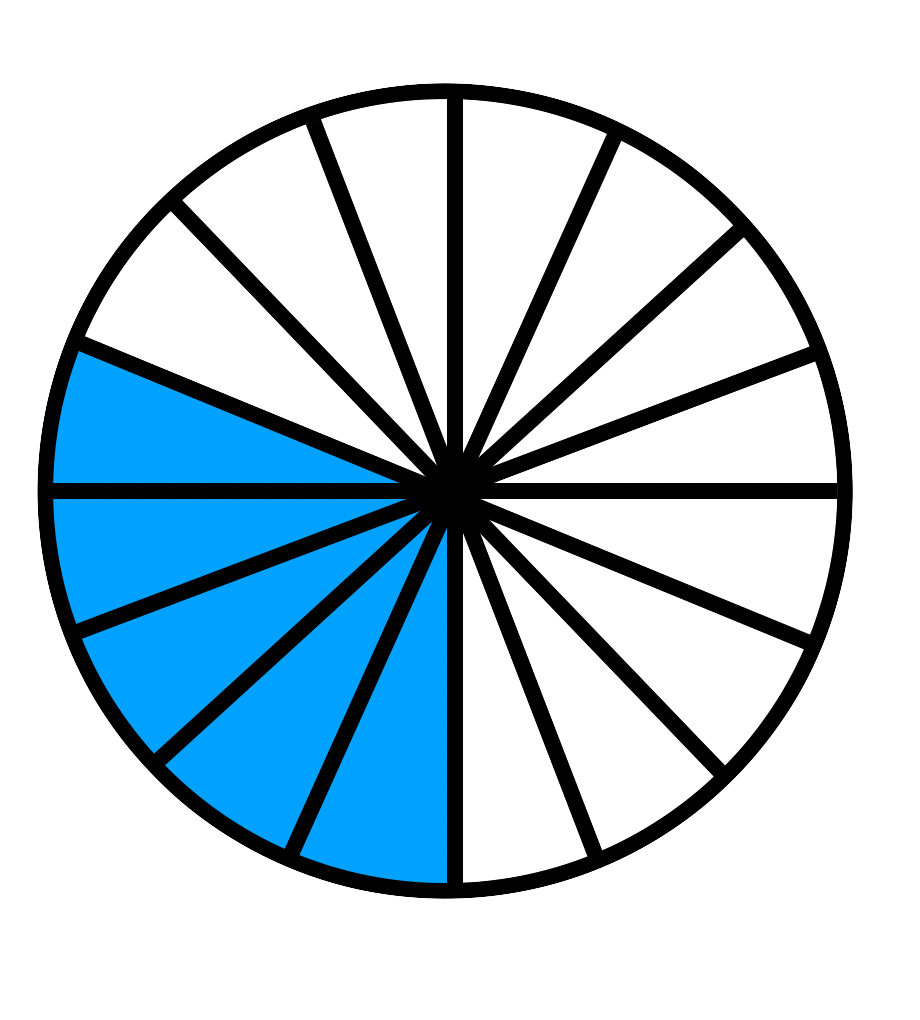
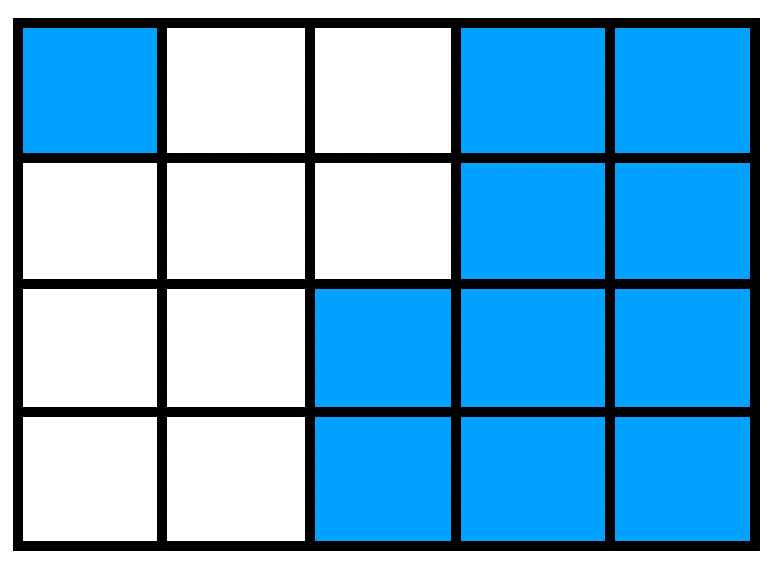
Welcher Bruch ist hier dargestellt? Schreibe den Bruch unter die jeweilige Grafik.



83
103
166


66
164
168

62
166
102

2011
2010
165
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/55a863e1
https://editor.mnweg.org/entdecken/dokument/55a863e1


