Name: Materialnetzwerk e. G.
Address: Endersstr. 33, Wutöschingen, BW, 79793
Telephone: +49 7746 92 85 70

TitelBrüche erweitern II
AutorStüer
veröffentlicht21.07.2020
FachMathematik
KompetenzbereichBruchrechnen
NiveaustufeR (Regelstandard)
Phase5
SozialformEinzelarbeit
MaterialformArbeitsblatt

Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

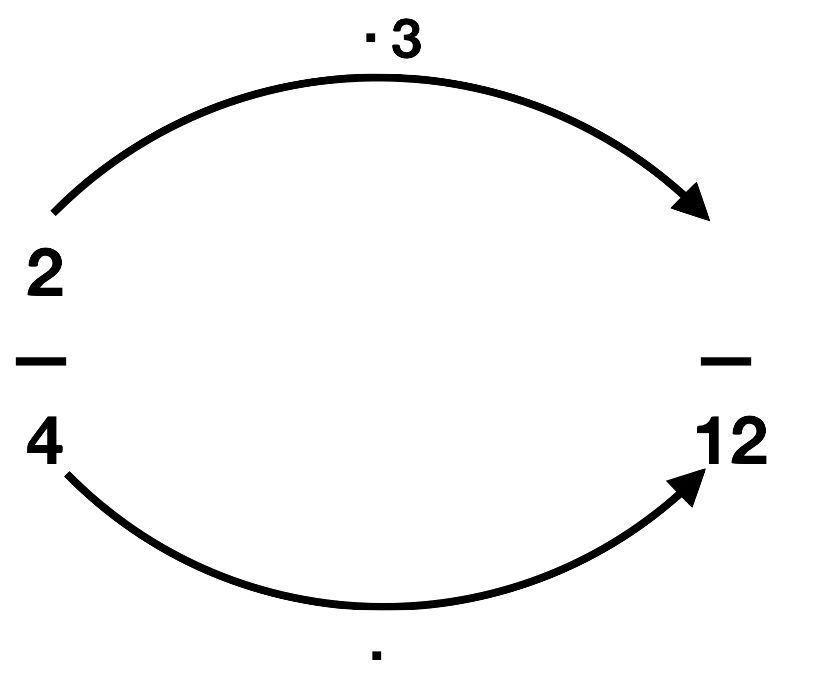
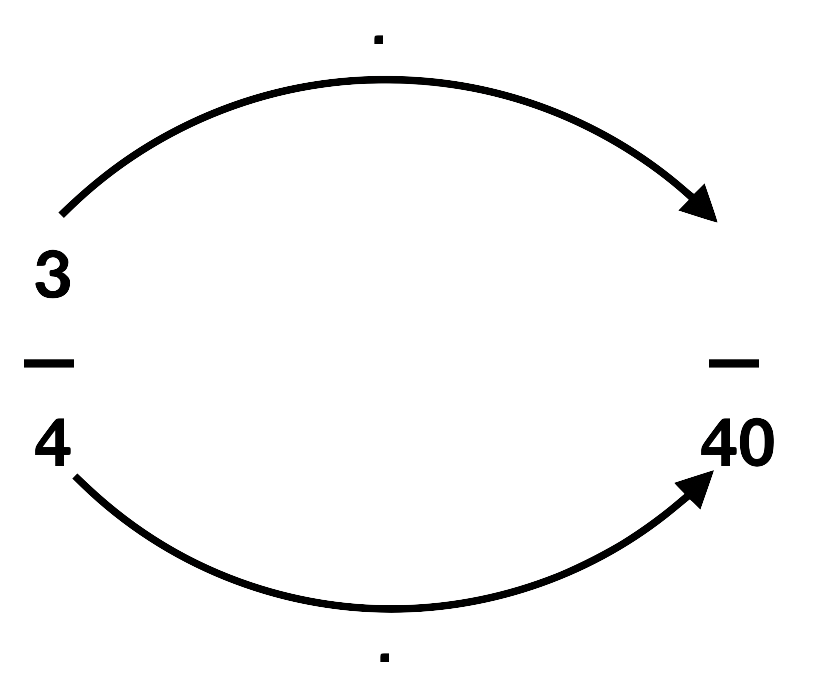
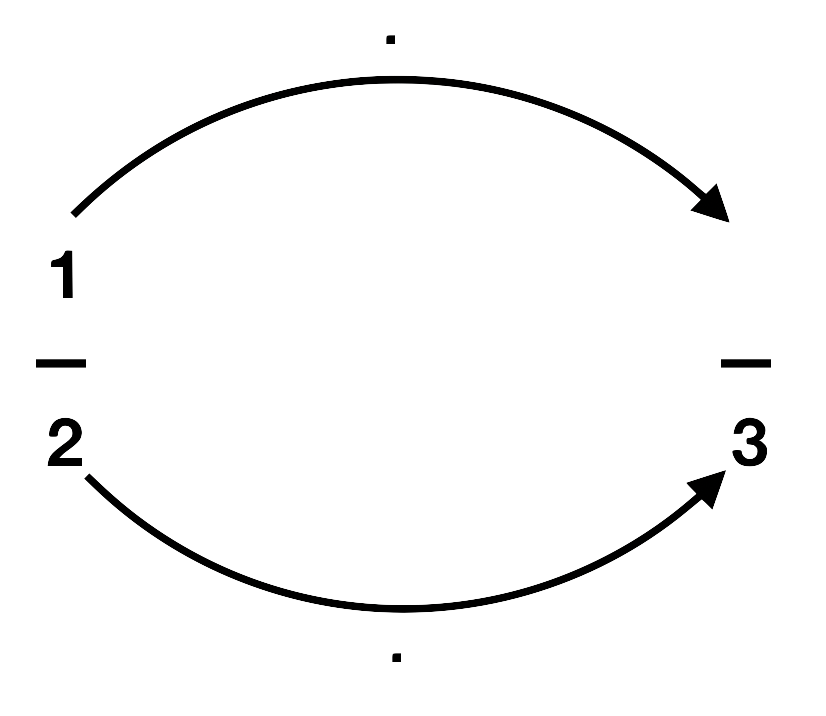
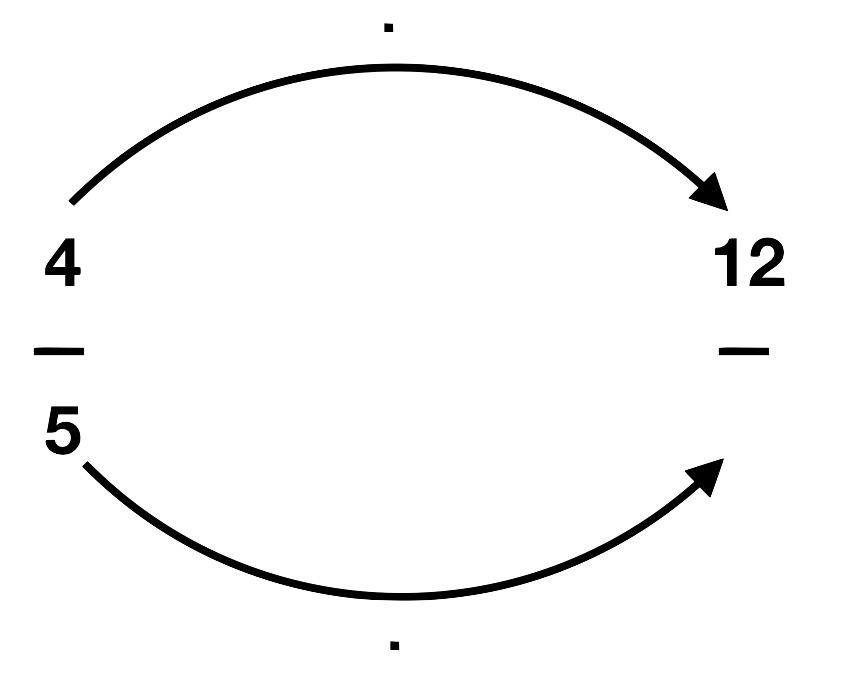
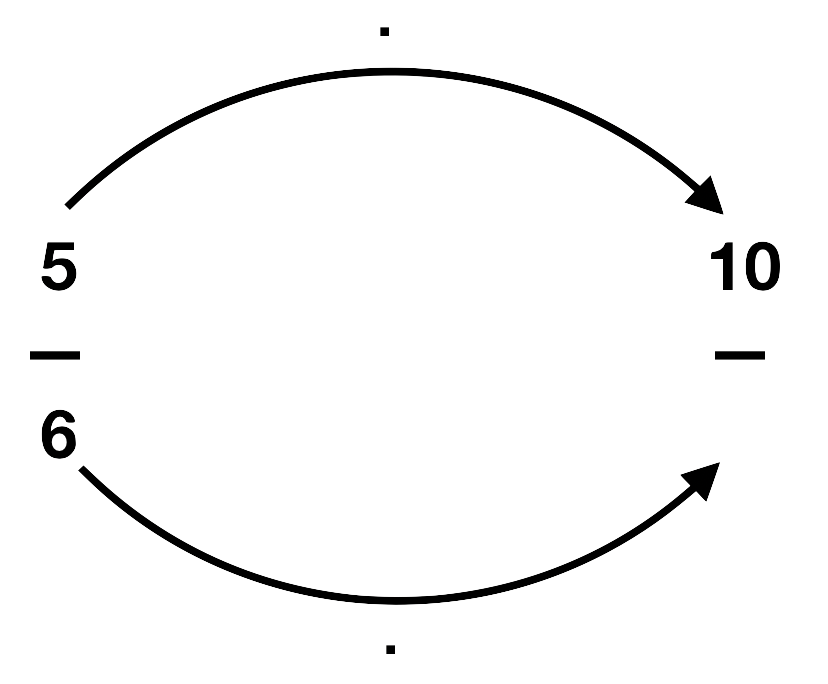
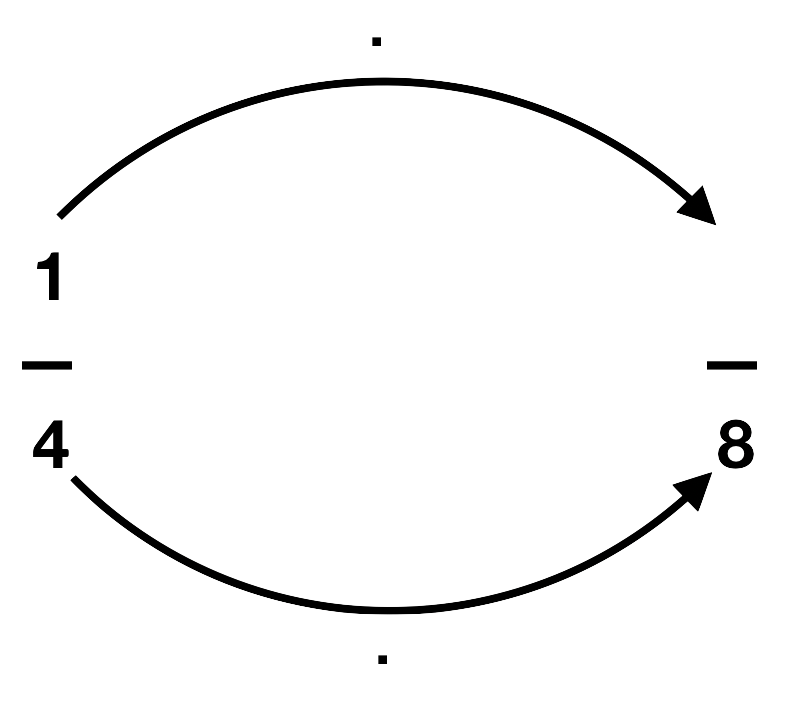
Welche Zahlen fehlen noch? Erweitere richtig und trage die fehlenden Zahlen in die Lücken ein. Aber aufgepasst: Bei einer Aufgabe hat sich ein Fehler eingeschlichen. Welcher Bruch lässt sich nicht erweitern?

Erweitere mit der angegebenen Zahl.

Erweitere den Bruch $\frac{1}{5}$ mit der Zahl $2$ : $\frac{1 \cdot 2}{5 \cdot 2}$ =
Erweitere den Bruch $\frac{3}{4}$ mit der Zahl $5$ : $\frac{3 \cdot 5}{4 \cdot 5}$ =
Erweitere den Bruch $\frac{1}{10}$ mit der Zahl $5$ : $\frac{1 \cdot 5}{10 \cdot 5}$ =
Erweitere den Bruch $\frac{14}{15}$ mit der Zahl $2$ : $\frac{14 \cdot 2}{15 \cdot 2}$ =
Erweitere den Bruch $\frac{2}{10}$ mit der Zahl $3$ : $\frac{2 \cdot 3}{10 \cdot 3}$ =
Erweitere den Bruch $\frac{1}{2}$ mit der Zahl $4$ : $\frac{1 \cdot 4}{2 \cdot 4}$ =
Erweitere den Bruch $\frac{1}{3}$ mit der Zahl $2$ : $\frac{1 \cdot 2}{3 \cdot 2}$ =
Erweitere den Bruch $\frac{2}{7}$ mit der Zahl $2$ : $\frac{2 \cdot 2}{7 \cdot 2}$ =
Erweitere den Bruch $\frac{1}{4}$ mit der Zahl $3$ : $\frac{1 \cdot 3}{4 \cdot 3}$ =
Erweitere den Bruch $\frac{1}{3}$ mit der Zahl $10$ : $\frac{1 \cdot 10}{3 \cdot 10}$ =
Erweitere den Bruch $\frac{2}{4}$ mit der Zahl $5$ : $\frac{2 \cdot 5}{4 \cdot 5}$ =