HerunterladenAls PDF Herunterladen
  • Brüche erkennen
  • Deliah Herbstritt
  • 21.07.2020
  • Mathematik
  • Bruchrechnen
  • M (Mindeststandard)
  • 5
  • Einzelarbeit
  • Folie
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
Folie
Brüche erkennen
Mathematik Bruchrechnen M 5
1
Gib den gefärbten Anteil als Bruch an.
Du brauchst eine Vorbereitung für den GN?

Versuche es doch mal mit den QR-Codes!

https://www.matheretter.de/test/bruch/1
https://www.matheretter.de/test/bruch/3
Bereitgestellt von: Deliah Herbstritt Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/7d86118c
Seite: 1/3
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/7d86118c
Folie
Brüche erkennen
Mathematik Bruchrechnen M 5
2
Färbe jeweils den angegebenen Bruchteil der Fläche in deiner Lieblingsfarbe.
3
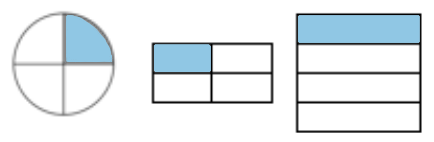
Welcher Bruchteil ist hier dargestellt? Was fällt dir auf? Haben die Brüche Gemeinsamkeiten?
Bereitgestellt von: Deliah Herbstritt Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/7d86118c
Seite: 2/3
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/7d86118c
Folie
Brüche erkennen
Mathematik Bruchrechnen M 5
4
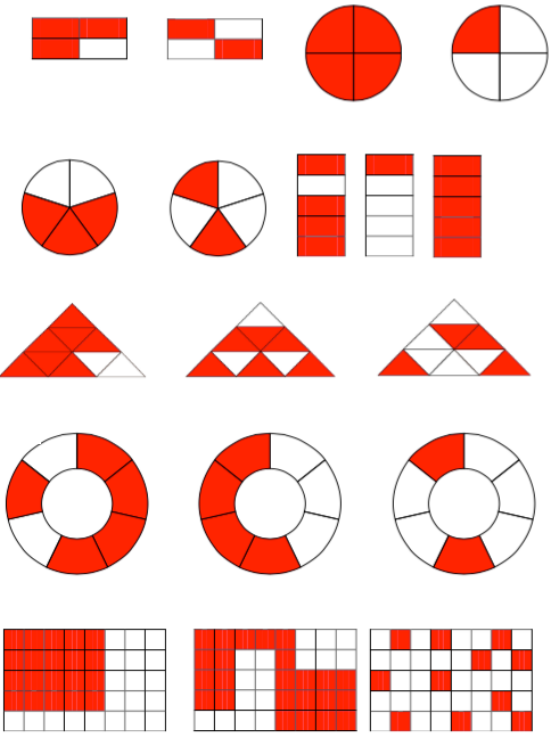
Welche Brüche sind dargestellt?
Bereitgestellt von: Deliah Herbstritt Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/7d86118c
Seite: 3/3
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/7d86118c
x