Anzahl und Anteile II

AB
Anzahl und Anteile II
Mathematik Bruchrechnen M 5
1
Elfmeterschießen:
Nach der Schule treffen sich ein paar Freunde und wollen Fußball spielen. Sie wollen ein wenig ihre Elfmeterschüsse verbessern. Dafür teilen sie sich in zwei 6er-Teams auf. Beim Elfmeterschießen hat jeder genau einen Versuch frei. Kims Team trifft 4 Mal und Alexanders Team trifft 3 Mal.

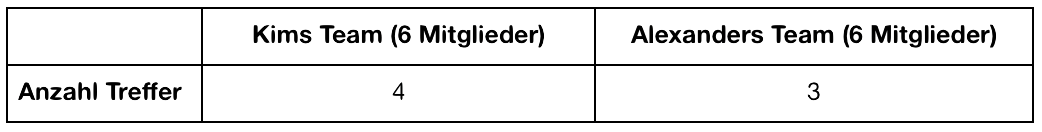
Welches Team hat gewonnen? Warum reicht es hier, nur die Anzahl der Treffer miteinander zu vergleichen? Wieso ist es nicht zwingend nötig, die Balkentafel bzw. Anteile an Treffern zu vergleichen?

Bereitgestellt von: Winterhalter Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/864167d4
Seite: 1/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/864167d4
AB
Anzahl und Anteile II
Mathematik Bruchrechnen M 5
Bereitgestellt von: Winterhalter Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/864167d4
Seite: 2/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/864167d4

Anzahl und Anteile II

von Winterhalter
Mathematik
Bruchrechnen
M (Mindeststandard)
5
Einzelarbeit
Arbeitsblatt
21.07.2020
Mehr entdecken:

Lizenzhinweis

Alle Bestandteile dieses Materials sind frei oder unlizenziert. Klicken Sie auf einen Baustein, um die Lizenz zu sehen.
x