Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
Anwendungsaufgaben Pythagoras
Mathematik Flächen R 9
1
Azubi Peter soll im Auftrag seiner Firma Bleistifte als Werbegeschenke verschicken. Diese sollen in Boxen mit der Länge 12 cm, der Breite 9 cm und der Höhe 4 cm verpackt werden.
Welche Länge dürfen die Bleistifte höchstens haben?
Welche Länge dürfen die Bleistifte höchstens haben?

2
Herr Würth hat einen Steinquader mit der Länge 5 m, der Breite 0,5 m und der Höhe 0,7 m in seinem Garten.
Da er gerade mit seiner Enkelin den Satz des Pythagoras geübt hat, beginnt er die Grundflächendiagonale und die Raumdiagonale des Steinquaders zu berechnen.
Kannst du das auch?
Berechne die Diagonalen und fertige gegebenenfalls eine Skizze an.
Da er gerade mit seiner Enkelin den Satz des Pythagoras geübt hat, beginnt er die Grundflächendiagonale und die Raumdiagonale des Steinquaders zu berechnen.
Kannst du das auch?
Berechne die Diagonalen und fertige gegebenenfalls eine Skizze an.

Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/a28697b8
https://editor.mnweg.org/entdecken/dokument/a28697b8
AB
Anwendungsaufgaben Pythagoras
Mathematik Flächen R 9
3
Das Dach einer Kirche hat die Form einer quadratischen Pyramide mit einer Seitenlänge von 9 m und einer Höhe von 7 m. Es soll neu eingedeckt werden.
Berechne die gesamte Dachfläche. Die Abbildungen können dir helfen!
Berechne die gesamte Dachfläche. Die Abbildungen können dir helfen!
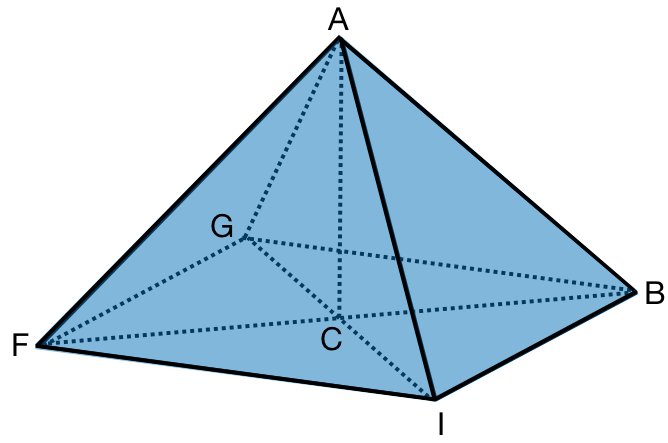
Pyramide (Dach der Kirche)
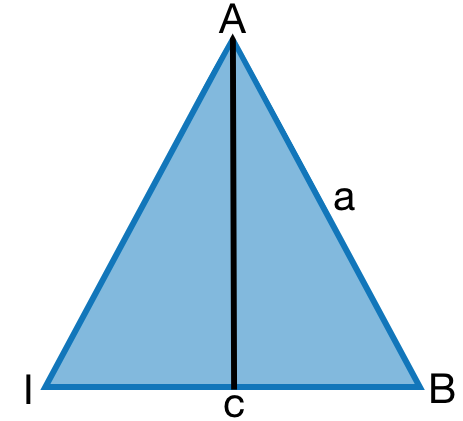
Hälfte der Pyramide
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/a28697b8
https://editor.mnweg.org/entdecken/dokument/a28697b8


