TitelSatz des Pythagoras
Autoranonym
veröffentlicht03.02.2020
FachMathematik
KompetenzbereichFlächen
NiveaustufeM (Mindeststandard)
Phase9
SozialformEinzelarbeit
MaterialformInformation

Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

Mit dem Satz des Pythagoras kannst du die Länge einer Seite von einem rechtwinkligen Dreieck berechnen. Hierfür sind zwei Seitenlängen des rechtwinkligen Dreiecks gegeben. Die Formel hierfür lautet:

$a^{2} + b^{2} = c^{2}$

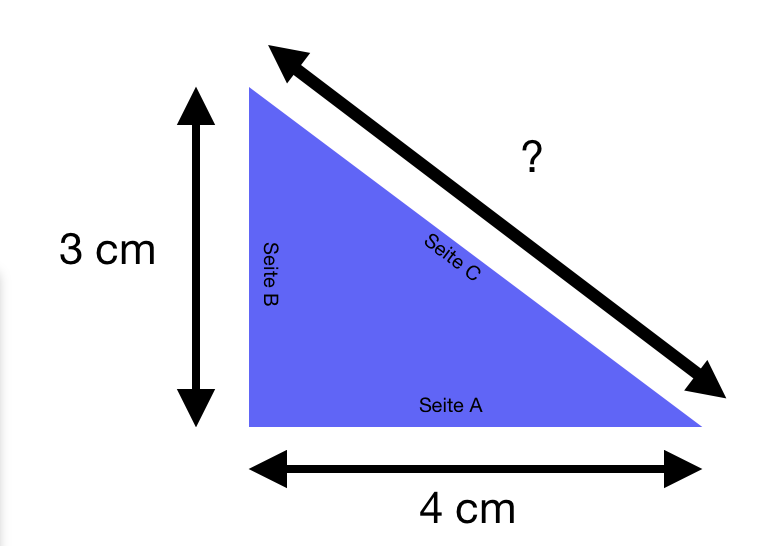
In dieser Grafik siehst du ein rechtwinkliges Dreieck, bei dem die Längen der beiden Katheten bekannt sind. Nun kann man mit dieser Formel die Hypotenuse ausrechnen:

$3^{2} + 4^{2} = 25$

$25 = \underline{\underline{5}}$

Antwort: Die Hypotenuse des rechtwinkligen Dreiecks ist 5 cm lang.

Die genauere Erklärung und Herleitung des Satz des Pythagoras findest du in diesem Video:

Achtung!

Nicht in jedem rechtwinkligen Dreieck ist die Seite c immer auch die Hypotenuse. Eigentlich heißt der Satz des Pythagoras:

Im rechtwinkligen Dreieck ist die Summe der Kathetenquadrate gleich dem Quadrat der Hypotenuse.