Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
Größer oder kleiner? III
Mathematik Bruchrechnen M 5
1
Schreibe unter jede Grafik den richtigen Bruch und füge
<oder
>zwischen die zwei Grafiken ein.

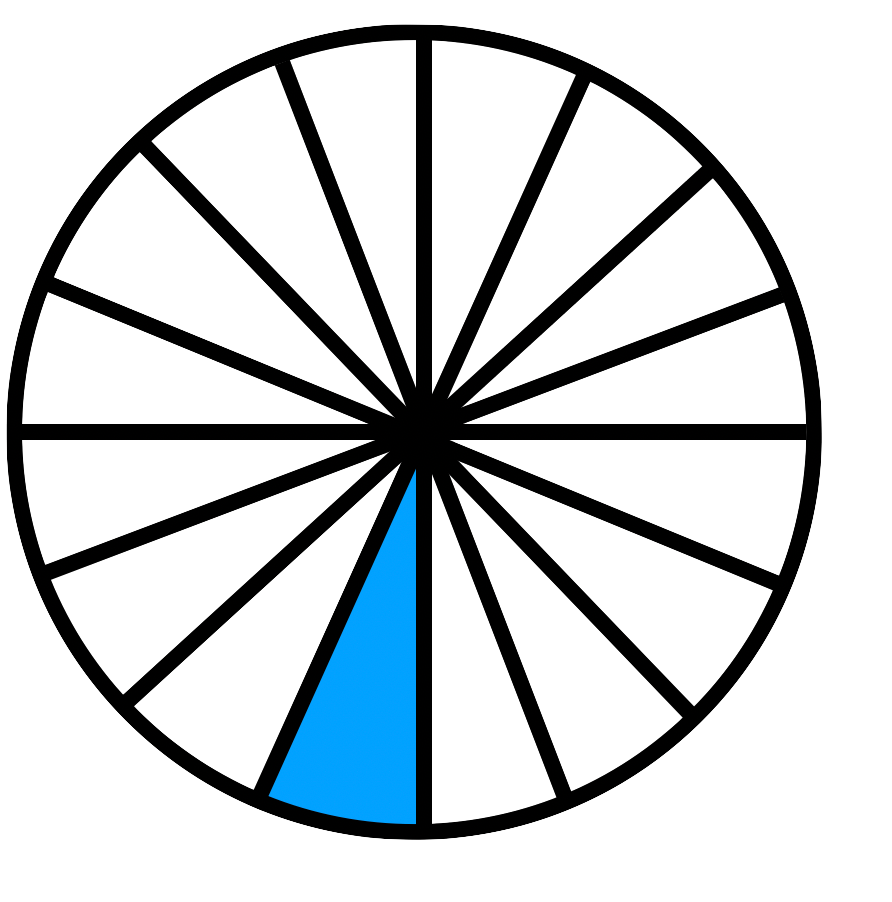

41
161



168
88



21
41
2
Vergleiche die zwei Brüche miteinander. Welcher Bruch ist größer? Setze die Zeichen
<und
>richtig in die grau gefärbten Lücken ein.
a) 42 43
d) 91 101
g) 32 31
b) 201 191
e) 211 221
h) 168 167
c) 2007 2003
f) 9001 9011
i) 3001 2001
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/ab6d9914
https://editor.mnweg.org/entdecken/dokument/ab6d9914


