Name: Materialnetzwerk e. G.
Address: Endersstr. 33, Wutöschingen, BW, 79793
Telephone: +49 7746 92 85 70

HerunterladenAls PDF Herunterladen

TitelBalkentafel Kürzen II
AutorWinterhalter
veröffentlicht16.05.2019
FachMathematik
KompetenzbereichBruchrechnen
NiveaustufeR (Regelstandard)
Phase5
SozialformEinzelarbeit
MaterialformArbeitsblatt

Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

Löse die Aufgabe Schritt für Schritt:

Welcher Bruch ist in der Balkentafel eingezeichnet?

$\frac{3}{9}$
Mit welcher Zahl kannst du diesen Bruch vergröbern?
(siehe Tipp)
Male den vergröberten Bruch in der Balkentafel an.
Welchen Bruch erhältst du nach dem Vergröbern?

$\frac{3 : 3}{9 : 3}$ = $\frac{1}{3}$

Tipp

Um herauszufinden, welchen Bruch man mit welcher Zahl vergröbern/verfeinern kann, kannst du dein Lineal verwenden. Fahre dafür mit dem Lineal senkrecht über die Balkentafel.

Löse die Aufgabe Schritt für Schritt:

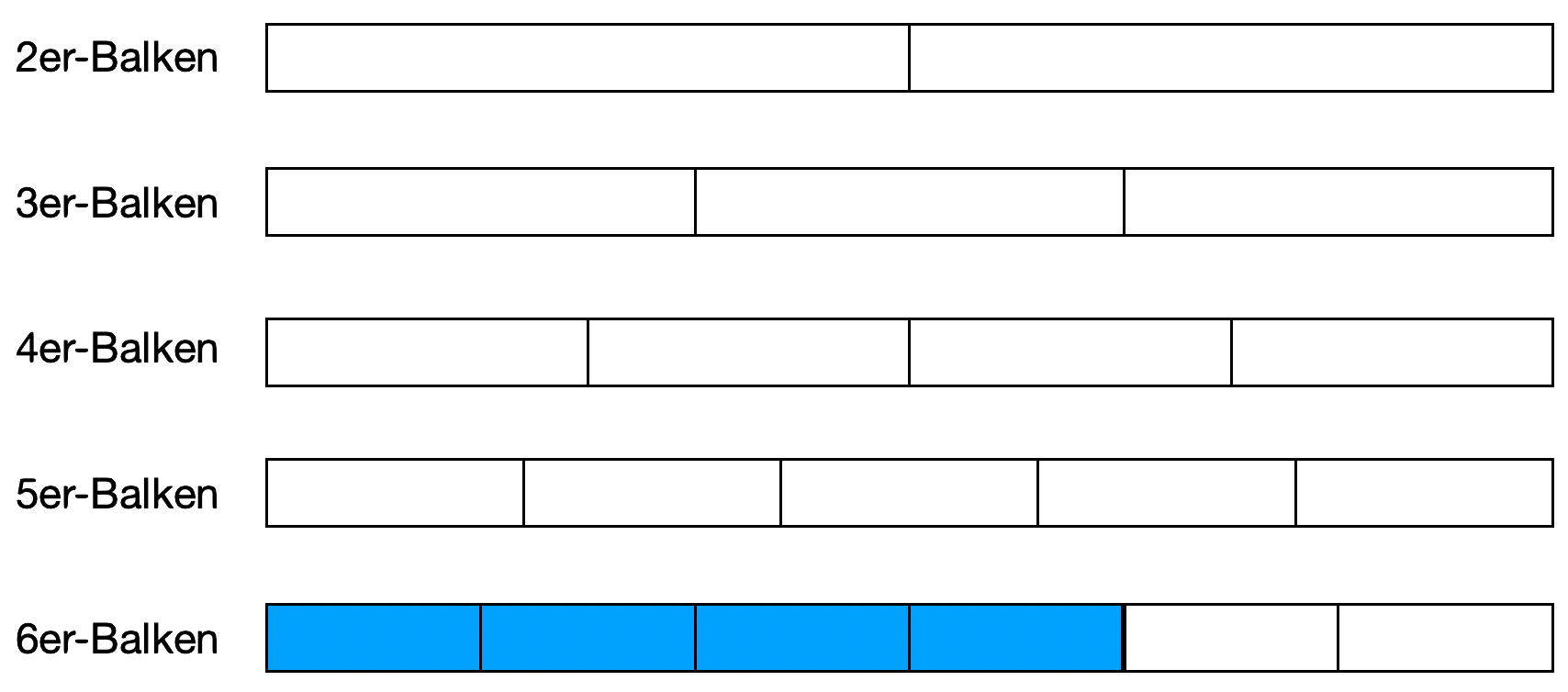
Welcher Bruch ist in der Balkentafel eingezeichnet?

$\frac{4}{6}$
Mit welche Zahl kannst du diesen Bruch vergröbern?
(siehe Tipp)
Male den vergröberten Bruch in der Balkentafel an.
Welchen Bruch erhältst du nach dem Vergröbern?

$\frac{4 : 2}{6 : 2} = \frac{2}{3}$