Nach diesem Baustein...
...kennst du die Begriffe Terme und Variablen
...beherrschst du es Terme zusammenzufassen
...weißt du, wie man Termwerte berechnet
...kannst du mathematische Beschreibungen und
Sachverhalte in Terme übersetzen und umgekehrt
Benötigtes Material:
Arbeitsblatt zum Baustein
Termbaukasten mit Trinkhalmen (licofun)
Zollstock/Meterstab
einen Würfel mit den Zahlen 1-6
Material "Termbingo"
Material "Termdomino"
Zeit: ca.180 Minuten
Zeit: ca.30 Minuten
Zeit: ca.10 bis 20 Minuten
Zeit: ca.90 Minuten
Zeit: ca.45 bis 60 Minuten
Dieses Symbol zeigt dir, dass die nachfolgende Aufgabe eine besonders herausfordernde Aufgabe ist. Du kannst diese freiwillig bearbeiten.
Manche Aufgaben findest du auf dem zugehörigen Arbeitsblatt, damit du nicht so viel abschreiben musst.
Bevor du diesen Baustein beginnst, solltest du den Baustein Umfang und Flächeninhalt bereits bearbeitet haben.
Prüfe, ob du bereit für diesen Baustein bist, indem du
das folgende Online-Quiz löst.
Scanne den QR-Code, um zum Quiz zu gelangen.
Falls du Probleme beim Lösen der Aufgaben hast,
sprich deine Lernbegleitung an.
Link:
https://learningapps.org/watch?v=p0gaucvzt22
https://learningapps.org/
watch?v=p0gaucvzt22
https://editor.mnweg.org/entdecken/dokument/baustein-terme
Einführung - Vom Trinkhalm zum Term
Bevor wir genau klären, was Terme sind, werden wir uns im folgenden Abschnitt dem Begriff Term annähern. Vieles wird dir bekannt vorkommen.
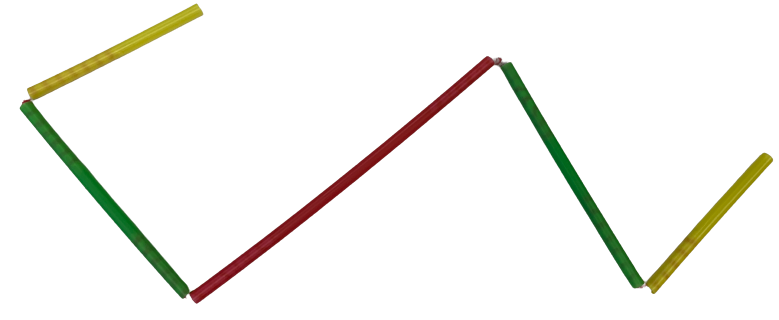
Tim hat die Trinkhalme zu einem sogenannten Streckenzug zusammengesteckt.
Für die Länge des Streckenzuges notiert Tim
gelb+gru¨n+rot+gru¨n+gelb
Jetzt bist du dran!
Hinweis: Dein Streckzug muss mindestens 6 Trinkhalme lang sein.
Tims Geodreieck ist zu klein, um seinen kompletten Streckenzug zu messen. Deswegen addiert Tim die Längen der einzelnen Trinkhalme. Also für gelb 7,5cm für grün 10cm usw.
Somit kommt er auf 7,5cm+10cm+15cm+10cm+7,5cm=50cm
Wie lang ist dein Streckenzug?
Hinweis: Um deine Rechnung zu überprüfen, kannst du mit einem Zollstock deinen kompletten Streckenzug nachmessen.
- Notiere die Länge von deinem neuen Streckenzug.
- Wieso verändert sich die Länge des Streckenzuges nicht?
https://editor.mnweg.org/entdecken/dokument/baustein-terme
Mathematisch schreiben und zusammenfassen
Tim dauert es zu lang, wenn er gelb + gelb + grün usw. ausschreiben muss...
Seine Lernbegleitung kann ihm weiterhelfen und verrät ihm, dass es den Mathematikern und Mathematikerinnen auch so geht und wir aus diesem Grund in der Mathematik die Begriffe durch Kleinbuchstaben (Variablen) ersetzen.
Deshalb wählt Tim für die Farbe blau den Buchstaben b, für gelb , für grün y, für rot x und für schwarz a.
Wir werden Tims Wahl übernehmen und in den weiteren Rechnungen
die Variablen a, b, , x und y verwenden.
Statt + gru¨n + rot + gru¨n + schreiben wir: + y + x + y + .






Einen Platzhalter für Zahlen aus einer Grundmenge nennt man in der Mathematik auch Variable und verwendet dafür Kleinbuchstaben.
- Bsp.:
Die Länge für Tims Streckenzug lässt sich zusammenfassen, da man statt
c+c+x+y+y auch 2⋅c+x+2⋅y schreiben kann.
https://editor.mnweg.org/entdecken/dokument/baustein-terme
Streckenzüge zusammenfassen
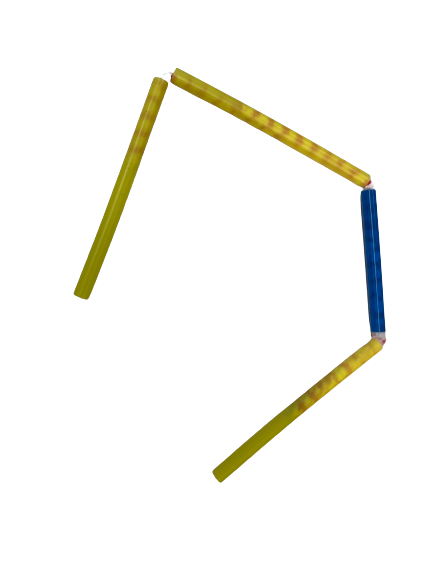
c+c+b+c ist die Länge des Streckenzuges

Bsp.
a+b+b+a+x
=2⋅a+2⋅b+x

- Bsp.: 25cm=rot+blau+blau=x+b+b=x+2⋅b
b) 50cm
c) 67,5cm
d) 47,5cm
Schreibe die Lösungen in dein Heft.
https://editor.mnweg.org/entdecken/dokument/baustein-terme
Der Umfang und das Distributivgesetz
Mit den Trinkhalmen lassen sich nicht nur Streckenzüge legen, sondern auch geometrische Figuren, wie z.B. Rechtecke und Quadrate.

- Gib den Umfang mit den Variablen a (schwarz) und c (gelb) an.
Schreibe die Lösung in dein Heft.
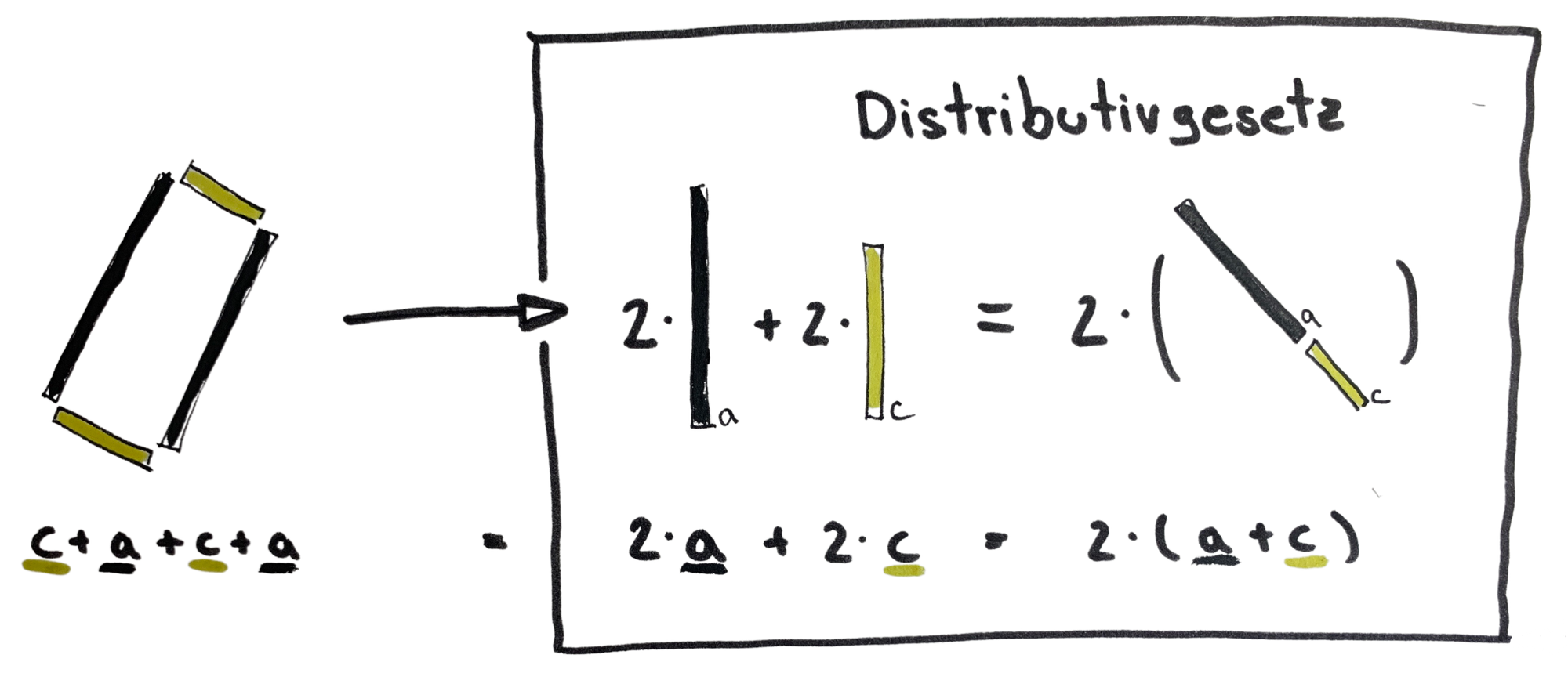
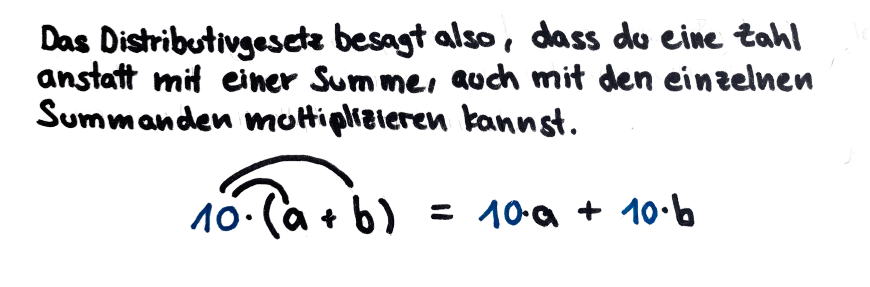
Bsp. 1 2⋅(a+b)=2⋅a+2⋅b
Bsp. 2 3⋅x+3⋅d=3⋅(x+d)
- 3⋅q+3⋅u
- 4⋅(y+d)
- 2⋅(f+g)
- 6⋅x+6⋅y
https://editor.mnweg.org/entdecken/dokument/baustein-terme

- Gib den Umfang und den Flächeninhalt möglichst kurz mit Variablen an.
Schreibe die Lösungen in dein Heft.
- Zeichne zwei verschiedene Möglichkeiten in dein Heft.
- Gib den dazugehörigen Umfang mit Variablen an.
Schreibe die Lösung in dein Heft.
- Gib den Flächeninhalt mit Variablen an.
Schreibe die Lösung in dein Heft.
Findest du verschiedene Möglichkeiten den Flächeninhalt zu halbieren?
Was ist ein Term?
Jedes Mal, wenn du die Länge eines Streckenzuges, den Umfang eines Rechtecks oder seinen Flächeninhalt angibst, schreibst du einen Term. Seit der 1. Klasse schreibst du Terme im Mathematikunterricht auf.
Ein Term ist ein mathematischer Ausdruck, der aus einer sinnvollen Zusammenstellung von Zahlen und / oder Variablen mit Rechenzeichen und / oder Klammern besteht.
Du hast dich jetzt intensiv mit Termen, in Form von Streckenzügen, auseinandergesetzt.
Löse das Check-Out zu diesem Abschnitt auf dem Arbeitsblatt, um die Einführung in die Terme abzuschließen.
https://editor.mnweg.org/entdecken/dokument/baustein-terme
Termbingo - In Terme einsetzen
Suche dir bis zu 3 weitere Mitspieler oder Mitspielerinnen. Du kannst das Spiel aber auch alleine spielen. Spielt höchstens 30 Minuten.
- eines der beiden Termbingos (das blaue Bingo ist eine Herausforderung, wählt dieses, falls ihr euch im Umgang mit Termen schon sicher fühlt), zu jedem Bingo gehören 4 Zahlenfelder und 6 Termkarten
- einen Würfel mit den Zahlen 1-6 und etwas zum Abdecken der Zahlen in den 3x3-Zahlenfeldern, zum Beispiel Chips, Münzen oder Papierschnipsel (im Folgenden als
Abdeckchips
bezeichnet)
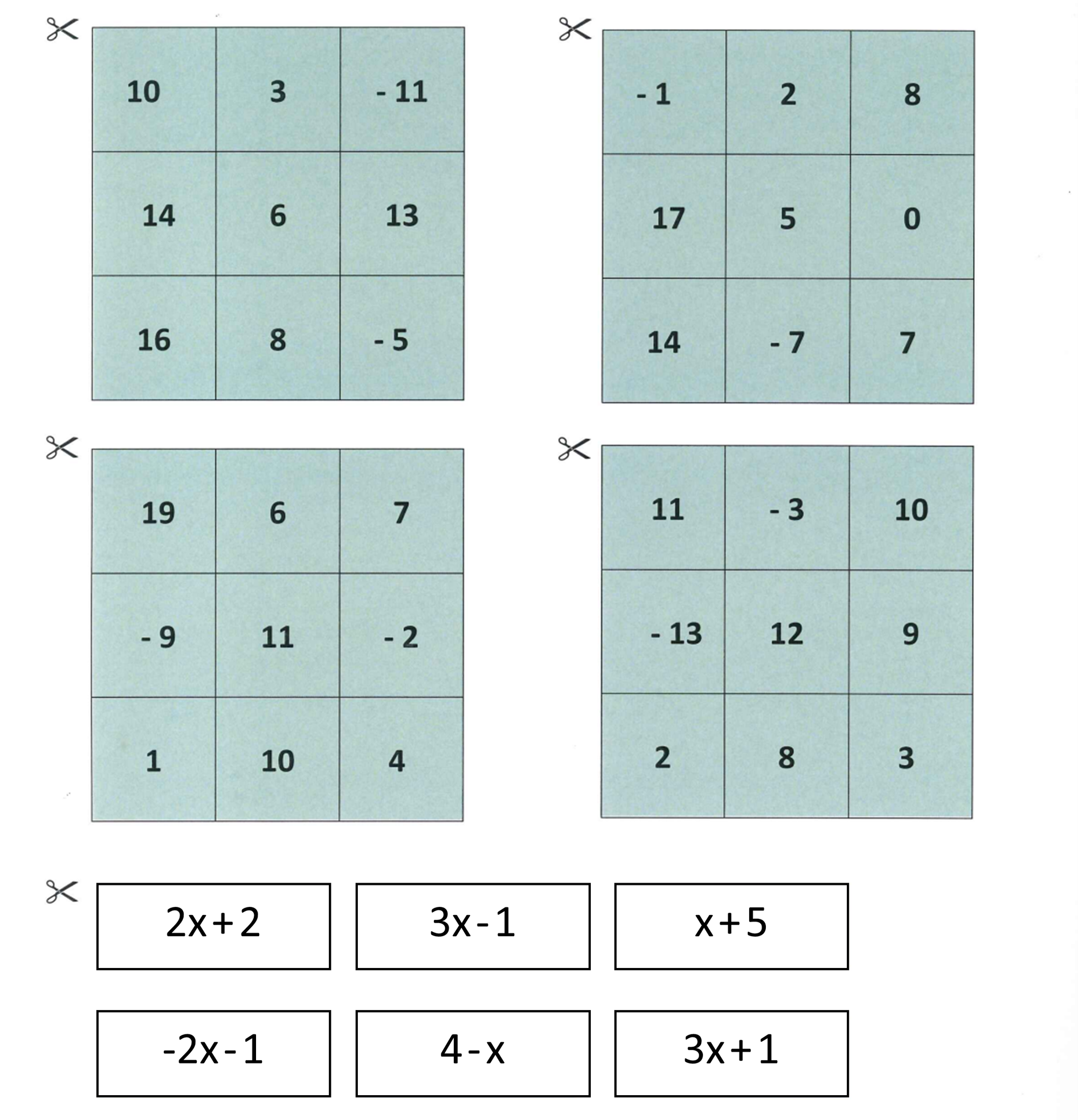
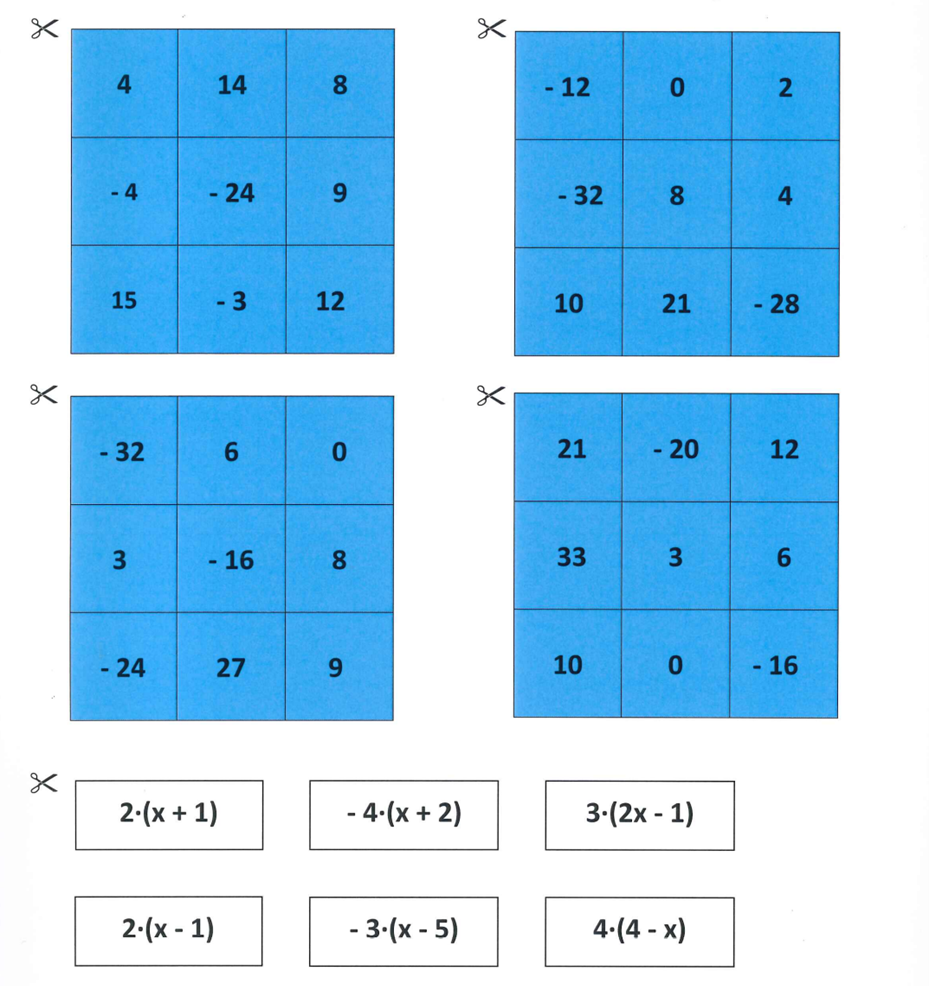


Alle Mitspieler und Mitspielerinnen erhalten jeweils ein 3x3-Zahlenfeld. Die Karten, auf denen Terme zu sehen sind, werden offen und für alle gut sichtbar in die Mitte gelegt. Außerdem bekommt jeder und jede einige der Abdeckchips.
Wer an der Reihe ist, würfelt. Die gewürfelte Zahl muss in einen der offen liegenden Terme eingesetzt werden. Der Wert des Terms wird berechnet und allen mitgeteilt (alle sollten überprüfen, ob richtig gerechnet wurde).
Wer das Ergebnis auf dem eigenen Zahlenfeld hat, darf die Zahl mit einem Abdeckchip abdecken. Anschließend wird die verwendete Termkarte umgedreht und die oder der Nächste ist an der Reihe.
Beispiel: Anna würfelt eine 4 und setzt die 4 in den Term 2⋅x+2 ein. Sie erhält 2⋅4+2 = 10. Nun dürfen Anna und die anderen Mitspieler und Mitspielerinnen die 10 auf ihrem Zahlenfeld abdecken, wenn sie eine 10 auf ihren Zahlenfeldern haben. Die Karte mit dem Term 2⋅x+2 wird umgedreht und der oder die Nächste ist mit Würfeln an der Reihe.
Wer zuerst drei Abdeckplättchen in einer Reihe (waagerecht, senkrecht oder diagonal) auf dem eigenen Zahlenfeld liegen hat, gewinnt. Habt ihr alle Terme verwendet (und umgedreht) und es hat noch niemand gewonnen, werden alle Terme auf die Vorderseite zurück gedreht und können wieder benutzt werden.
Wenn du alleine spielst, versuche so schnell wie möglich 3 Plättchen in einer Reihe zu erreichen.
https://editor.mnweg.org/entdecken/dokument/baustein-terme
Termgleichheit - Terme haben viele Gesichter
Um gut mit Termen arbeiten zu können, ist es wichtig zu verstehen, dass der gleiche Term oft auf viele verschiedene Arten und Weisen aufgeschrieben werden kann.
Zum Beispiel können die Malpunkte zwischen Zahlen und Variablen weggelassen werden. Statt 5⋅a kann man also auch 5a schreiben. Die neue Schreibweise wird (wie vorher) 5 mal a
oder nur 5 a
ausgesprochen.
Aber du kennst noch weitere Möglichkeiten, Terme unterschiedlich aufzuschreiben. Die folgende Aufgabe hilft dir, dich zu erinnern.

Im Folgenden können immer mehrere Antworten richtig sein!


https://editor.mnweg.org/entdecken/dokument/baustein-terme

https://editor.mnweg.org/entdecken/dokument/baustein-terme
Terme beschreiben - Mit Termen reden
Terme helfen uns Situationen oder Zustände mathematisch auszudrücken. In unserer Alltagssprache haben wir aber viele unterschiedliche Wörter für die einzelnen Rechenoperationen.
Die folgenden Aufgaben helfen dir dabei, in Zukunft Situationen und Geschichten besser mit Termen beschreiben zu können.
Alltagssprache: Nimm 3 von 7 weg.
Passender Term: 7 - 3
Rechenoperation
Beschreibungen
Addition
Fachbegriff: addieren
+
zusammenrechnen,
Subtraktion
Fachbegriff: subtrahieren
-
wegnehmen,
Multiplikation
Fachbegriff: multiplizieren
⋅
Division
Fachbegriff: dividieren
:
hinzuzählen, zusammenrechnen, dazuzählen, aufteilen, Differenz bilden, zusammenzählen, Quotient bilden, dazurechnen, vervielfältigen, teilen, abziehen, Summe bilden, vermindern, summieren, wegnehmen, hinzufügen, Produkt bilden, zerteilen, abrechnen, zerlegen, malnehmen, zusammenziehen, vervielfachen, trennen, ....
https://editor.mnweg.org/entdecken/dokument/baustein-terme
Die Aufgaben in den roten Zeilen sind besonders knifflig! Verwende dein Arbeitsblatt zum Bearbeiten der Aufgabe.
Beschreibung
+
:
-
⋅
Term
Vermindere 10 um 2.
X
10-2
Verdopple a.
Subtrahiere 6 von f.
Vermindere eine unbekannte Zahl um 10 und nimm 2 dazu.
Ziehe Sieben von einer unbekannten Zahl ab und vervielfache das Ergebnis um 2.
Teile y in zwei gleich große Teile auf.
Bilde die Summe aus einer unbekannten Zahl und einer anderen unbekannten Zahl, welche mit 2 multipliziert wurde.
6+11
Ziehe von a drei ab.
X
a-3
4p
(a-3) ⋅ 2
14-(7:b)
y:2+4x-9
https://editor.mnweg.org/entdecken/dokument/baustein-terme
Termdomino
Hole dir das Material von deiner Lernbegleitung und suche dir einen Partner oder eine Partnerin. Du kannst das Spiel aber auch alleine spielen. Spielt höchstens 30 Minuten.
Zum Spielen braucht ihr:
eines der beiden Termdominos (das lilafarbene Termdomino ist eine Herausforderung, wählt dieses, falls ihr euch im Umgang mit Termen schon sicher fühlt)
Spielanleitung:
Auf den Dominoblättern stehen entweder konkrete Terme oder Beschreibungen von Termen. Jede Hälfte eines Dominoblattes gehört zu der Hälfte eines anderen Dominoblattes.
Du musst je nachdem die Beschreibungen in Terme oder die Terme in Beschreibungen umwandeln. Ordne dann die Dominoblätter passend zu den Lösungen aneinander. Das Spiel ist vorbei, wenn du alle Dominoblätter angelegt hast.
Vergleiche am Ende deine Lösung mit den Lösungen deiner Lernbegleitung.
https://editor.mnweg.org/entdecken/dokument/baustein-terme
Terme im Alltag - Mit Termen Geschichten erzählen
Bisher hast du dich intensiv mit dem Bauen und Beschreiben von Termen beschäftigt. Die bisherigen Aufgaben klangen dabei sehr mathematisch...
Nun wollen wir uns mit Beschreibungen aus dem Alltag beschäftigen! In den nächsten Aufgaben übst du, wie man aus alltäglichen Geschichten und Situationen Terme baut.
Wie groß ist Emre, wenn Karl 153 cm groß ist? Antwort:
Wie viel wiegt Sarah, wenn Kerstin 53 kg schwer ist? Antwort:
c) Finde einen möglichen Term um die folgende Geschichte mathematisch zu beschreiben.
Antwort:
Antwort:
Wie viel müsste eine Familie mit x Erwachsenen und y Kindern bezahlen?
Antwort:
Ich habe so viele Bücher rumstehen, ich gebe dir welche. Dann hast du doppelt so viele wie jetzt. Wie viele Bücher hat Clara jetzt?
Antwort:
https://editor.mnweg.org/entdecken/dokument/baustein-terme
Von den Einnahmen auf einem Flohmarkt müssen immer 8 € Standgebühr bezahlt werden.
Dividiere eine beliebige Zahl durch 8.
x + 8
Die Bezahlung von jedem Auftritt wird gleichmäßig an die 8 Bandmitglieder verteilt.
x : 8
Von einer beliebigen Zahl 8 subtrahieren.
8 - x
Martina verdient beim Kellnern 8 € pro Stunde und bekommt zusätzlich noch unterschiedlich viel Trinkgeld.
Addiere 8 zu einer beliebigen Zahl.
x - 8
Eine beliebige Zahl von 8 abziehen.
Die Zahl der Kinder in der Reitgruppe ist von Woche zu Woche verschieden, da immer unterschiedlich viele der 8 Kinder fehlen.
https://editor.mnweg.org/entdecken/dokument/baustein-terme
- Alyia hat ein Angebot für einen Handyvertrag gefunden. Die Grundgebühr beträgt 5€ und der Preis pro telefonierte Minute 15 Cent. Die monatlichen Kosten kann man mit dem folgenden Term berechnen.
Trage ein, für was die Zahlen und Variablen in diesem Term stehen.
Setze ein.
(1) Anzahl der Gesprächsminuten
(2) monatliche Kosten
(3) Grundgebühr
(4) Preis pro Minute
A = 5 + 0,15x
Minuten
5
10
20
50
75
100
A
5 + 0,15 ⋅ 5 = ...
...die Grundgebühr 10 € beträgt?
...der Preis pro telefonierte Minute 7 Cent beträgt?
https://editor.mnweg.org/entdecken/dokument/baustein-terme
Check-Out
Antwort:
Rechne den Term für x = 5 aus. Antwort:
Pia ist 4 cm kleiner als Maria. Wie groß ist Pia? Antwort:
Antwort:
Wie viele Bücher hat Markus, wenn Amara 29 Bücher hat.
Antwort:

Im Folgenden können immer mehrere Antworten richtig sein!

https://editor.mnweg.org/entdecken/dokument/baustein-terme
Blomberg, Judith; Abshagen, Maike: Arbeitsheft: Mathe-Welt : Fit in Algebra? Mach den smart-Test!. In: mathematik lehren Jg. 202 / 2017, Heft 3; Hannover: Friedrich Verlag
mathematik lehren Jg. 136 / 2006, Heft 3; Hannover: Friedrich Verlag
mathematik lehren Jg. 202 / 2017, Heft 3; Hannover: Friedrich Verlag
Termbingo aus dem Methekoffer Algebra von MUED
https://editor.mnweg.org/entdecken/dokument/baustein-terme


