Frau Weiß möchte eine 4-Zimmer-Wohnung mieten. Bei der Besichtigung misst sie die Zimmer aus und berechnet die gesamte Wohnfläche:

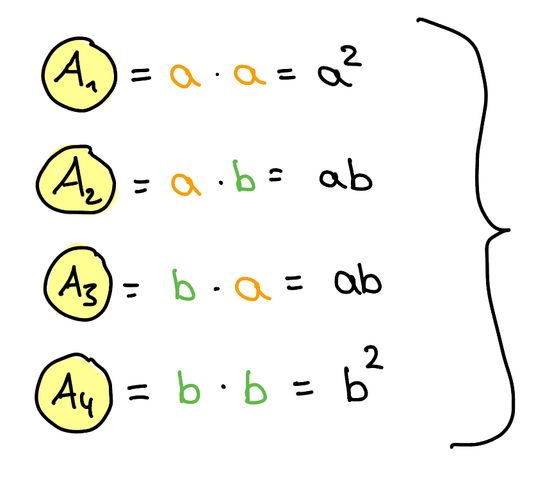
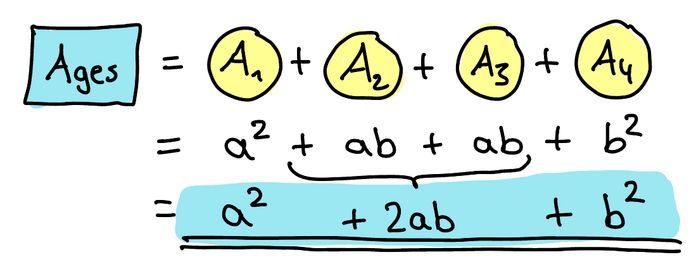
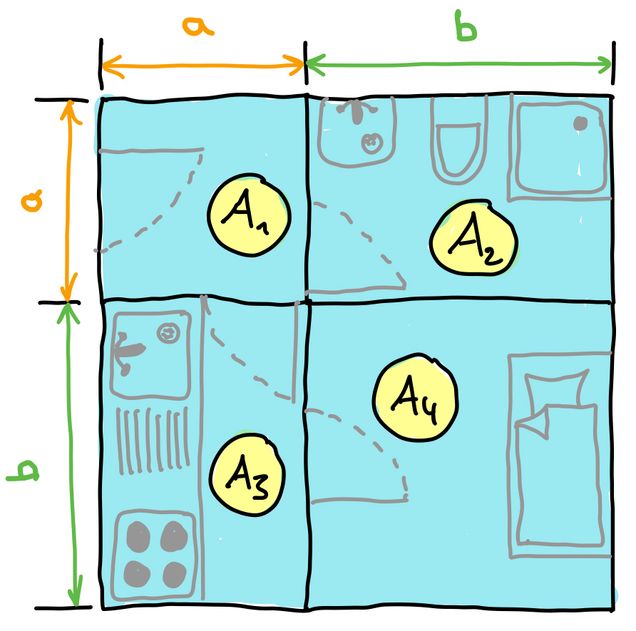
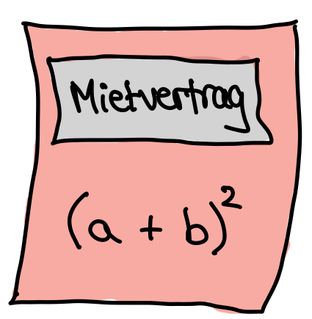
Im Mietvertrag steht folgende Wohnfläche der Wohnung:

Eingangsfrage

Was ist richtig, die Angabe im Mietvertrag oder die Berechnung von Frau Weiß?

Rechenweg

Die Formel im Mietvertrag kannst du mit sich selbst ausmultiplizieren:

a \cdot a = a^{2} a + a = 2 a

Erklärvideo

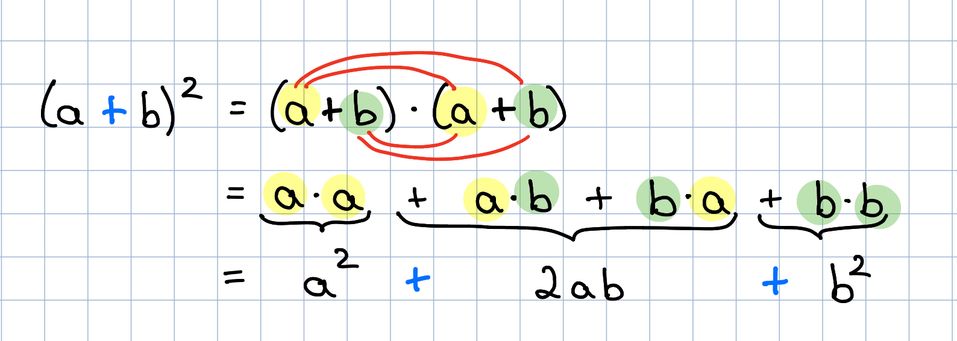
Schau das

Video an:

Antwort

Beide Angaben sind richtig.

Merke

Die 1. binomische Formel ist:

(a + b)^{2} = a^{2} + 2 ab + b^{2}

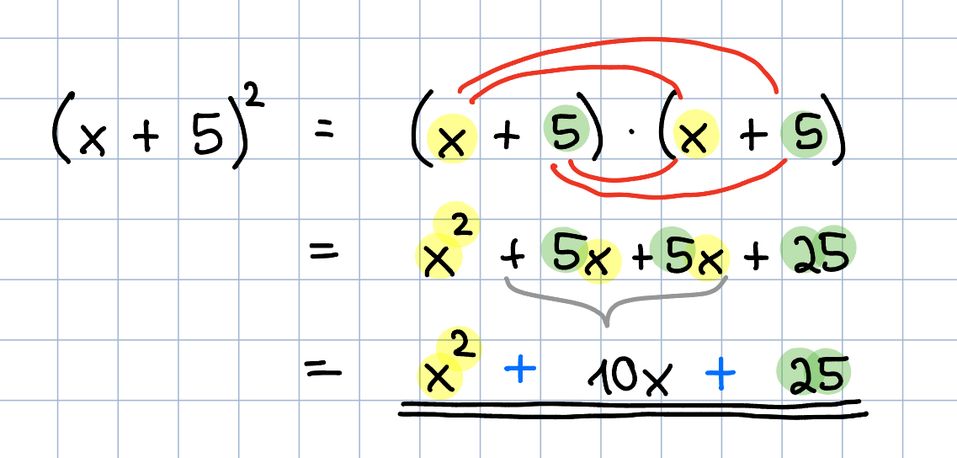
Beispiel:

Löse alle Aufgaben auf einem karierten Block-Blatt (und nicht in den grauen Feldern!).

1

Ergänze die Lücken.

(7y+9z)² = + 126zy + 81z²
(3+5x) (3+5x) = 9 + + 25x²
(5y+6z)² = + 60zy + 36z²
(5y+2z)² = + 20zy + 4z²
(2+7x) (2+7x) = 4 + + 49x²
( +3x)² = 81 + 54x + 9x²
(9y+10z) (9y+10z) = 81y² + 180zy +
(6y+2z) (6y+2z) = 36y² + 24zy +

2

Verbinde richtig:

(x+11)²
(x+1)²
(7+x)²
(x+15)²
(x+5)²

= (x+1)(x+1)
= x² + 22x + 121
= 49 + 14x + x²
= (x+5)(x+5)
= (x+15)(x+15)

3

Vereinfache die Terme mit Hilfe der ersten binomischen Formel.

(4x+3)² =
(4+7x)² =
(3+3x)² =
(1x+6)² =
(9x+7)² =
(5+5x)² =

4

Ordne zu:

(19+x)(19+x)
(x+2)(x+2)
(x+13)(x+13)
(4+x)(4+x)
(x+5)(x+5)

= x² + 4x + 4
= 324+ 38x + x²
= 16 + 8x + x²
= (x+5)²
= x² + 26x + 169

5

Multipliziere die Terme mit Hilfe der ersten binomischen Formel aus.

(9y+6z)² =
(8y+10z)² =
(4y+6z)² =
(2y+1z)² =
(4y+3z)² =
(4y+9z)² =

6

Wirst du Millionär?

Herr Cool möchte eine 3-Zimmer-Wohnung mieten.

Bei der Besichtigung berechnet er für das Schlafzimmer folgende Fläche:

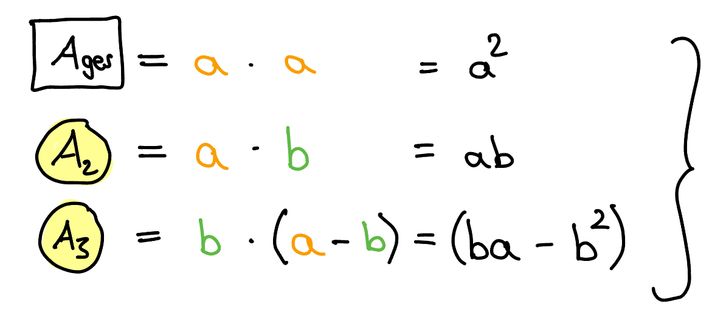
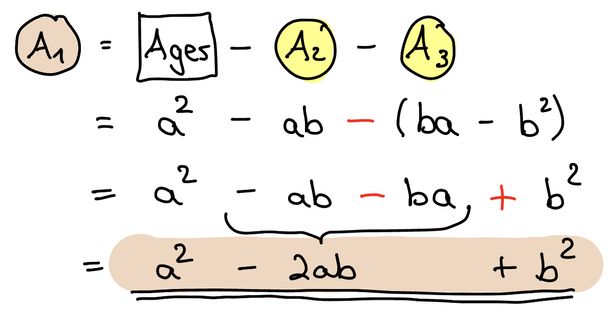
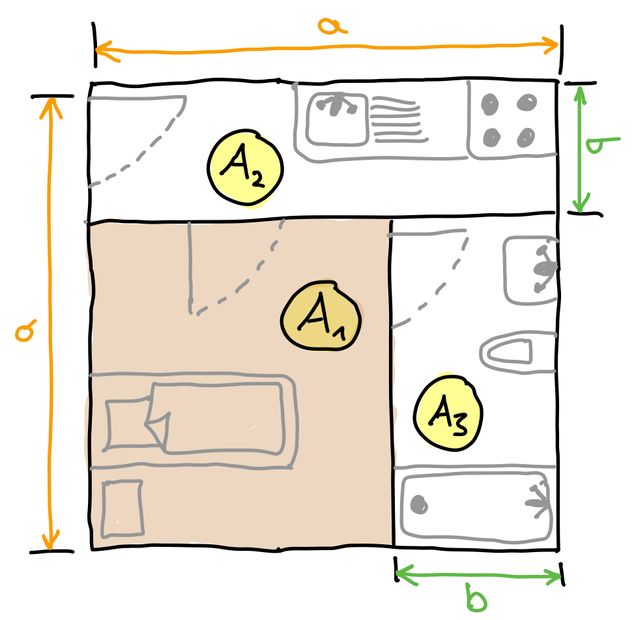
Im Mietvertrag steht aber folgende Wohnzimmerfläche:

Eingangsfrage

Was ist richtig, die Angabe im Mietvertrag oder die Berechnung von Herr Cool?

Rechenweg

Die Formel im Mietvertrag kannst du mit sich selbst ausmultiplizieren:

Antwort

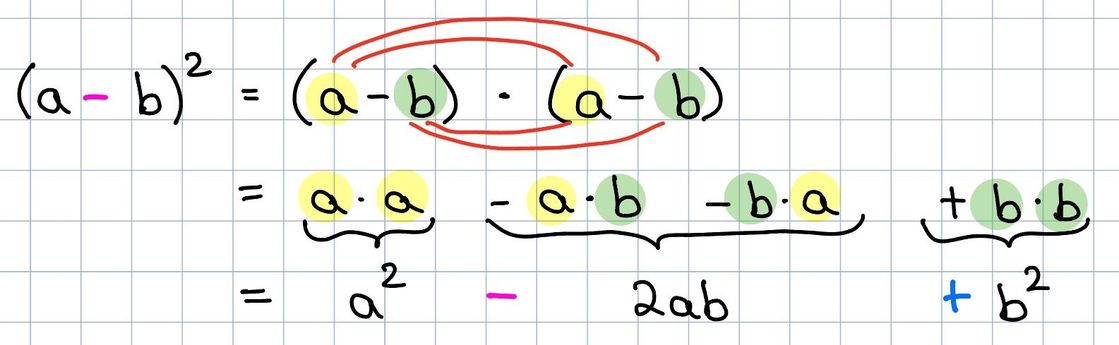
Beide Angaben sind richtig.

Merke

Die 2. binomische Formel ist:

$(a - b)^{2} = 2 a^{2} - 2 ab + b^{2}$

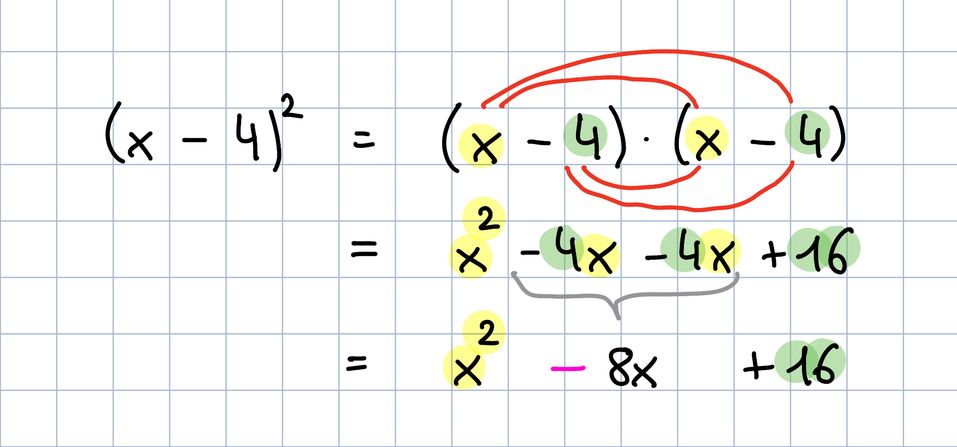
Beispiel:

Löse alle Aufgaben auf einem karierten Block-Blatt (und nicht in den grauen Feldern!).

7

Ergänze die Lücken.

(3y-5z)² = - 30zy + 25z²
( -9x)² = 4 - 36x + 81x²
(6y-8z)² = - 96zy + 64z²
( -5x)² = 16 - 40x + 25x²
(6y-5z) (6y-5z) = 36y² - 60zy +
(5-8x) (5-8x) = 25 - + 64x²
(6y-7z) (6y-7z) = 36y² - 84zy +
(8y-10z)² = - 160zy + 100z²

8

Ordne zu.

(19-x)(19-x)
(x-3)(x-3)
(x-13)(x-13)
(6-x)(6-x)
(x-1)(x-1)

= x² - 6x + 9
= 324- 38x + x²
= 36 - 12x + x²
= (x-1)²
= x² - 26x + 169

9

Vereinfache die Terme mit Hilfe der zweiten binomischen Formel.

(4-4x)² =
(6x-8)² =
(9x-4)² =
(4x-6)² =
(3-6x)² =
(3x-8)² =

10

Verbinde richtig.

(x-5)²
(x-12)²
(x-3)²
(x-15)²
(9-x)²

= (x-3)(x-3)
= x² - 24x + 144
= 81 - 18x + x²
= (x-5)(x-5)
= (x-15)(x-15)

11

Multipliziere die Terme mit Hilfe der zweiten binomische Formel aus.

(4y-9z)² =
(2y-5z)² =
(10y-4z)² =
(5y-3z)² =
(7y-7z)² =
(3y-3z)² =

12

Wirst du Millionär?

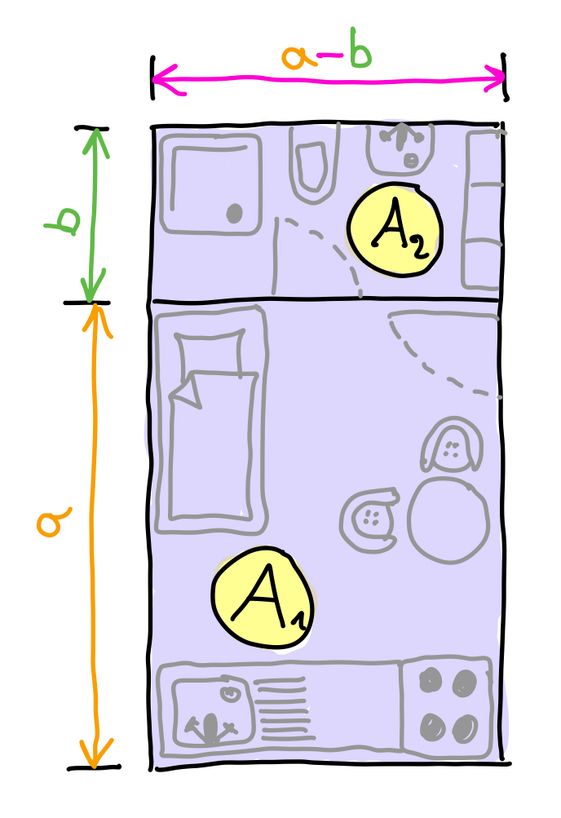
Clara mietet ihre erste eigene 2-Zimmer-Wohnung.

Beim Einzug misst sie die Zimmer aus und berechnet für die gesamte Wohnfläche:

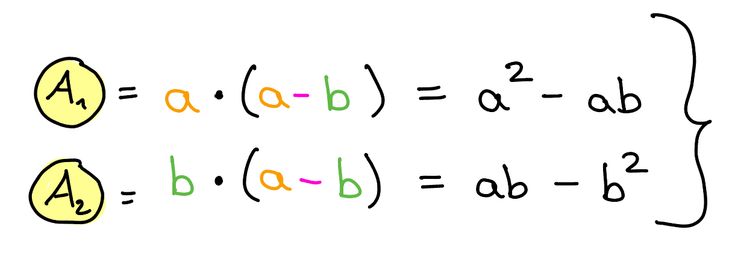
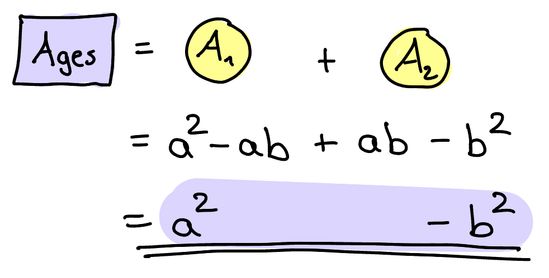
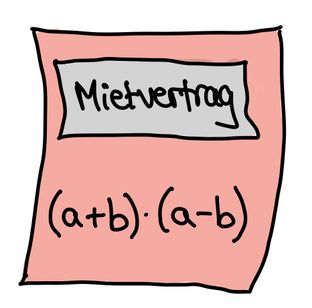
Im Mietvertrag steht folgende Wohnfläche der Wohnung:

Eingangsfrage

Was ist richtig, die Angabe im Mietvertrag oder die Berechnung von Clara?

Rechenweg

Die Formel im Mietvertrag kannst du mit sich selbst ausmultiplizieren:

Erklärvideo

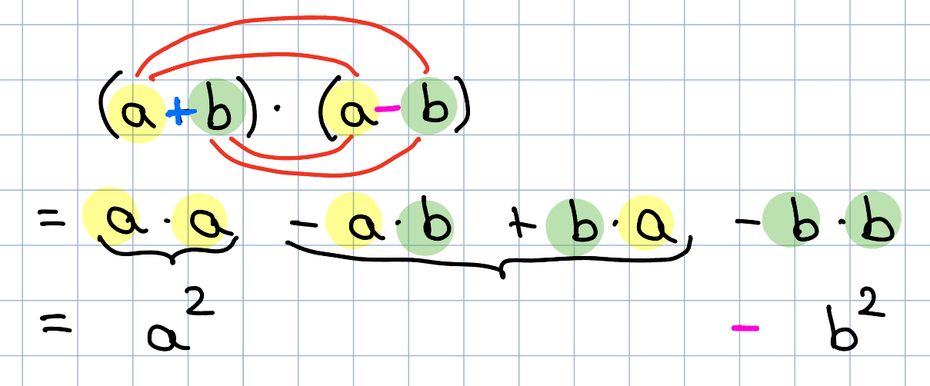
Schau das

Video an:

Antwort

Beide Angaben sind richtig.

Merke

Die 3. binomische Formel ist:

(a + b) (a - b) = a^{2} - b^{2}

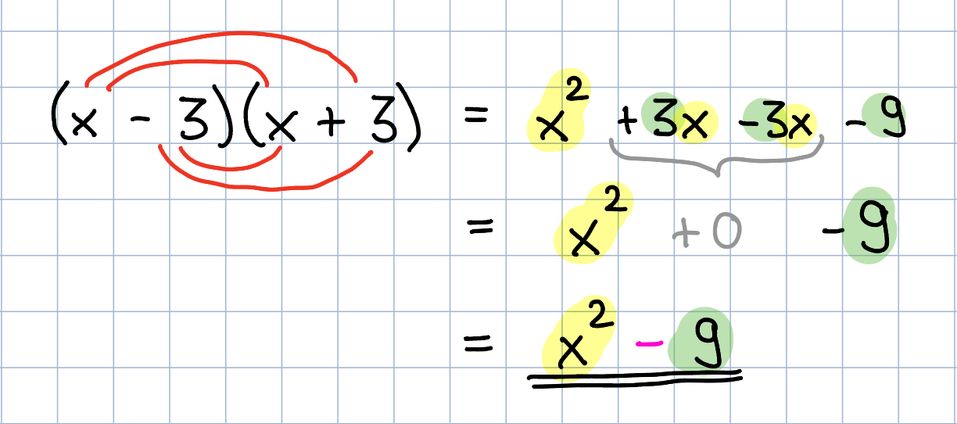
Beispiel:

Löse alle Aufgaben auf einem karierten Block-Blatt (und nicht in den grauen Feldern!).

13

Ergänze die Lücken.

(3y-2z) (3y+2z) = - 4z²
(7y+4z) (7y-4z) = 49y² -
(9y+4z) (9y-4z) = 81y² -
(6-3x) (6+3x) = - 9x²
(10y-8z) (10y+8z) = - 64z²
(2-3x) (2+3x) = - 9x²
(8y-7z) (8y+7z) = - 49z²
( -7x) ( +7x) = 64 - 49x²

14

Verbinde richtig:

64 - x²
x² -12²
(x-3)(x+3)
(x+1)(x-1)
x² - 225

=x² - 9
= (x-12)(x+12)
= (x-15)(x+15)
= (8-x)(8+x)
=x² - 1

15

Vereinfache die Terme mit Hilfe der dritten binomischen Formel.

(10+4x) (10-4x) =
(1x+5) (1x-5) =
(7x-3) (7x+3) =
(3-5x) (3+5x) =
(8x-5) (8x+5) =
(1+9x) (1-9x) =

16

Ordne zu:

(17-x)(17+x)
(x+4)(x-4)
(x-13)(x-13)
(6-x)(6+x)
(x-1)(x+1)

= x² - 16
= 289 - x²
= 36 - x²
= x²-1²
= x² - 169

17

Multipliziere die Terme mit Hilfe der dritten binomischen Formel aus.

(10y-4z)(10y+4z) =
(8y-8z)(8y+8z) =
(5y+7z)(5y-7z) =
(9y-7z)(9y+7z) =
(3y-9z)(3y+9z) =
(5y+6z)(5y-6z) =

Löse alle Aufgaben auf einem karierten Block-Blatt (und nicht in den grauen Feldern!).

18

Um welche binomische Formel handelt es sich? Kreuze an.
Vorsicht: Es haben sich Terme eingeschlichten, welche keine binomische Formel sind.

1. binom. Formel

2. binom. Formel

3. binom. Formel

keine binom. Formel

(x + 2)²

(7 - y)²

(8 + 2x)²

(a - b)(a + b)

4x² - 16x + 16

(5u - z)(5u + z)

2x²-8x²-6x²

49x² - 81y²

36 + 12x + x²

21x³-4x+8

19

Scanne den QR-Code und begebe dich auf die Fehlersuche! Überprüfe, ob die Gleichungen richtig sind und ordne sie dann entsprechend zu.

20

Was wurde hier falsch gemacht?
Beschreibe den Fehler und schreibe das richtige Ergebnis auf.

(x + 8)² = x² + 64
(a - 5)² = a² - 10a - 25
(10 + 2x)² = 100 + 40x + 2x²
(x - 9)² = x² - 9x + 81

21

Gib jeweils den Flächeninhalt der Quadrate mit einer binomischen Formel an. Um welche binomische Formel handelt es sich?

22

Scanne den QR-Code und ordne jedem blau markierten Kärtchen das passende orange markierte Kärtchen zu.