HerunterladenAls PDF Herunterladen
  • 2. Strahlensatz Anwendungsaufgaben
  • Deliah Herbstritt
  • 21.07.2020
  • Mathematik
  • Flächen
  • R
  • 9
  • Einzelarbeit
  • Arbeitsblatt
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
2. Strahlensatz Anwendungsaufgaben
Mathematik Flächen R 9
1
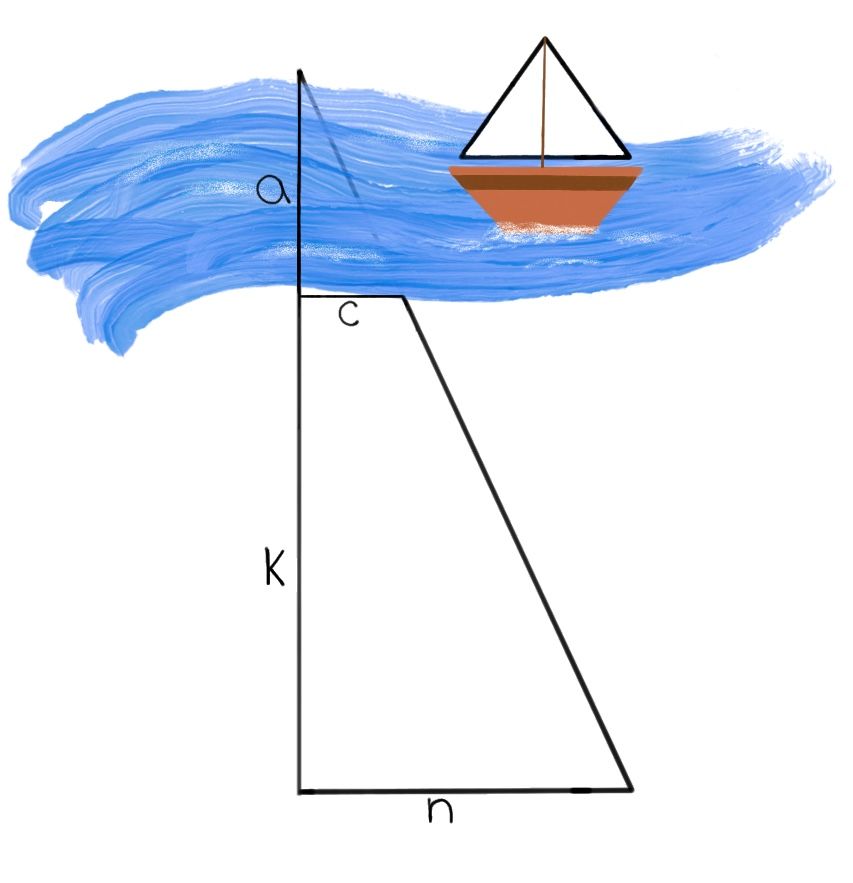
Frida möch­te eine Boots­tour mit ihrem 12m brei­ten Boot durch einen Kanal ma­chen.
Lei­der weiß sie die Brei­te (a) des Ka­nals nicht. Finde nun mit­hil­fe der Gra­fik her­aus, ob Frida mit ihrem Boot durch den Kanal fah­ren kann oder nicht.

k= 11m

c= 28m

n= 20m

Lösung1
ac=kn\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \frac{a}{c}=\frac{k}{n}

a28m=11m20m\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \frac{a}{28m}=\frac{11m}{20m} ∣⋅28m\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} |\cdot28m

a=11m20m⋅28m\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} a=\frac{11m}{20m}\cdot28m

a=15,4m\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} a=15{,}4m

Ant­wort: Frida kann durch den Kanal fah­ren, da der Kanal 15,4m breit ist und ihr Boot nur 12m breit ist.
2
Wie hoch ist ein Baum, der einen 10m lan­gen Schat­ten wirft, wenn gleich­zei­tig der Schat­ten eines 1,70m gro­ßen Man­nes, 1,23m lang ist?
Mache Skiz­ze und löse die Auf­ga­be.
Lösung2
Zeige die Skiz­ze dei­nem Lern­be­glei­ter!

h Baum10m=170m1,23m\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \frac{h\,Baum}{10m}=\frac{170m}{1{,}23m} ∣⋅10m\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} |\cdot10m

h\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} h Baum=1,70m1,23m⋅10m\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} =\frac{1{,}70m}{1{,}23m}\cdot10m

h\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} h Baum=11,38m\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} = 11{,}38m

Ant­wort: Der Baum ist 11,38m hoch.
Bereitgestellt von: Deliah Herbstritt Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/c536acae
Seite: 1/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/c536acae
AB
2. Strahlensatz Anwendungsaufgaben
Mathematik Flächen R 9
3
Ein Cock­tail­to­ma­te von 3cm Durch­mes­ser ver­deckt ge­ra­de den 9m brei­ten Au­to­tun­nel, wenn man sie un­ge­fähr 50cm vom Auge ent­fernt hält. Wie weit ist der Tun­nel ent­fernt?
Eine Skiz­ze kann dir hel­fen.
Lösung3
9mEntfernung=0,03m0,5m\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \frac{9m}{Entfernung}=\frac{0{,}03m}{0{,}5m} ∣⋅\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} |\cdotEnt­fer­nung

9m=0,03m0,5m⋅\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} 9m=\frac{0{,}03m}{0{,}5m}\cdotEnt­fer­nung ∣:(0,03m0,5m)\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} |:(\frac{0{,}03m}{0{,}5m})

9m:(0,03m0,5m)=\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} 9m:(\frac{0{,}03m}{0{,}5m})=Ent­fer­nung

150m=\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} 150m=Ent­fer­nung

Ant­wort: Der Tun­nel ist 150m ent­fernt.
4
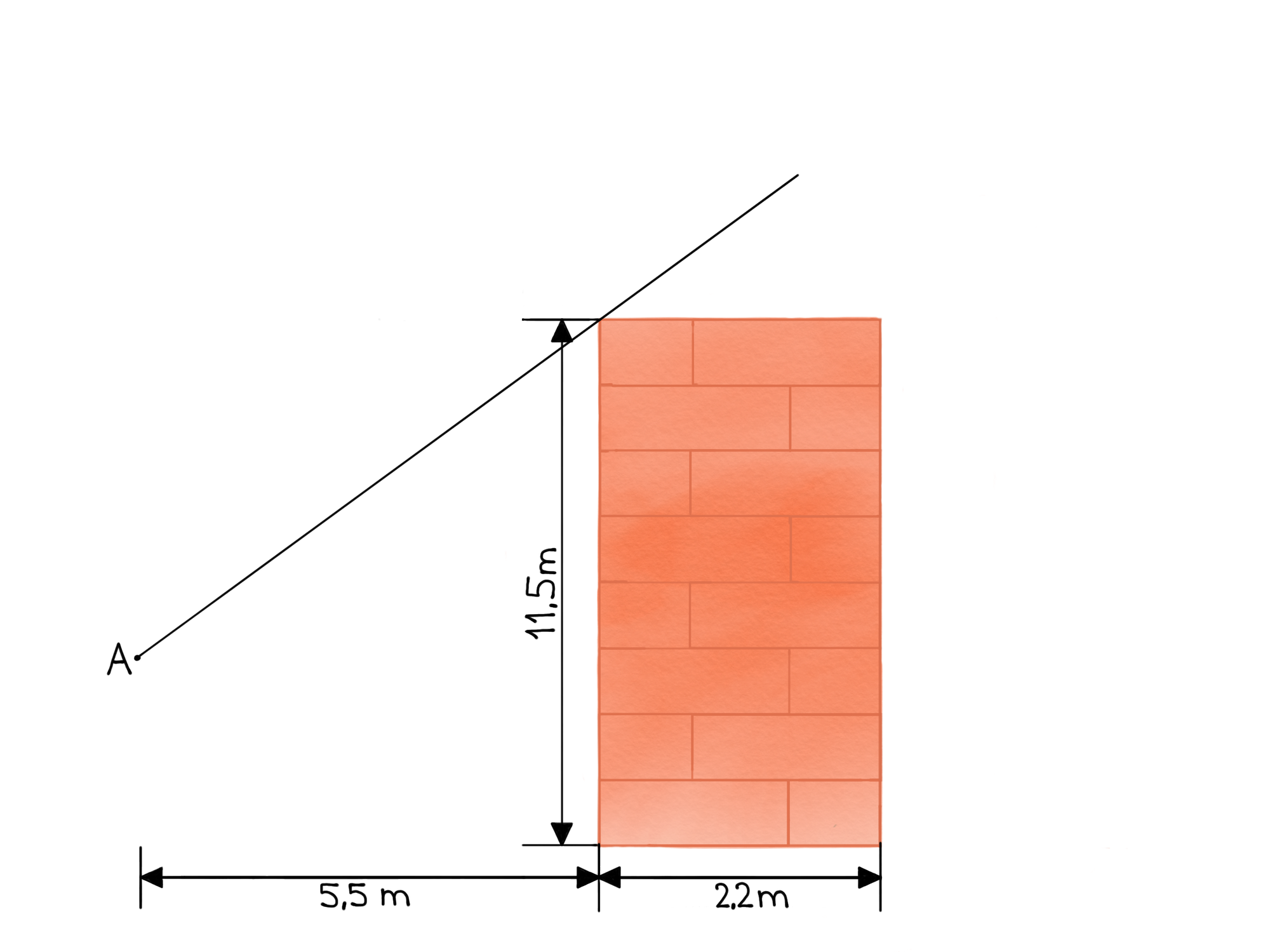
Mar­lon läuft an der Kir­che vor­bei. Von B aus kann er ge­ra­de noch die Spit­ze des Kirch­turms sehen, der di­rekt hin­ter der Mauer steht. Wie hoch ist der Turm min­des­tens?
Lösung4
Kirchturm7,7m=11,5m5,5m\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \frac{Kirchturm}{7{,}7m}=\frac{11{,}5m}{5{,}5m} ∣⋅7,7m\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} |\cdot7{,}7m

Kirch­turm =11,5m5,5m⋅7,7m\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} =\frac{11{,}5m}{5{,}5m}\cdot7{,}7m

Kirch­turm =16,1m\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} =16{,}1m

Ant­wort: Der Kirch­turm ist min­des­tens 16,1m groß.
Bereitgestellt von: Deliah Herbstritt Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/c536acae
Seite: 2/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/c536acae
x