Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
X-Figur Übungen
Mathematik Flächen R 9
1
Berechne die fehlende Strecke x.
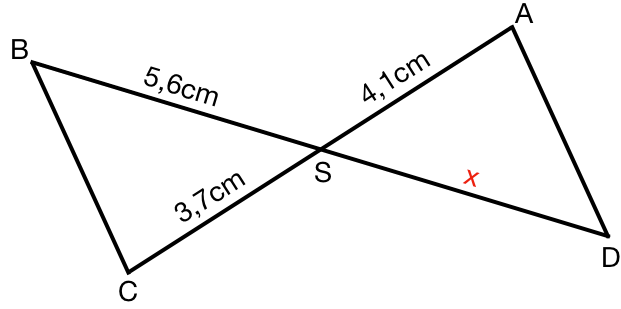
2
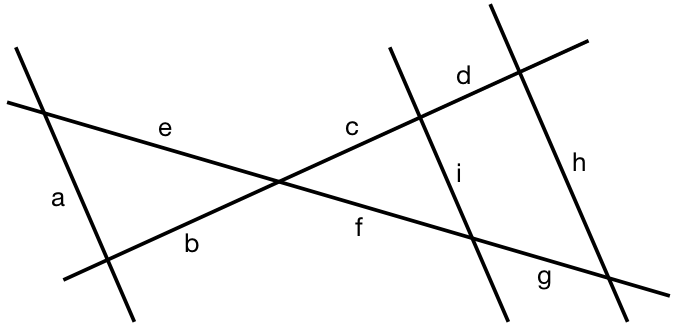
Ergänze zu der Strahlensatzfigur die Verhältnisgleichungen so oft wie vorgegeben.
cc+d = ff+g
c+dh = ci
hi = g+ff
fc = f+gc+d
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/d3c2f65f
https://editor.mnweg.org/entdecken/dokument/d3c2f65f
AB
X-Figur Übungen
Mathematik Flächen R 9
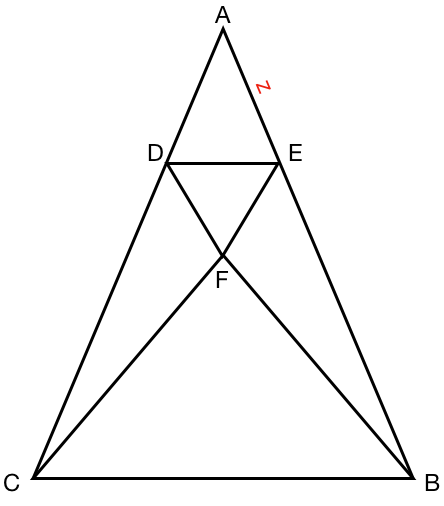
3
Berechne z mithilfe der Strahlensatzgleichung. Markiere die gegebenen Seiten in der Figur farbig.
Gegeben:
AB=8,1cm
DB=6,6cm
DE=1,9cm
EB=4,8cm
EF=1,3cm
CB=5,9cm
DC=4,6cm
AD=2,6cm
DB=6,6cm
DE=1,9cm
EB=4,8cm
EF=1,3cm
CB=5,9cm
DC=4,6cm
AD=2,6cm
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/d3c2f65f
https://editor.mnweg.org/entdecken/dokument/d3c2f65f


