HerunterladenAls PDF Herunterladen
  • Grundaufgaben Pythagoras
  • Deliah Herbstritt
  • 21.07.2020
  • Mathematik
  • Flächen
  • R (Regelstandard)
  • 9
  • Einzelarbeit
  • Arbeitsblatt
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
Grundaufgaben Pythagoras
Mathematik Flächen R 9
1
Be­schrif­te die Flä­chen­dia­go­na­le und die Raum­dia­go­na­le.
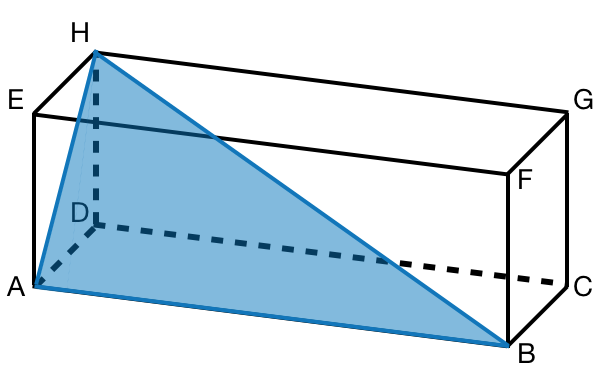
2
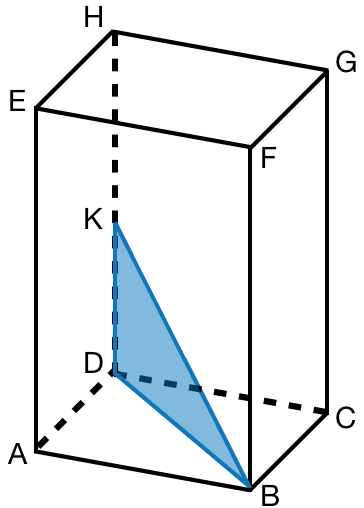
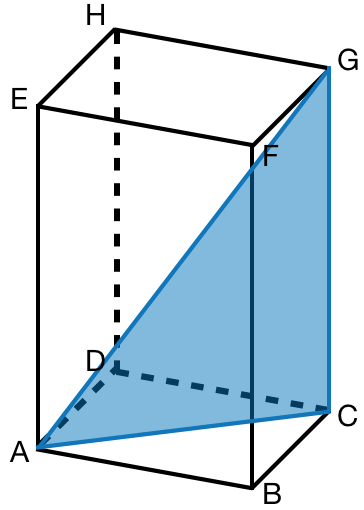
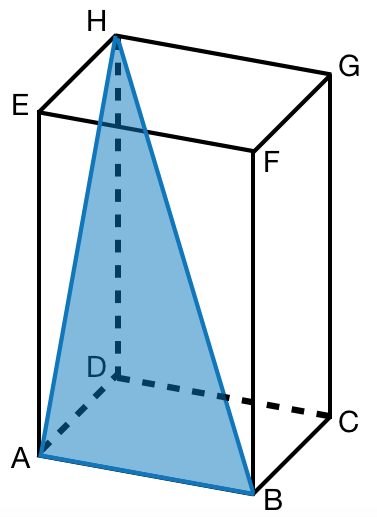
In jedem Qua­der lie­gen ver­schie­de­ne Drei­ecke. Zeich­ne bei den ent­stan­de­nen Drei­ecken rech­te Win­kel ein, die für die Be­rech­nung von Stre­cken nötig wären.
Bereitgestellt von: Deliah Herbstritt Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/d41b93c2
Seite: 1/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/d41b93c2
AB
Grundaufgaben Pythagoras
Mathematik Flächen R 9
3
Be­rech­ne die Raum­dia­go­na­le die­ses Qua­ders.
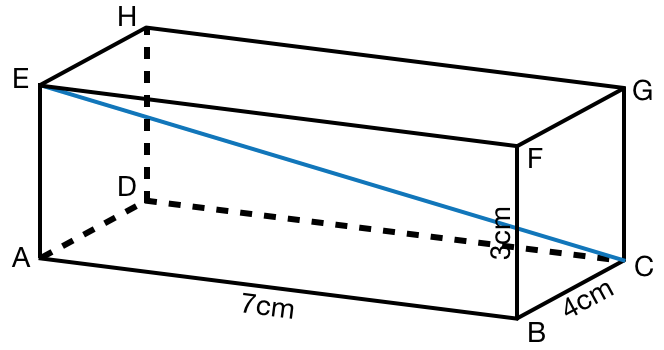
4
Be­rech­ne die Flächen-​/ und Raum­dia­go­na­le fol­gen­der Kör­per. Fer­ti­ge dazu eine Schräg­bild­skiz­ze an.
  • Qua­der mit den Maßen: I= 8cm, b= 4cm, h= 2cm
  • Wür­fel mit der Kan­ten­län­ge a= 3cm
Bereitgestellt von: Deliah Herbstritt Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/d41b93c2
Seite: 2/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/d41b93c2
x