Name: Materialnetzwerk e. G.
Address: Endersstr. 33, Wutöschingen, BW, 79793
Telephone: +49 7746 92 85 70

Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

AB
Strahlensatz anwendbar?
Mathematik Flächen R 9
1
Bei welchem Dreieck ist der Strahlensatz anwendbar (ähnliche Dreiecke)? Gehe vor wie im Beispiel. Wenn du willst kannst du dir die ähnlichen Dreiecke mit einem Buntstift markieren!
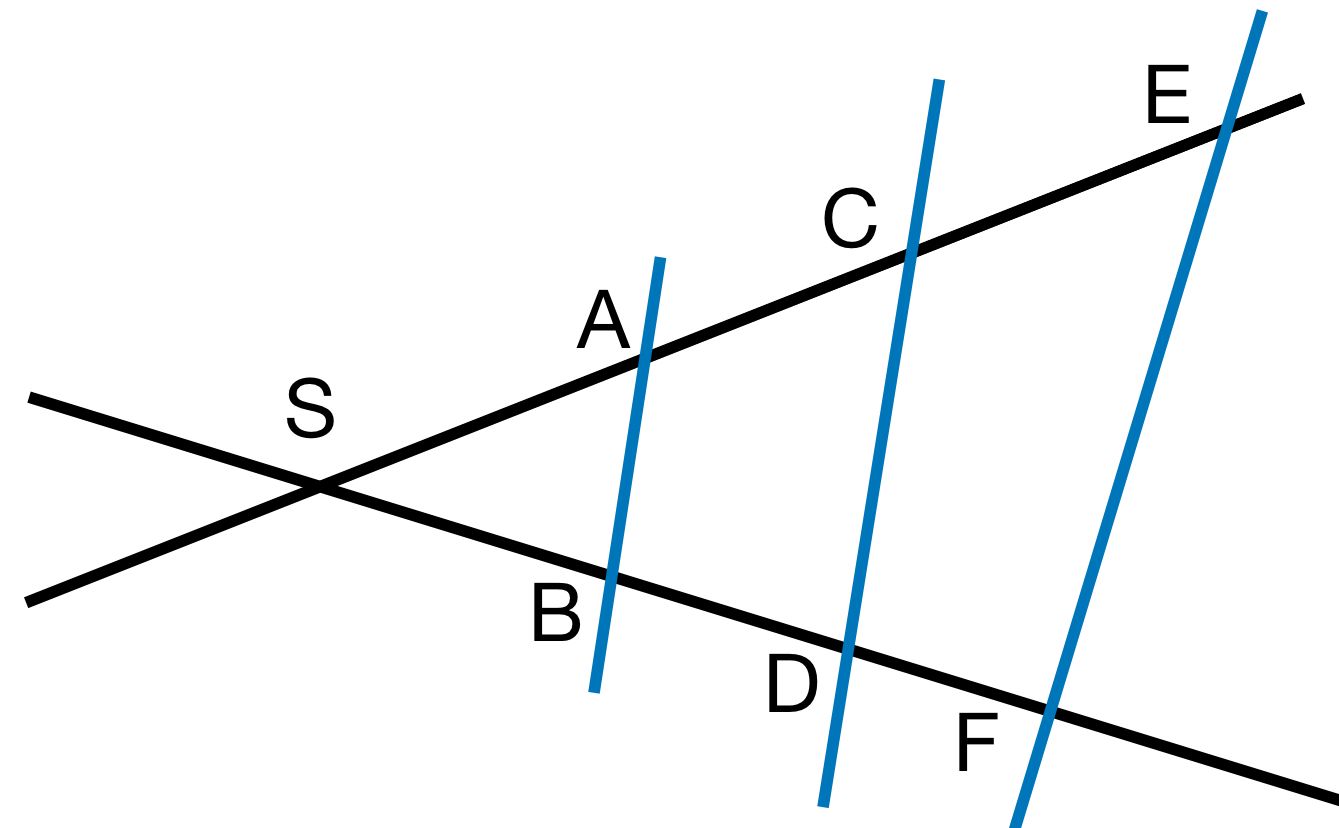
Beispiel:
Es gilt $\gdef\cloze#1{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}} \overline{AB}||\overline{EF}$
( $\gdef\cloze#1{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}} \overline{AB}$ ist parallel $\gdef\cloze#1{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}} \overline{EF}$ )
Die Dreicke SAB und SEF sind ähnlich
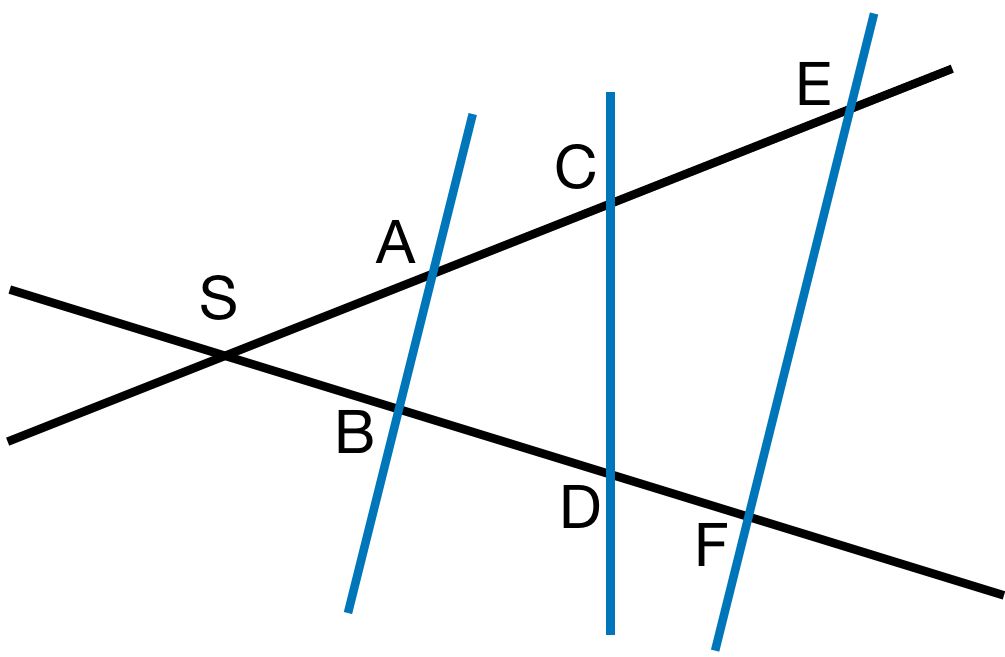
a)
Es gilt: $\gdef\cloze#1{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}} \cloze{\overline{AB}} || \cloze{\overline{EF}}$
Die Dreiecke sind ähnlich.
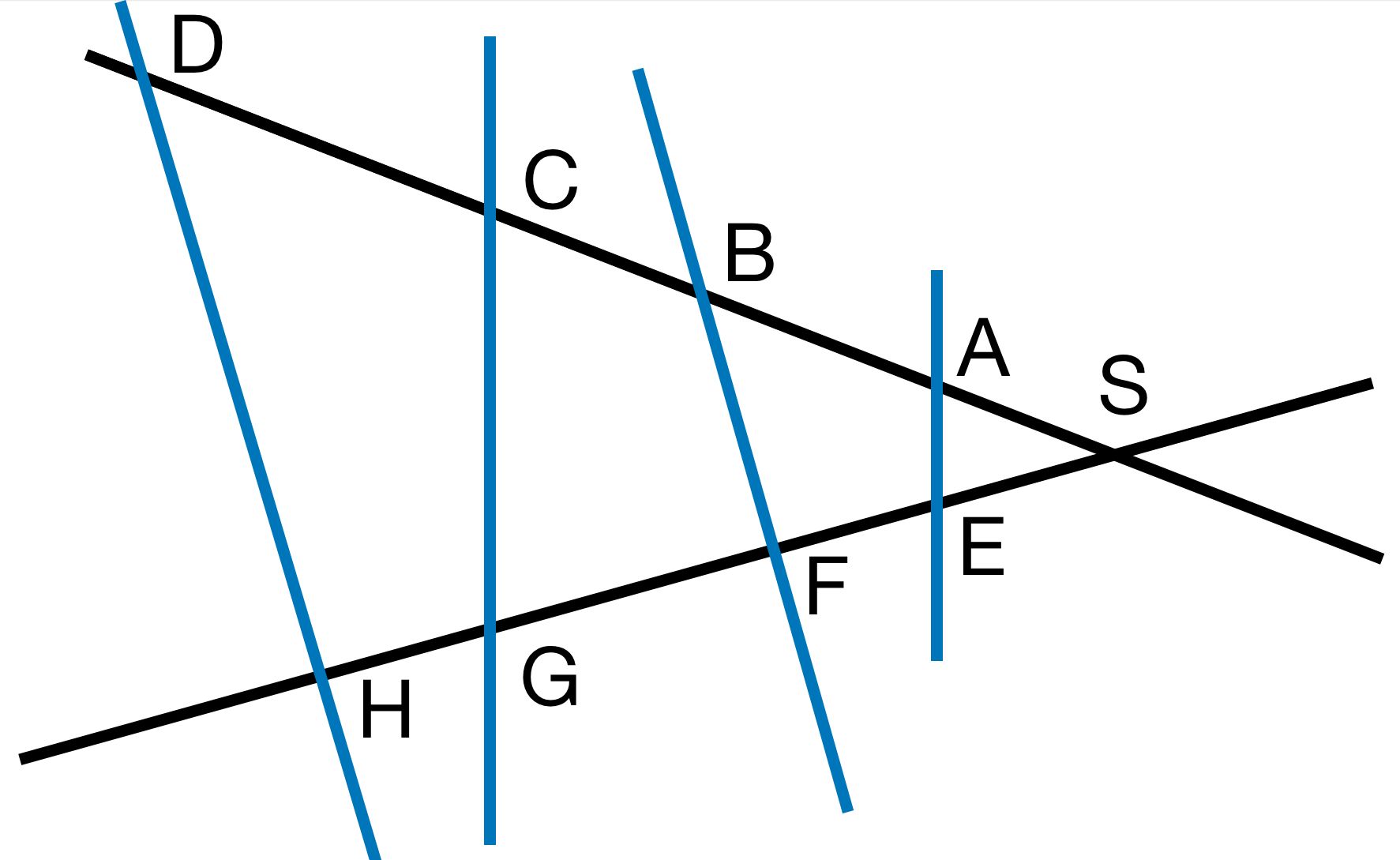
b)
Es gilt: $\gdef\cloze#1{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}} \cloze{\overline{AE}} || \cloze{\overline{CG}}$ und $\gdef\cloze#1{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}} \cloze{\overline{BF}} || \cloze{\overline{DH}}$
Die Dreiecke sind ähnlich und die Dreiecke sind ähnlich.
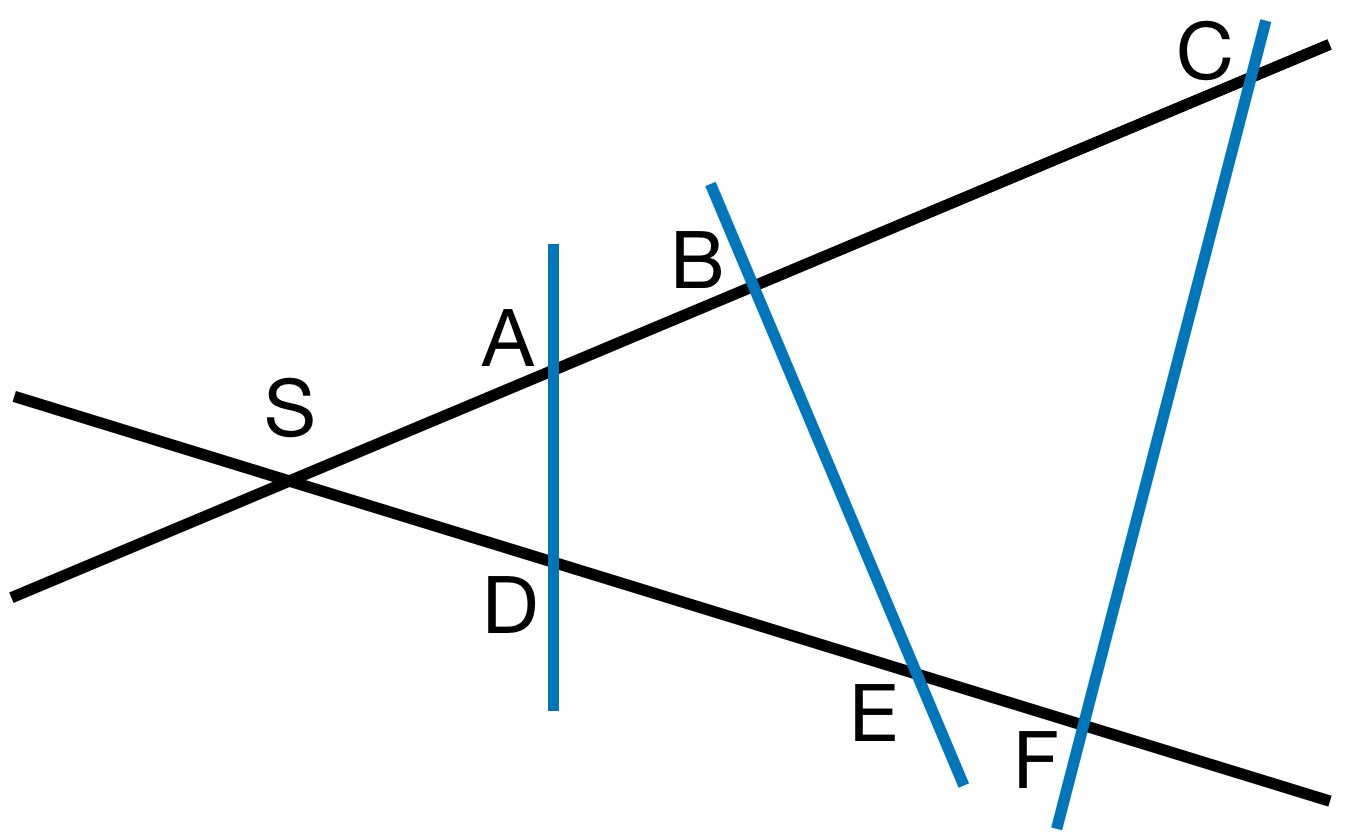
c)
Es gilt:
Die Dreiecke
Bereitgestellt von: Deliah Herbstritt Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/de0a5ca6
Seite: 1/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/de0a5ca6
AB
Strahlensatz anwendbar?
Mathematik Flächen R 9
2
Überprüfe nun rechnerisch, ob der Strahlensatz anwendbar ist und gehe dann wie im Beispiel vor!
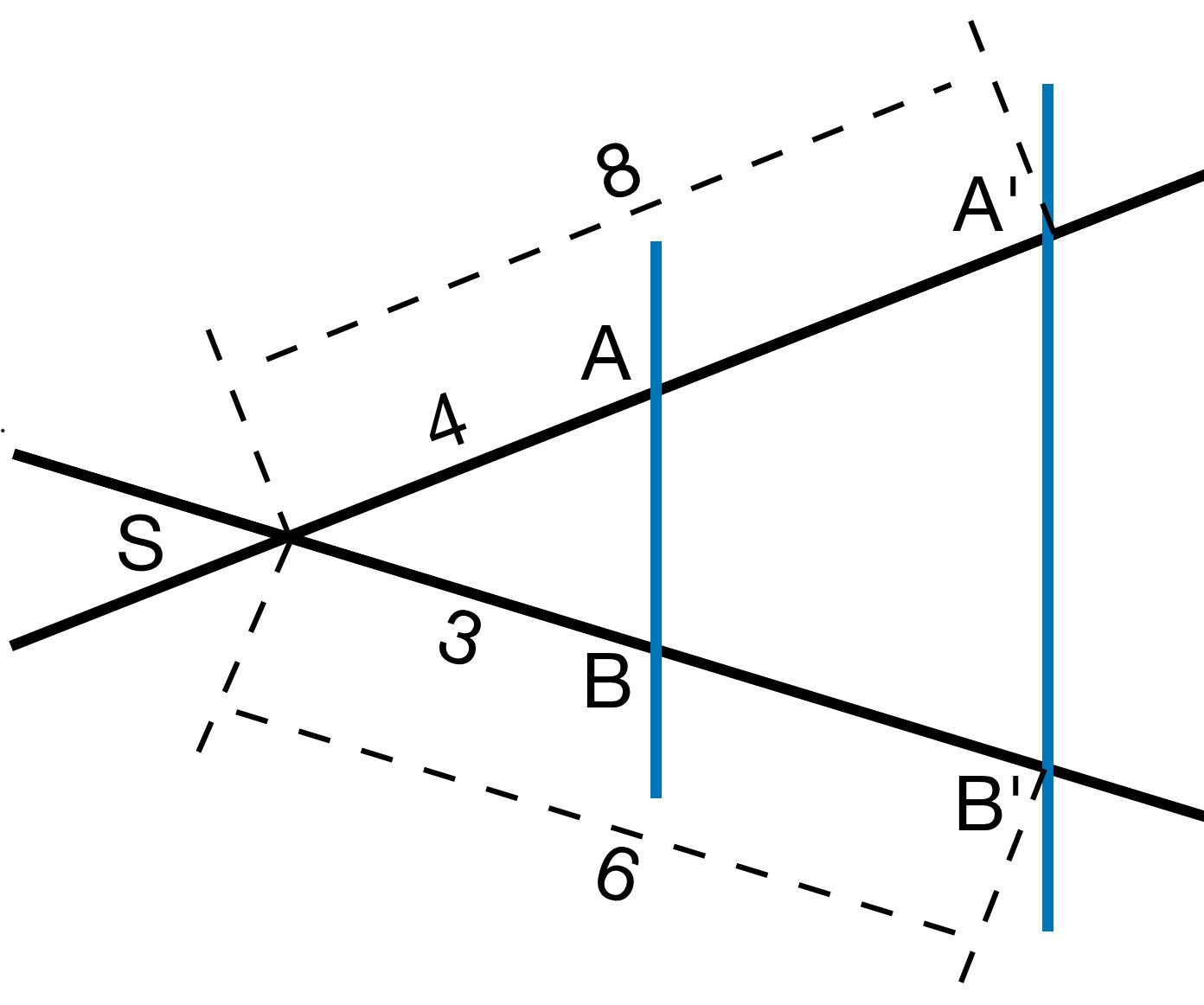
Beispiel:
$\gdef\cloze#1{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}} \frac{\overline{SA'}}{\overline{SA}}=\frac{\overline{SB'}}{\overline{SB}}$

$\gdef\cloze#1{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}} \frac{8}{4}=\frac{6}{3}=2$
Der Strahlensatz ist anwendbar, da die Seitenlängen im gleichen Verhältnis stehen.
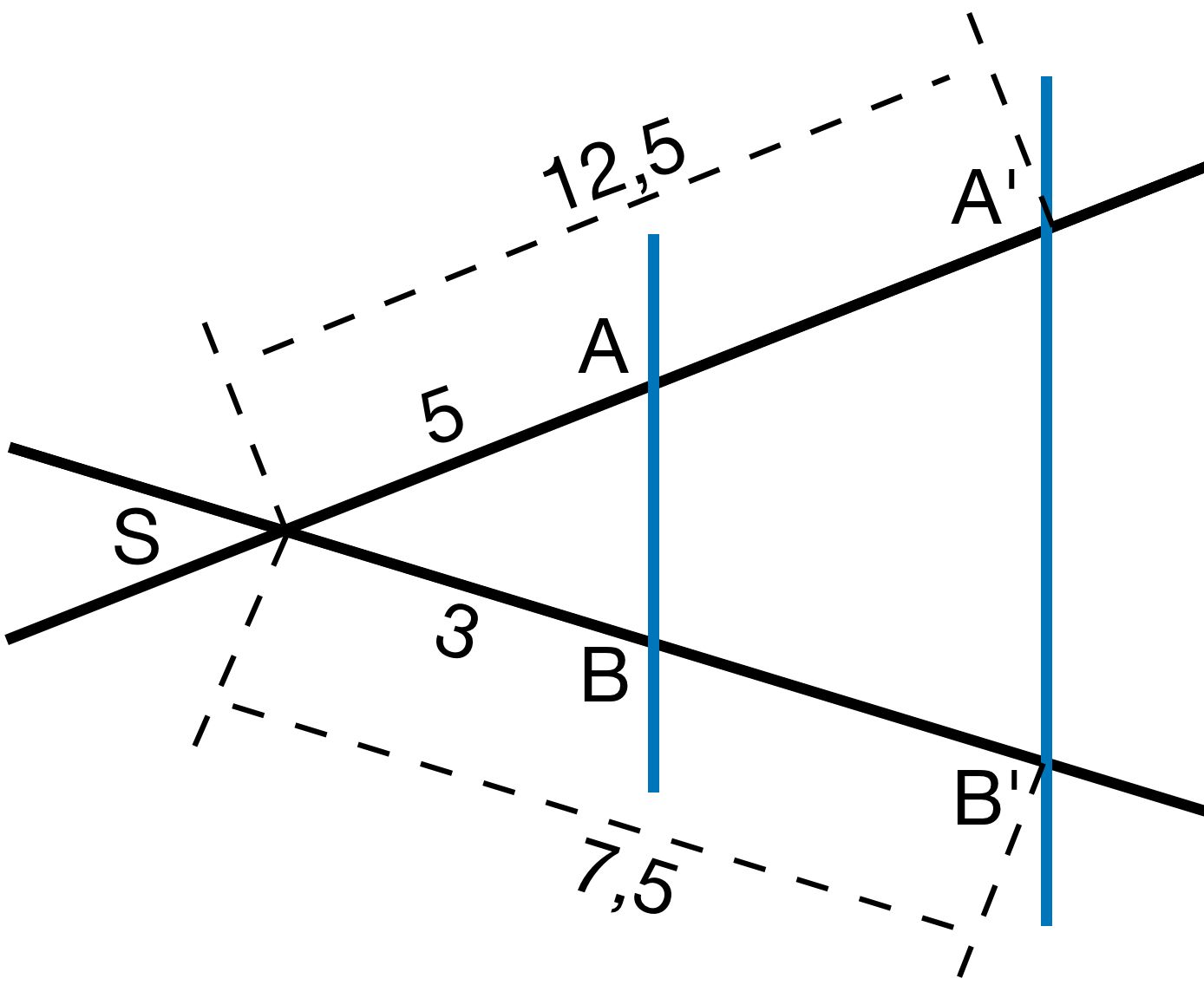
a)
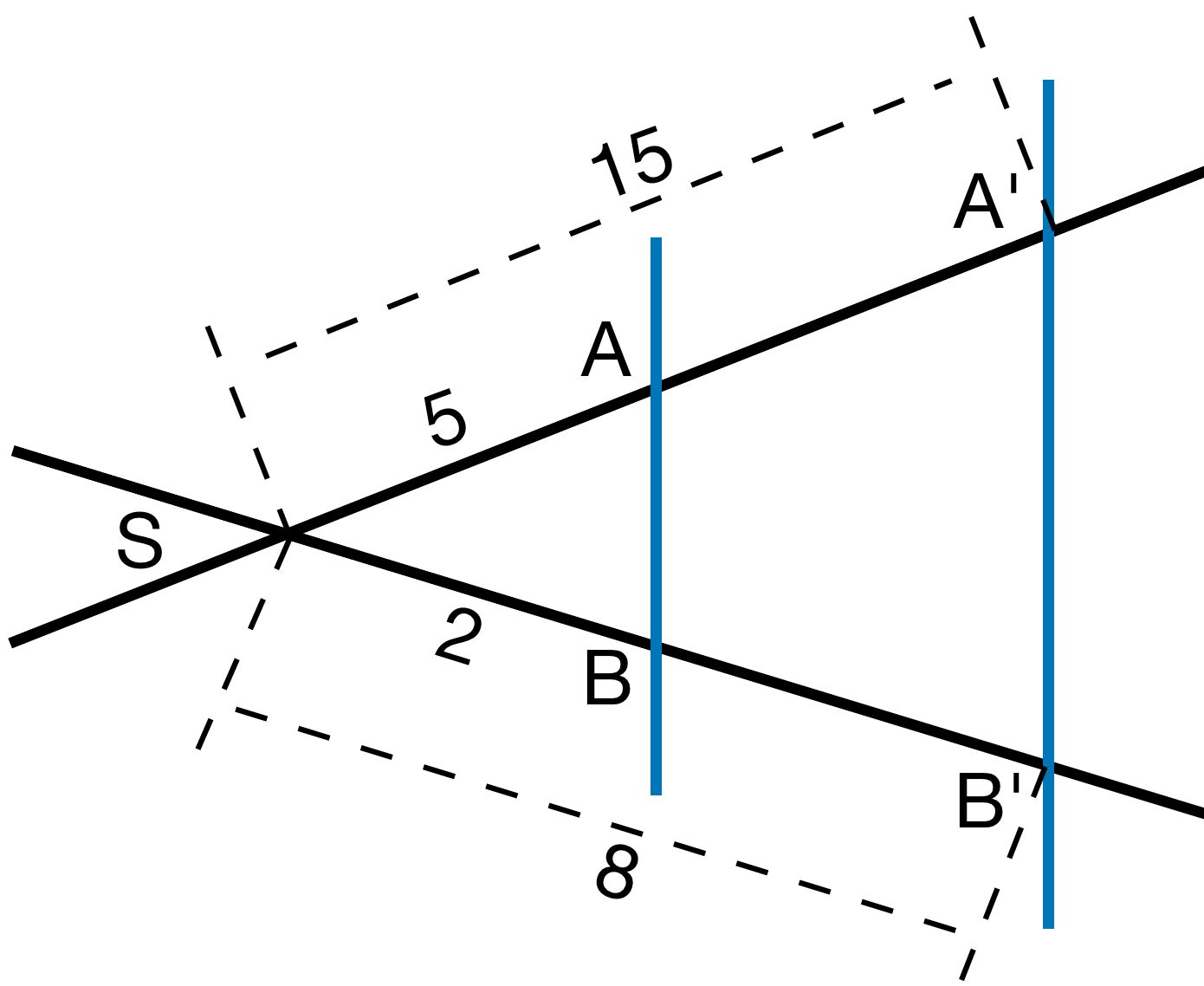
b)
Bereitgestellt von: Deliah Herbstritt Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/de0a5ca6
Seite: 2/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/de0a5ca6