HerunterladenAls PDF Herunterladen
  • Bruchteile von Gewichten
  • h.winterhalter
  • 16.05.2019
  • Mathematik
  • Bruchrechnen
  • R
  • 5
  • Einzelarbeit
  • Arbeitsblatt
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
Bruchteile von Gewichten
Mathematik Bruchrechnen R 5
1
Wie viel ist noch in der Packung? Wandle den Bruch in die gesuchte Einheit um.

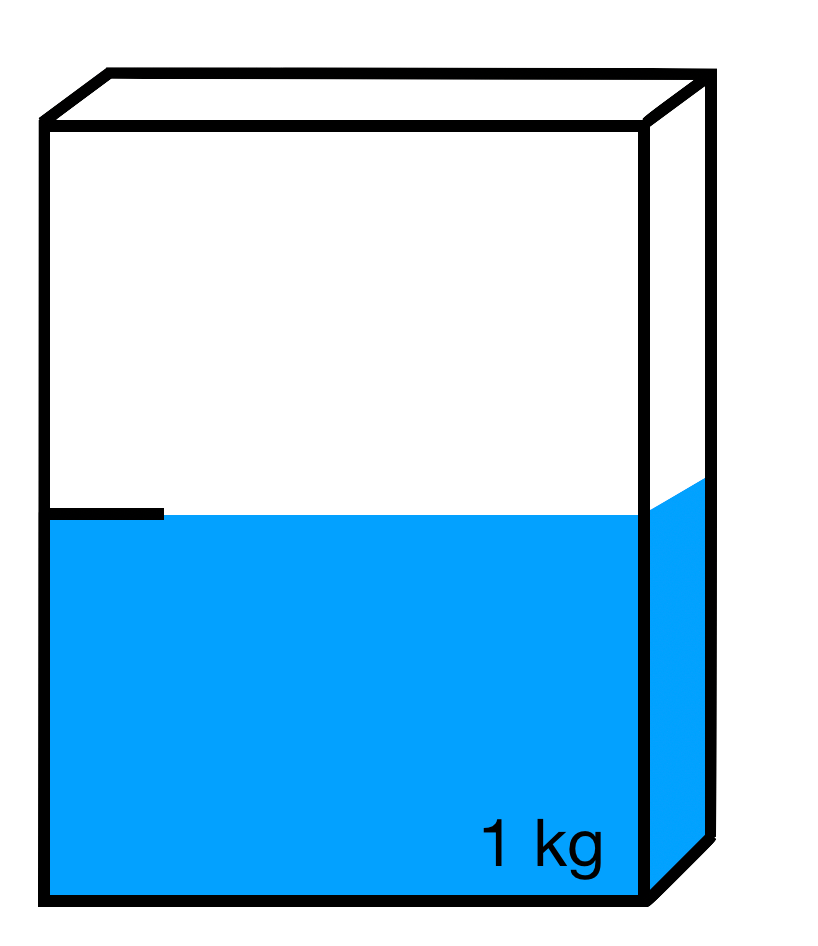
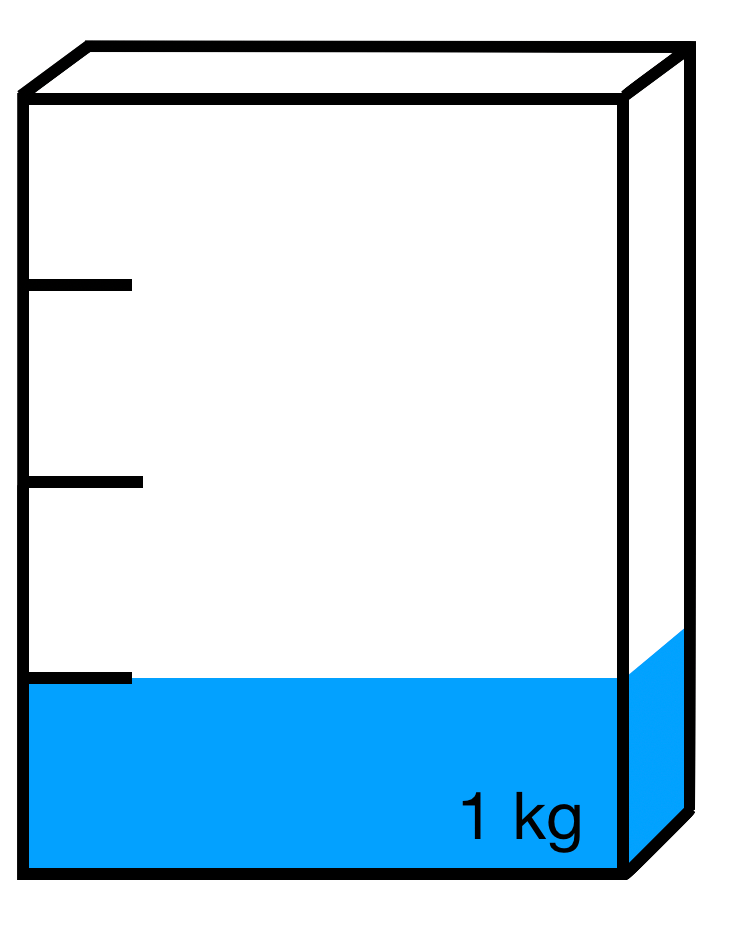
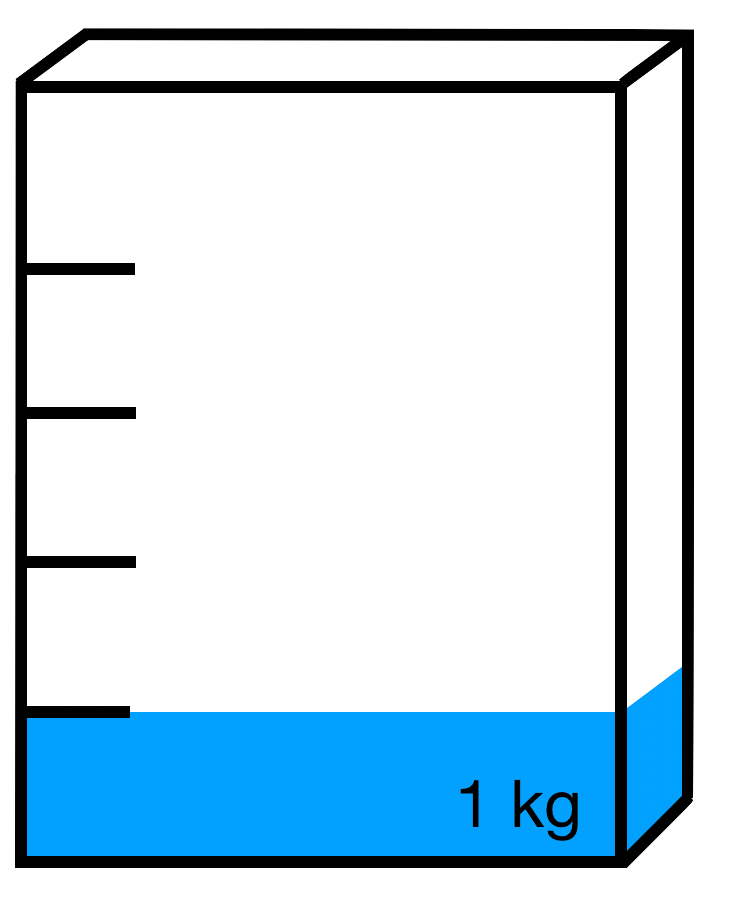
b)

c)

a)

14\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \cloze{\frac{1}{4}}

12\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \cloze{\frac{1}{2}}

15\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \cloze{\frac{1}{5}}

= g

= g

= g

kg

kg

kg

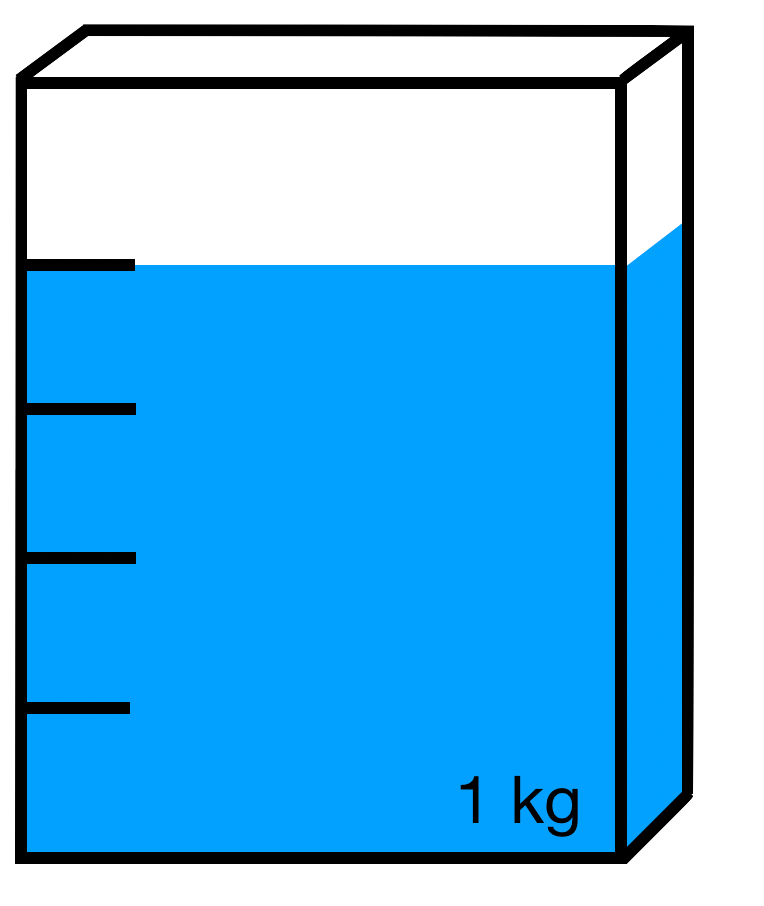
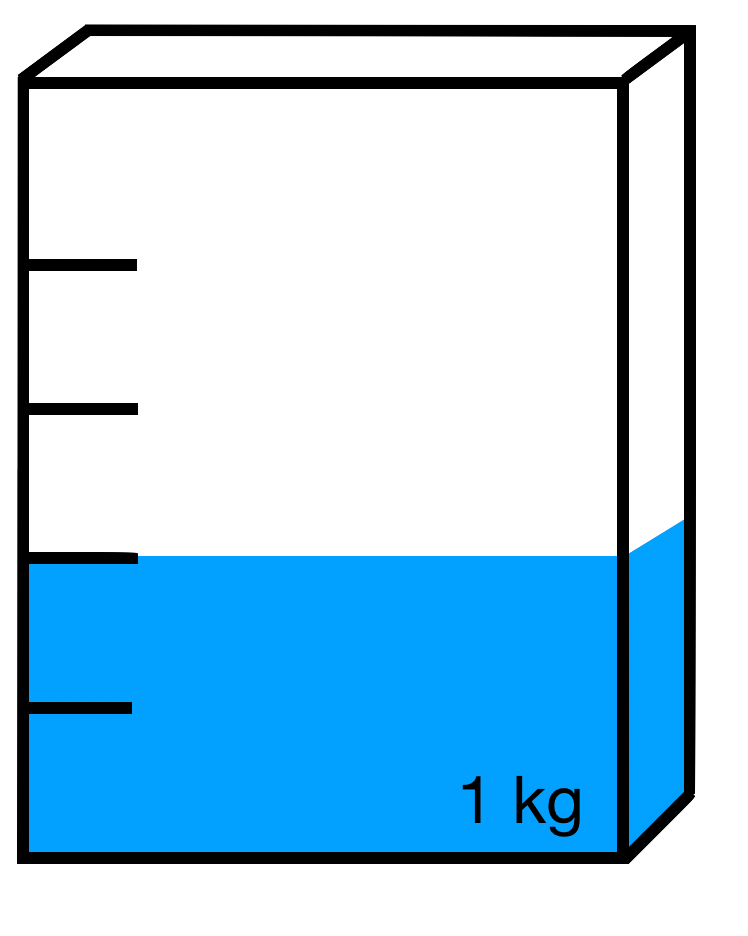
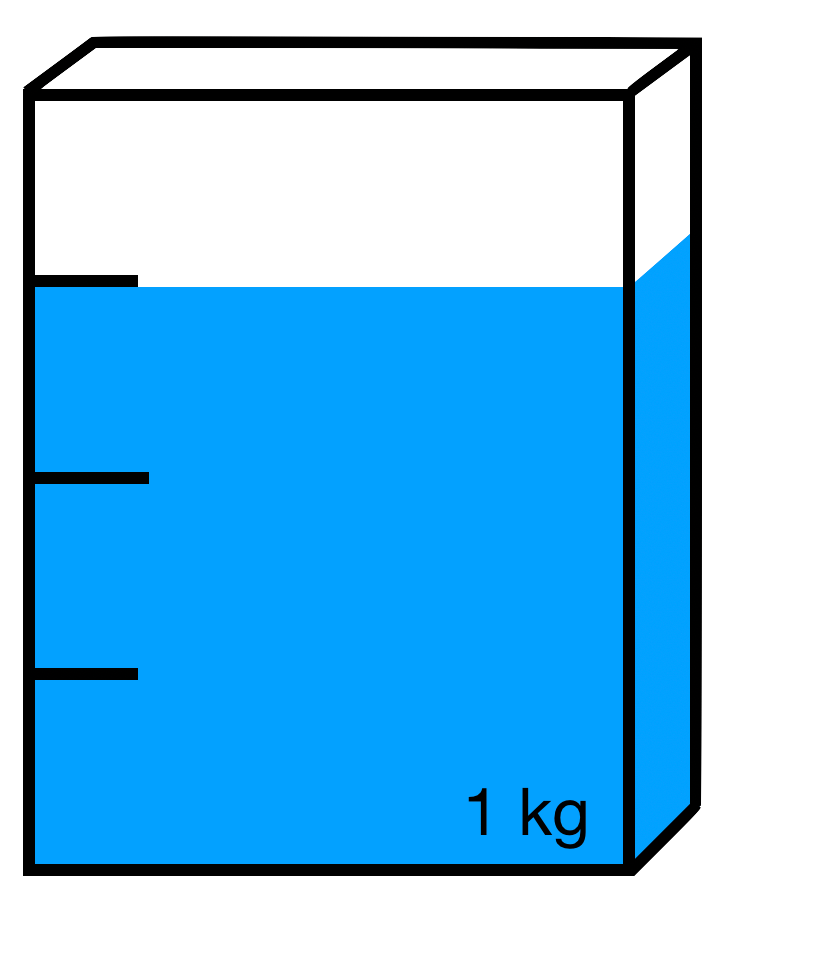
d)

e)

f)

25\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \cloze{\frac{2}{5}}

45\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \cloze{\frac{4}{5}}

34\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \cloze{\frac{3}{4}}

= g

= g

= g

kg

kg

kg

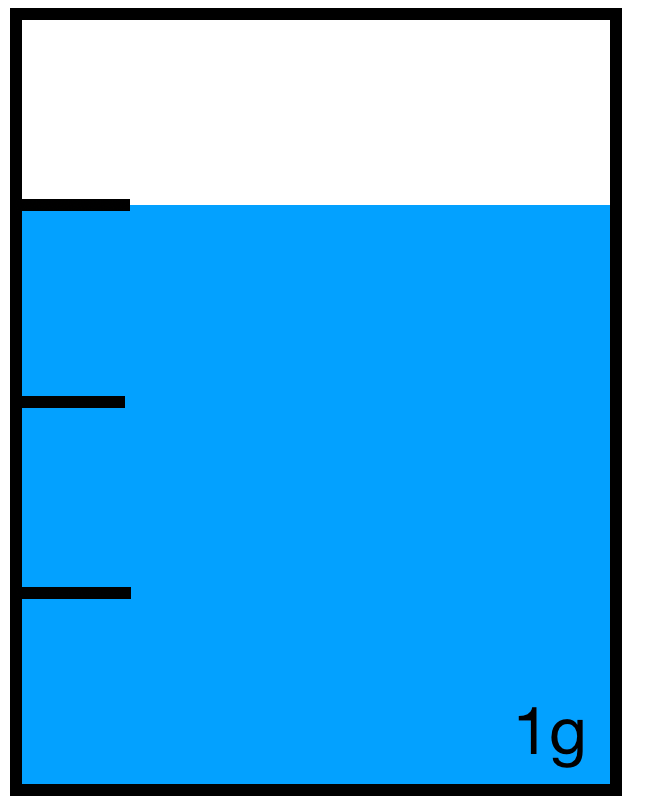
g)

h)

i)

12\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \cloze{\frac{1}{2}}

34\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \cloze{\frac{3}{4}}

14\gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \cloze{\frac{1}{4}}

= mg

= mg

= mg

g

g

g

Bereitgestellt von: h.winterhalter Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/dec5a539
Seite: 1/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/dec5a539
AB
Bruchteile von Gewichten
Mathematik Bruchrechnen R 5
2
Wie voll ist die Packung noch? Färbe die Grafik der Angabe entsprechend ein. Wie kann man die Angabe auch als Anteil darstellen?

a) \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 500 g

b) \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 250 g

kg

kg

c) \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 400 g

c) \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 750 g

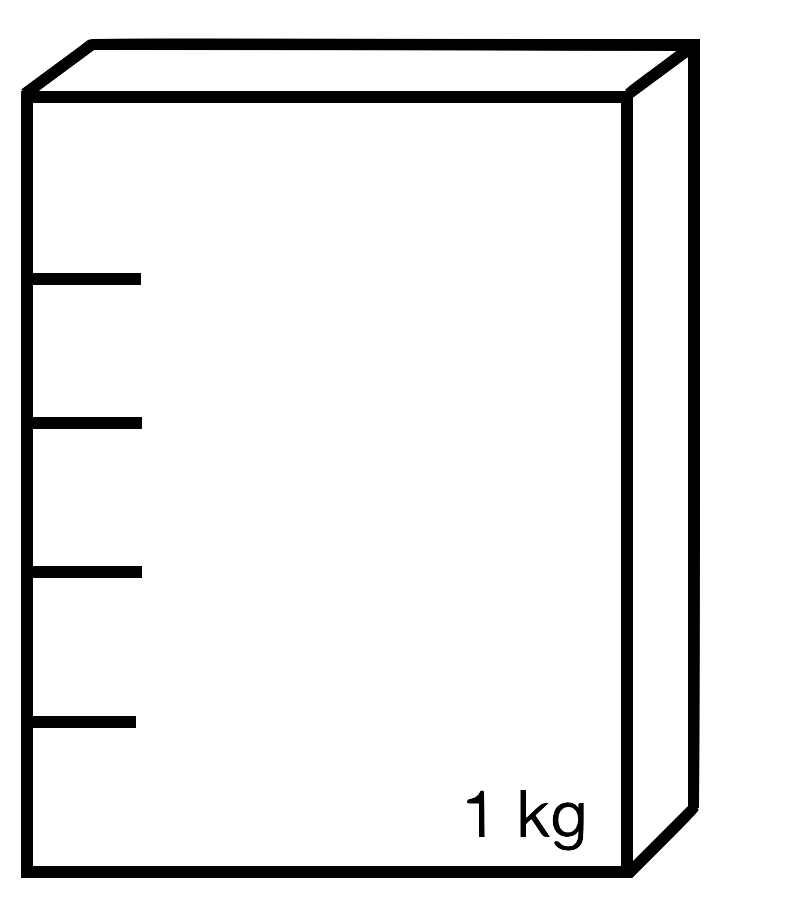
kg

kg

3
Wandle um!

a) \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 500 mg = g



c) \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 500 kg = t

b) \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 200 g = kg



d) \gdef\cloze#1{{\raisebox{-.05em}{\colorbox{none}{\color{transparent}{\large{$\displaystyle #1$}}}}}} \hspace*{0.26cm} 750 kg = t

Bereitgestellt von: h.winterhalter Stand: 21.07.2020 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/dec5a539
Seite: 2/2
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/dec5a539
x