Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
Übungen Pythagoras
Mathematik Flächen M 9
1
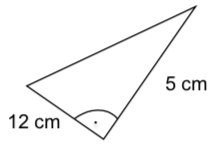
Berechne die die fehlende Länge des rechtwinkligen Dreiecks wie im Beispiel.
- a=13cmb=5cmc≈
Beispiel: gegeben: a=6cmb=3cmgesucht: c
a2+b2=c2
(6cm)2+(3cm)2=c2
36cm2+9cm2=c2
45cm2=c2∣
6,71cm≈c
b)

c)
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/e162a084
https://editor.mnweg.org/entdecken/dokument/e162a084
AB
Übungen Pythagoras
Mathematik Flächen M 9
2
Berechne die fehlende Länge des rechtwinkligen Dreiecks. Dafür musst du die Formel des Satz des Pythagoras umstellen wie im Beispiel.
- a=13cmb≈ c=10cm
Beispiel: gegeben: a=5cmc=9cmgesucht: b
c2−a2(9cm)2−(5cm)281cm2−25cm256cm2 67,48cm≈c=b2=b2=b2=b2∣
Hinweis
Die Variable c in der Formel steht für die Hypotenuse im Dreieck. Die Benennung in den Dreiecken kann jedoch nochmal anders sein.
b)
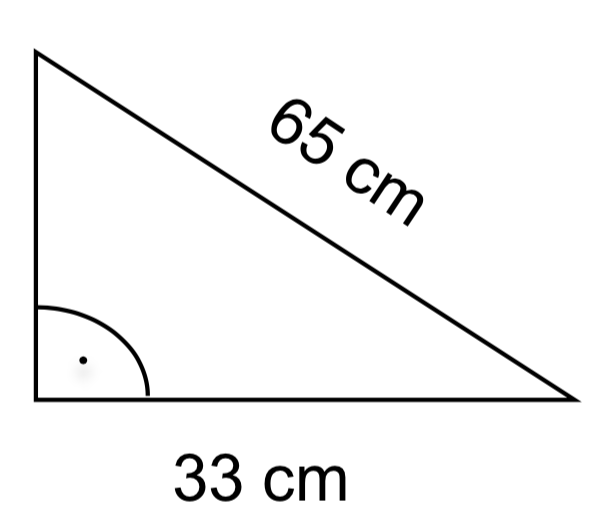
c)

Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/e162a084
https://editor.mnweg.org/entdecken/dokument/e162a084
AB
Übungen Pythagoras
Mathematik Flächen M 9
3
Berechne die Seitenlänge a, b und c des rechtwinkligen Dreiecks
a)a2ab)a2ac)a2ad)a2a=25cm2=25cm≈156,42cm2=156,42cm=81dm2≈81dm=202,98mm2=202,98mm
b2bb2bb2bb2b=25cm2=25cm=64cm2=64cm=391,71cm2=391,71cm=156mm2=156cm
c2cc2cc2cc2c=35,36cm2=156,42cm=169m2=169cm=400dm2=400dm=256mm2=256mm
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/e162a084
https://editor.mnweg.org/entdecken/dokument/e162a084


