Ist am An­fang eines Wachs­tums mehr als nur ein Mensch/Bak­te­ri­um/etc. vor­han­den, so er­wei­tert man die Ex­po­nen­ti­al­funk­ti­on zu $f(x)=B_0\cdot b^x$. (Man streckt die Funk­ti­on dabei um $B_0$ in y-​Richtung.) $B_0$ gibt den Stand am An­fang des Wachs­tums an.



Manch­mal wird die Ex­po­nen­ti­al­funk­ti­on $f(x)=B_0\cdot b^x$ auch als $N(t)=B_0\cdot b^t$ ge­schrie­ben. Das ist aber nur eine an­de­re Schreib­wei­se, bei der die Va­ri­a­ble t (statt x) ver­wen­det wird.



Ge­le­gent­lich ist der Pa­ra­me­ter b auch in Pro­zent an­ge­ge­ben. Hier musst du die Pro­zent­zahl in De­zi­mal­zah­len um­rech­nen.



Also ist ganz egal, wel­che Buch­sta­ben wir ver­wen­den. Wich­tig ist, dass x der Ex­po­nent ist.

Ver­su­che nun in den fol­gen­den Auf­ga­ben, ein paar der Ei­gen­schaf­ten der Ex­po­nen­ti­al­funk­ti­on selbst her­aus­zu­fin­den. Ent­schei­de je­weils, wel­che Ant­wor­ten rich­tig sind. Du kannst die Funk­ti­ons­glei­chung in dei­nen Ta­schen­rech­ner oder Geo­Ge­bra ein­ge­ben und dir an­zei­gen las­sen, um ver­schie­de­ne Funk­ti­o­nen aus­zu­pro­bie­ren.





Du hast viel­leicht fol­gen­de Ei­gen­schaf­ten von $B(t)=b^t$ $(b>0)$ her­aus­ge­fun­den:



• Die Ex­po­nen­ti­al­funk­ti­on hat nur po­si­ti­ve Funk­ti­ons­wer­te.

• Die Ex­po­nen­ti­al­funk­ti­on geht durch den Punkt (0|1).

• Die Ex­po­nen­ti­al­funk­ti­on nä­hert sich auf einer Seite der x-​Achse an. Die x-​Achse ist also eine Asym­pto­te.

• Die Ex­po­nen­ti­al­funk­ti­on ist bei Wachs­tum streng mo­no­ton stei­gend/wach­send und bei Zer­fall streng mo­no­ton fal­lend.





Pa­ra­me­ter b:

• für $b<1$: Zer­fall

• für $b=1$: $N(t)=1^t=1$ ⇒ keine Ex­po­nen­ti­al­funk­ti­on

• für $b>1$: Wachs­tum





Man nennt $b$ daher Wachs­tums- bzw. Zer­falls­fak­tor

Be­den­ke: Wie jede Funk­ti­on kann man auch die Ex­po­nen­ti­al­funk­ti­on $f(x)=b^x$

• ver­schie­ben

• stau­chen und stre­cken

• spie­geln



So kannst du z.B. mit dem Fak­tor B₀ die Funk­ti­on stau­chen bzw. spie­geln.

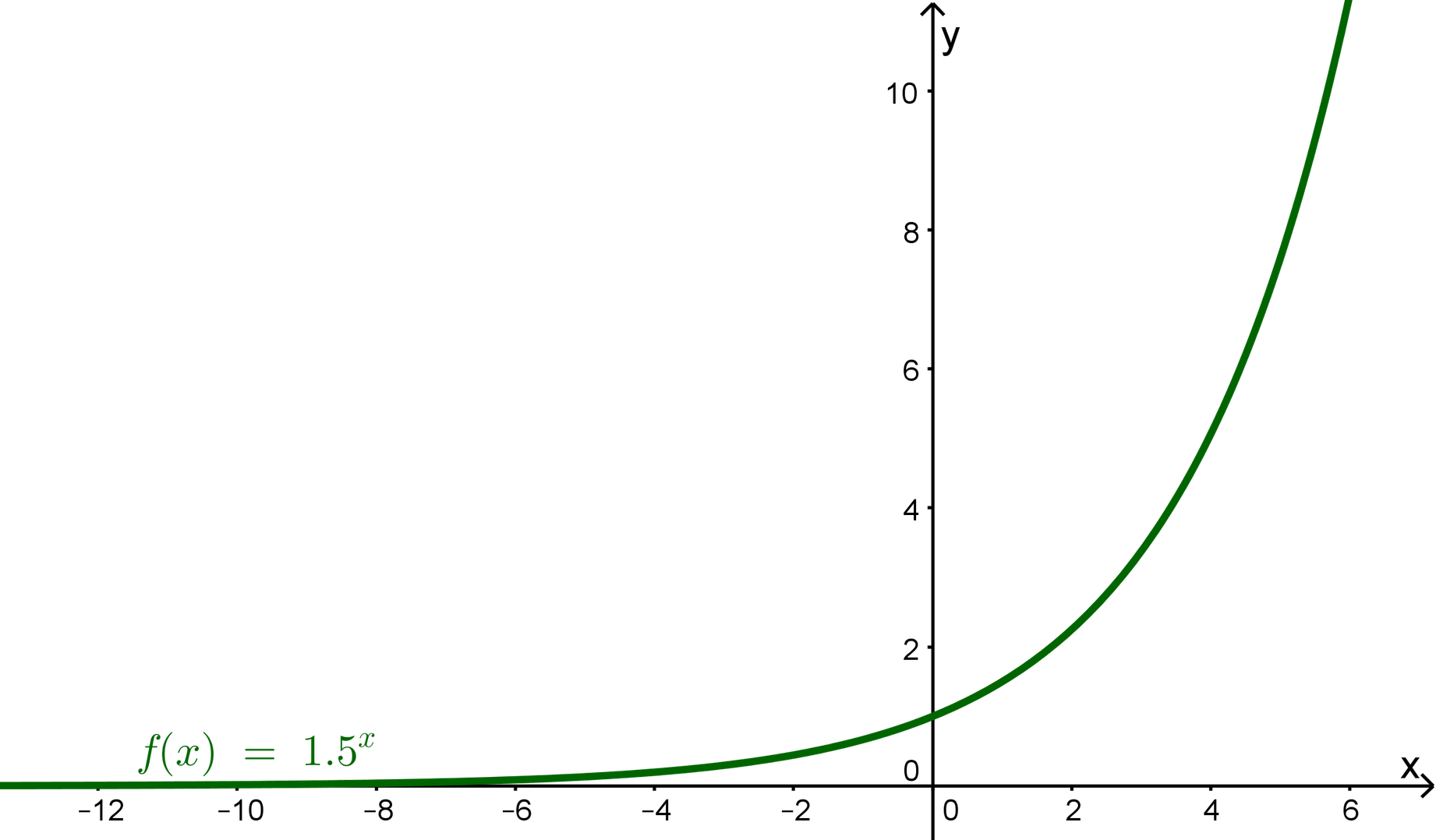
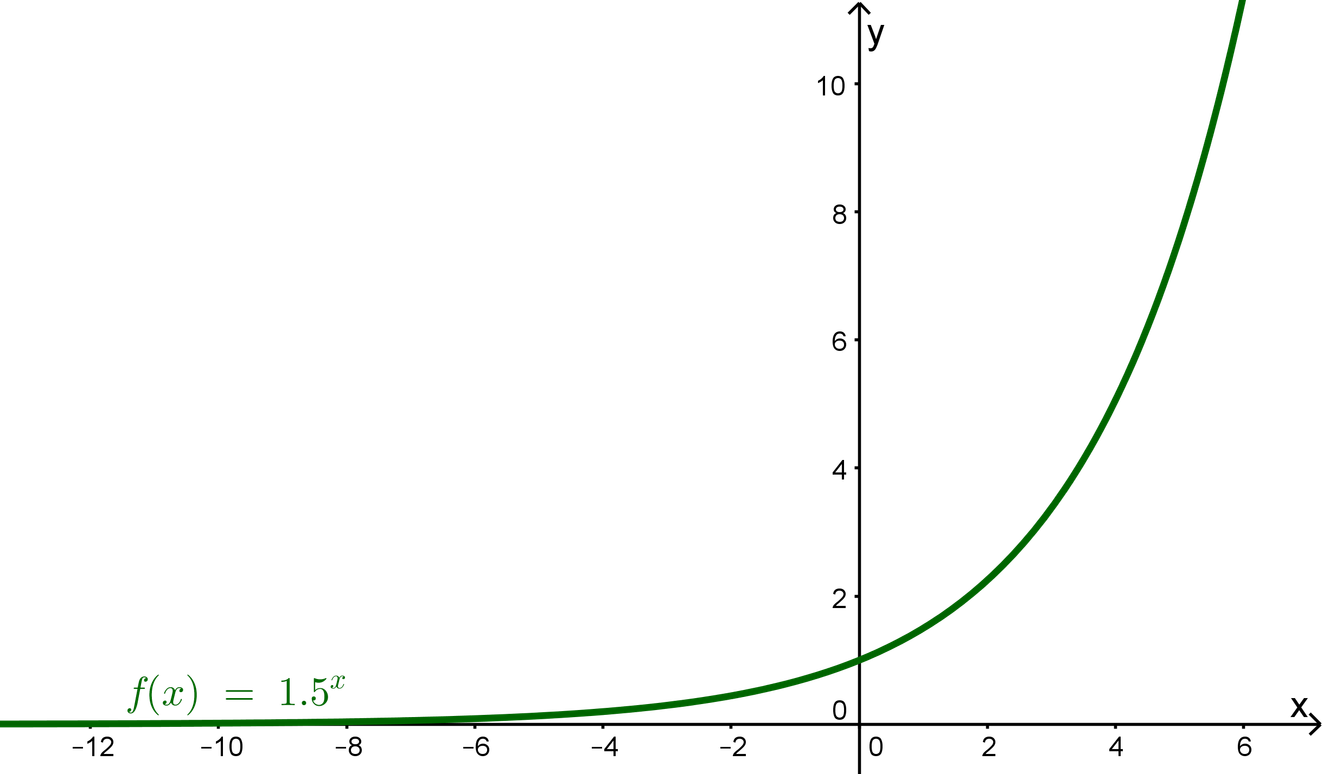
Bei­spiel für b = 1,5

Hin­weis: Glei­chun­gen, bei denen eine Va­ri­a­ble im Ex­po­nen­ten vor­kommt (z.B. $2^x=12$), kannst du rech­ne­risch noch nicht lösen. Hier­zu be­nö­tigst du den Log­arith­mus.