Was ist GeoGebra?
GeoGebra ist eine kostenlose dynamische Mathematiksoftware für SchülerInnen und LehrerInnen aller Altersstufen. Sie verbindet Geometrie, Algebra, Tabellen, Zeichnungen, Statistik und Analysis in einem einfach zu bedienenden Softwarepaket. GeoGebra hat außerdem eine stark wachsende Community mit Millionen von Nutzern aus fast allen Ländern der Welt. GeoGebra ist die weltweit führende Mathematiksoftware und unterstützt innovatives Lehren und Lernen in den Fächern Mathematik, Informatik, Naturwissenschaften und Technik rund um den Globus.
Das Programm wird ständig weiter entwickelt und erweitert. Das Programm sollte besser heruntergeladen (Windows/Mac/iOS) und installiert werden. Achte darauf, die GeoGebra Suite
herunterzuladen. Diese enthält alle Moduleinheiten. Das Programm ist kostenlos. Eine Registrierung ist nicht erforderlich, wird aber empfohlen, um Graphen zu speichern.
www.geogebra.org
https://editor.mnweg.org/entdecken/dokument/einfuehrung-geogebra-lnqxggrp
Hinweise zur Bedienung von GeoGebra
1. Dezimalzahlen werden mit einem Punkt abgetrennt
z.B. 0,5 -> 0.5 3,5 -> 3.5
2. Rechenzeichen in GeoGebra
Rechenzeichen
in GeoGebra
+
+
-
-
⋅
*
:
/
x5
x^5
8,1⋅108
8.1*10^8
3. Funktionsgraphen darstellen
Um den Graph einer Funktion darzustellen, gehen wir diese in der Befehlszeile ein und drücken auf Enter, z.B. f(x)=3x2+2
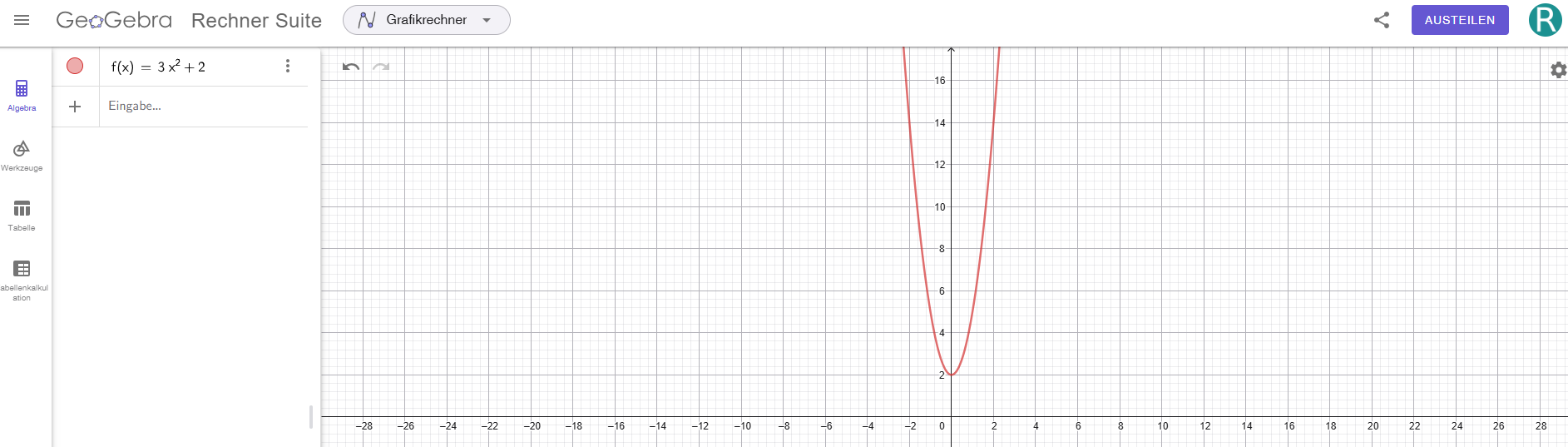
https://editor.mnweg.org/entdecken/dokument/einfuehrung-geogebra-lnqxggrp
Übersicht der Module
Modul 1
Inhalt:
Geführtes Kennenlernen des Programms Geogebra anhand quadratischer Funktionen.
Strecken, Stauchen, Verschieben der Parabel. Schnittpunkte von zwei Parabeln.
Voraussetzung:
Geogebra: Keine Voraussetzung.
Mathematisch: Quadratische Funktion in allgemeiner Form, Nullstellen, Schnittpunkte von Funktionen.
Modul 2
Inhalt:
Eigenständiges Erstellen einer dynamischen Graphik mit Schiebereglern: In allgemeiner Form und Scheitelpunktform. Strecken, Stauchen, Verschieben der Parabel. Nullstellen und Schnittpunkte von zwei Parabeln berechnen.
Voraussetzung:
Geogebra: Grundlagen mit Parametern, Schiebereglern und die Befehle: Nullstelle[f], Schneide[f,g]
Mathematisch: Quadratische Funktion in allgemeiner Form und Scheitelpunktform, Nullstellen, Schnittpunkte von Funktionen.
Modul 3
Inhalt:
Freie Aufgabenstellung. Eigenständiges Erstellen eines Bildes mit Parabelabschnitten.
Voraussetzung:
Geogebra: Grundlagen und der Befehl: Funktion[f,a,b]
Mathematisch: Quadratische Funktion in allgemeiner Form, Verschieben und Strecken/ Stauchen der Parabel.
https://editor.mnweg.org/entdecken/dokument/einfuehrung-geogebra-lnqxggrp


