Willkommen im Baustein Einführung negativer Zahlen

Nach diesem Baustein...

..... weißt du, was negative Zahlen sind und wo sie in der Umwelt zu finden sind.

..... kannst du negative und positive Zahlen ordnen und an der Zahlengerade ablesen.

..... kannst du Punkte im vollständigen Koordinatensystem eintragen und ablesen.

..... kennst du den Zusammenhang zwischen den Zahlenmengen.

Arbeitsschritte

Benötigte Arbeitsmittel

Step 1

Positive und negative Zahlen in der Umwelt

Step 2

Zahlen an der
Zahlengerade
ordnen

Step 3

Das vollständige Koordinatensystem

Step 4

Übersicht über die Zahlenbereiche

Fahrstuhl-Bastelbogen + Schnur
Arbeitsblatt Seite 1

Zahlengerade und Zahlenkärtchen laminiert
Arbeitsblätter Seite 2

Laptop für GeoGebra Applet
Arbeitsblatt Seite 3 und 4

Vorwissen

Baustein Brüche schon gelöst?

Um alle Aufgaben dieses Bausteins lösen zu können, solltest du die Bausteine Brüche I und Dezimalbrüche I bearbeitet haben.

Positive und negative Zahlen in der Umwelt

1

Sind dir schon einmal negative Zahlen, also Zahlen wie -2 oder -4, in deinem Alltag begegnet? Wenn ja, wo?
Tausche dich mit deinem Nachbarn aus und notiere drei Antworten in deinen Hefter!

2

Bastle mit Hilfe der Vorlage und dem Faden das Haus mit Fahrstuhl zusammen. Bring Leben in das Haus und trage die restlichen Zahlen in die Etagen unter- und oberhalb der 0 ein. Nutze dabei die negativen Zahlen. Vervollständige, wenn du möchtest, das Haus mit weiteren Gegenständen und Lebewesen.

Fahrstuhlaufgaben

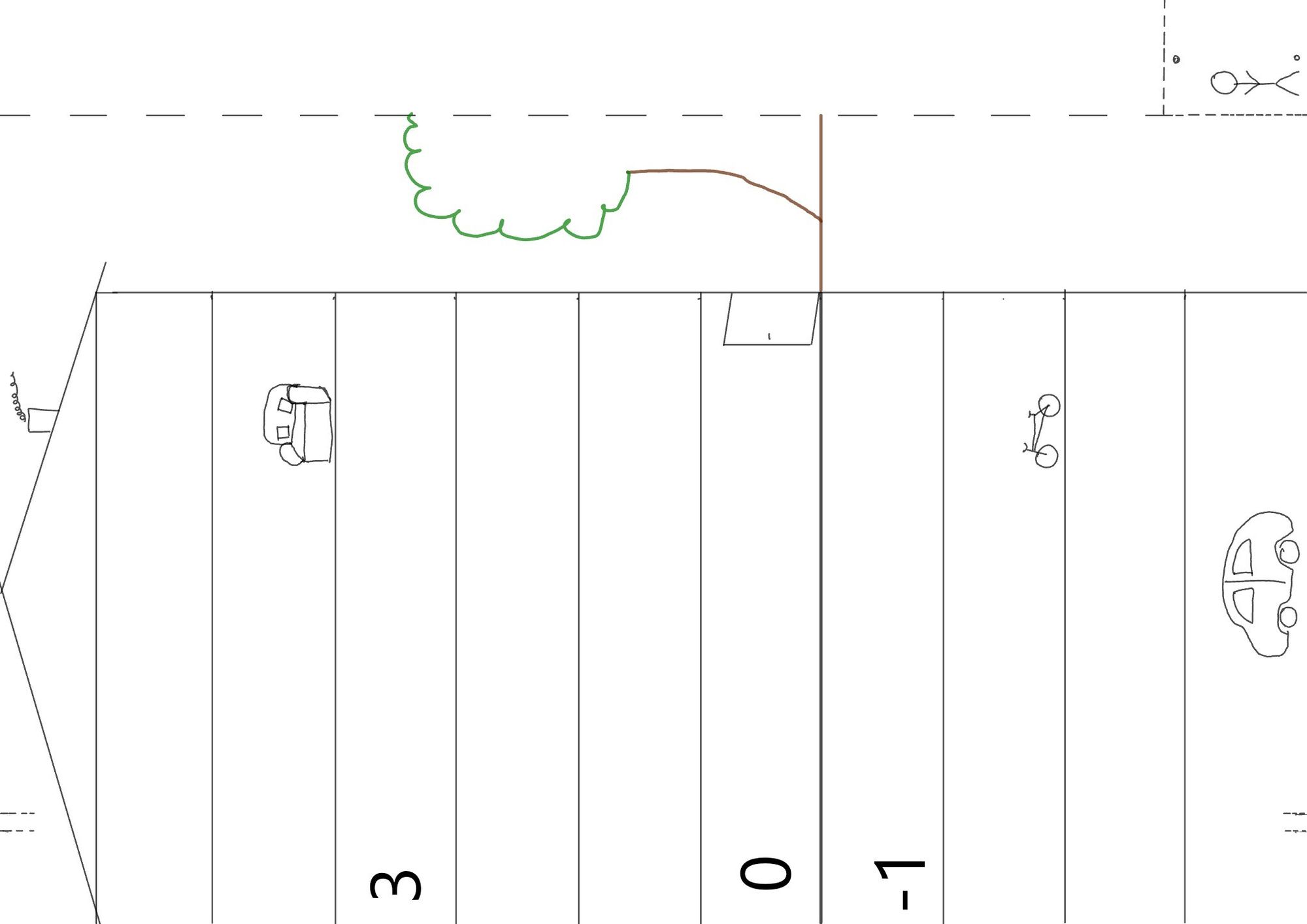
Nutze für die folgenden Aufgaben deinen selbst gebastelten Fahrstuhl zur Unterstützung.

3

In welchem Stockwerk steigen die Personen aus?
Notiere die Etagen in deinem Hefter und überprüfe deine Ergebnisse mit
deinem selbst gebastelten Fahrstuhl.

Frau Müller fährt von Stockwerk 4 drei Stockwerke abwärts.
Herr Schneider fährt von Stockwerk -2 zwei Stockwerke abwärts.
Fatime fährt von Stockwerk 2 vier Stockwerke abwärts.
Thomas fährt von Stockwerk -2 fünf Stockwerke aufwärts.
Herr Gül ist in Stockwerk -3 und will ins Stockwerk -1. Wie viele Stockwerke muss er fahren?
Tonio ist in Stockwerk -2 und möchte ins Stockwerk 4. Wie viele Stockwerke muss er fahren?

4

Übernimm die Tabelle in deinen Hefter und ergänze die fehlenden Angaben für die Fahrstuhlfahrten. Plus-Zeichen bei der Fahrt bedeuten Fahrstuhlfahrten nach oben, Minus-Zeichen Fahrten nach unten.

Einstieg

- 1

0

- 2

- 4

Fahrt

- 3

+ 4

+ 5

- 3

+ 4

Ausstieg

- 4

- 2

2

0

Rechnung

-1-3 = -4

0+4=4

2-4=-2

5

Übernimm den Merksatz in deinen Hefter.

Merksatz: negative Zahlen

Negative Zahlen sind Zahlen, die kleiner als 0 sind.

So zum Beispiel: -1; -2; - 500; - 5,7; - 3,8, $- \frac{1}{4}; - \frac{7}{8}$ .

Mit den negativen Zahlen sind Aufgaben wie 3 - 5 = - 2 lösbar.

Das Minus der negativen Zahlen wird Vorzeichen genannt.

6

Unter oder über der Wasseroberfläche? Auch hier begegnen uns negative Zahlen im Alltag. Trage in deinem Hefter ein, in welcher Höhe die Gegenstände liegen und wo der Fisch schwimmt.

Beispiel
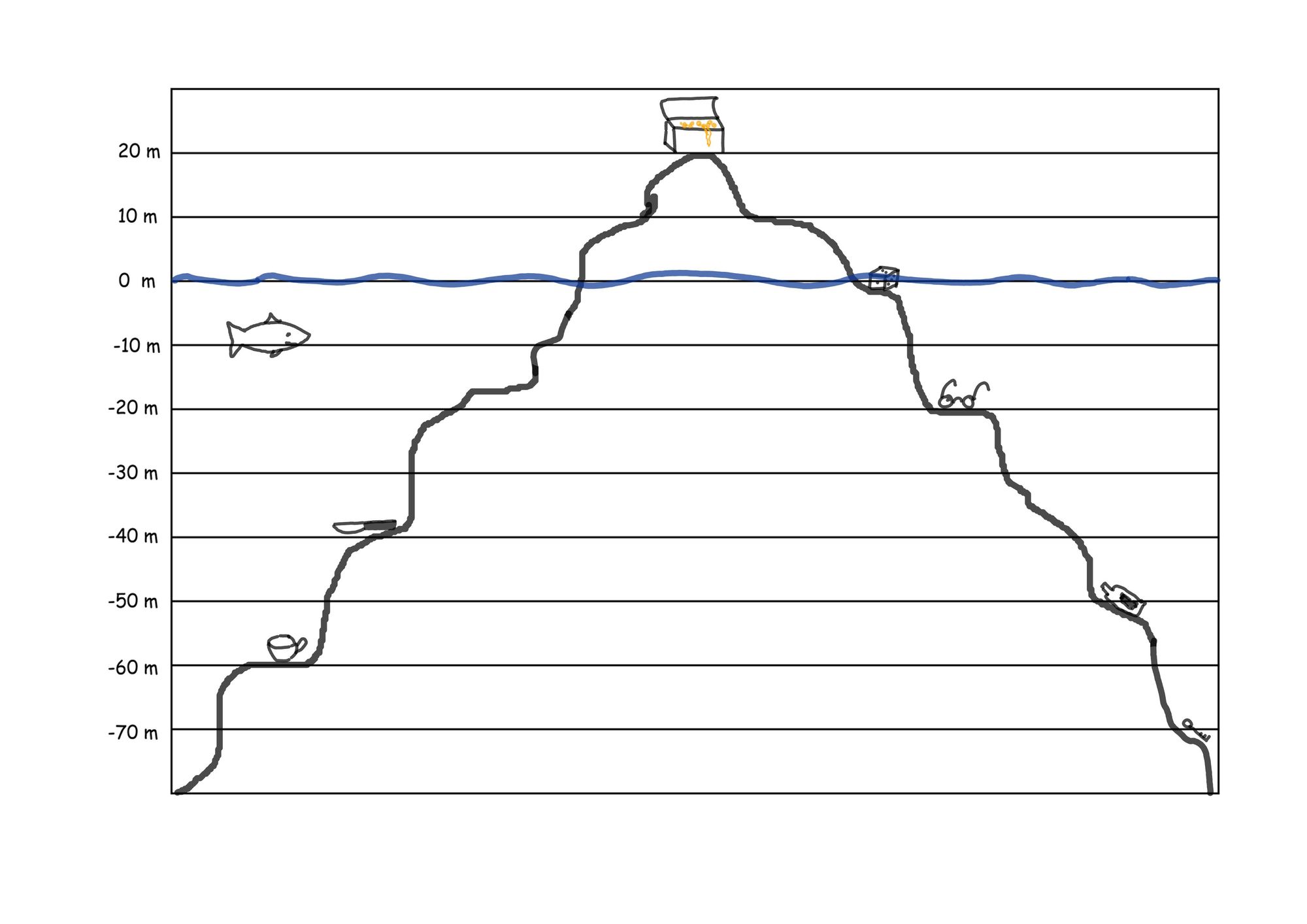
Brille: -20 m

Die Aufgabe 7 findest du auf dem kopierten Arbeitsblatt. Danach geht es hier weiter.

Relationszeichen

< kleiner als

> größer als

= gleich

8

Ordne die abgelesenen Temperaturen aus Aufgabe 7.
Beginne mit der niedrigsten Temperatur und setze das richtige Relationszeichen. Schreibe deine Lösung in deinen Hefter.

- 10°C < - 8°C < ...

Die Zahlengerade

Du weißt nun, was negative Zahlen sind. Jetzt erweitern wir den Zahlenstrahl zur Zahlengerade.

Du kannst dir vorstellen, die Zahlengerade sei die Skala eines (liegenden) Thermometers: Je niedriger die Temperatur, desto kleiner die Zahl.

Die Zahlen, die kleiner als 0 sind, stehen links von der 0 und erhalten als Vorzeichen ein - (Minus). Sie heißen negative Zahlen.

Die Zahlen, die größer als 0 sind, heißen positive Zahlen. Das Vorzeichen ist +. Es wird meistens nicht geschrieben.

Die Zahlengerade ist spiegelbildlich zur 0 aufgebaut. Deshalb hat z.B. die Zahl -3 den gleichen Abstand zur 0 wie die Zahl 3.

9

Übertrage die Überschrift, die Zahlengerade und den Merksatz in deinen Hefter!
Der Abstand zwischen den Zahlen auf deiner Zahlengerade soll jeweils 1cm betragen.

Merksatz:

Die Zahlengerade ist spiegelbildlich zur 0 aufgebaut.

Die Zahlen die kleiner als 0 sind, erhalten als Vorzeichen ein - (Minus).

Sie heißen negative Zahlen.

Die Zahlen auf der Zahlengerade werden von links nach rechts immer größer und

von rechts nach links immer kleiner.

10

Bewegungsaufgabe zur Zahlengerade auf dem Boden (laminierte Zahlengerade, Partnerarbeit)

Wählt einen unter euch, der die Teilaufgaben (a bis e) vorliest. Der Partner oder die Partnerin positioniert sich an der entsprechenden Zahl auf der Zahlengeraden. Startzahl ist die 0

Gehe 5 Zahlen in Minusrichtung.
Bei welcher Zahl stehst Du? Welcher Rechenaufgabe entspricht das?
Welche Zahl ist kleiner bzw. größer? (Startzahl oder Zielzahl?)
Gehe nun 3 Zahlen in Plusrichtung.
Bei welcher Zahl stehst Du?
Wie heißt die dazugehörige Rechenaufgabe?
Welche Zahl ist die kleinere bzw. die größere? Begründe!
Stelle die Rechenaufgabe -3 + 4 = ... dar und bestimme das Ergebnis!
Vergleiche Start- und Zielzahl nach der Größe.

Stelle eine Rechenaufgabe auf der Zahlengerade dar. Lass jemand anderen raten, welche Aufgabe du meinst.
Denkt euch (mindestens drei) weitere Teilaufgaben aus, die so ähnlich wie Teilaufgabe c) und d) sind.
Tauscht nun die Rollen!
Wiederholt die Teilaufgaben c), d) und e).

11

Um diese Aufgabe lösen zu können, musst du die Bausteine Brüche I und Dezimalbrüche I bereits bearbeitet haben.
Du kannst diese Aufgabe aber auch erst einmal überspringen.

Lege die Kärtchen mit den verschiedenen positiven und negativen Brüchen an den richtigen Stellen an der Zahlengerade an.
(Kontrolle mit Lösungsblatt.)

Bearbeite nun die Seiten 2 und 3 des kopierten Arbeitsblattes.

Dort findest du die Aufgaben 12 bis 16. Danach geht es hier weiter.

Viel Erfolg!

Das vollständige Koordinatensystem

Verlängern wir nun die x-Achse und die y-Achse über den Punkt (0; 0) hinaus nach links bzw. nach unten, so erhalten wir ein vollständiges Koordinatensystem.

Es besteht aus zwei Zahlengeraden, der x-Achse und der y-Achse, die sich senkrecht im Koordinatenursprung (0; 0) schneiden.

Man teilt das Koordinatensystem in vier Quadranten. Die Nummerierung ist entgegen dem Uhrzeigersinn.

(Der Punkt A hat die

x-Koordinate -4 und die y-Koordinate 2.

Der Punkt B hat die

x-Koordinate 4 und die y-Koordinate -2.)

2. Quadrant

1. Quadrant

3. Quadrant

4. Quadrant

18

Gehe über diesen Link oder den QR-Code zum interaktiven Arbeitsblatt in GeoGebra:

https://www.geogebra.org/m/vhu6cweq

Viel Spaß beim Bearbeiten!

Übersicht über die Zahlenbereiche - Die rationalen Zahlen ℚ

Natürliche Zahlen (Symbol $N$ ) stehen für Anzahlen (also 0, 1, 2, 3, 4, usw.).

Brüche (Symbol $Q +$ ) erhältst du als Ergebnis der Division zweier natürlicher Zahlen,

wie z.B. 3 : 4 = $\frac{3}{4}$ oder 1 : 3 = $\frac{1}{3}$ . Auch endliche und periodische Dezimalzahlen gehören dazu,

wie z.B. $0, 25 = \frac{1}{4}$ oder $0, \overset{ˉ}{6} = 0, 66666... = \frac{2}{3}$ .

Ganze Zahlen $(Z)$

Nimmst Du zu den natürlichen Zahlen jeweils die negativen Gegenzahlen dazu:

also zur 1 die -1 und zur 2 die -2 usw., dann erhältst du die ganzen Zahlen (Symbol $Z$ ).

Rationale Zahlen $(Q)$

Nimmst Du zu den Brüchen jeweils die negativen Gegenzahlen dazu,

also zur $\frac{3}{4}$ die $- \frac{3}{4}$ und zur $\frac{1}{3}$ die $- \frac{1}{3}$ , so erhältst du die rationalen Zahlen (Symbol $Q$ ).

Auch die ganzen Zahlen $Z$ gehören zur Menge der rationalen Zahlen $(Q)$ .

Diagramm

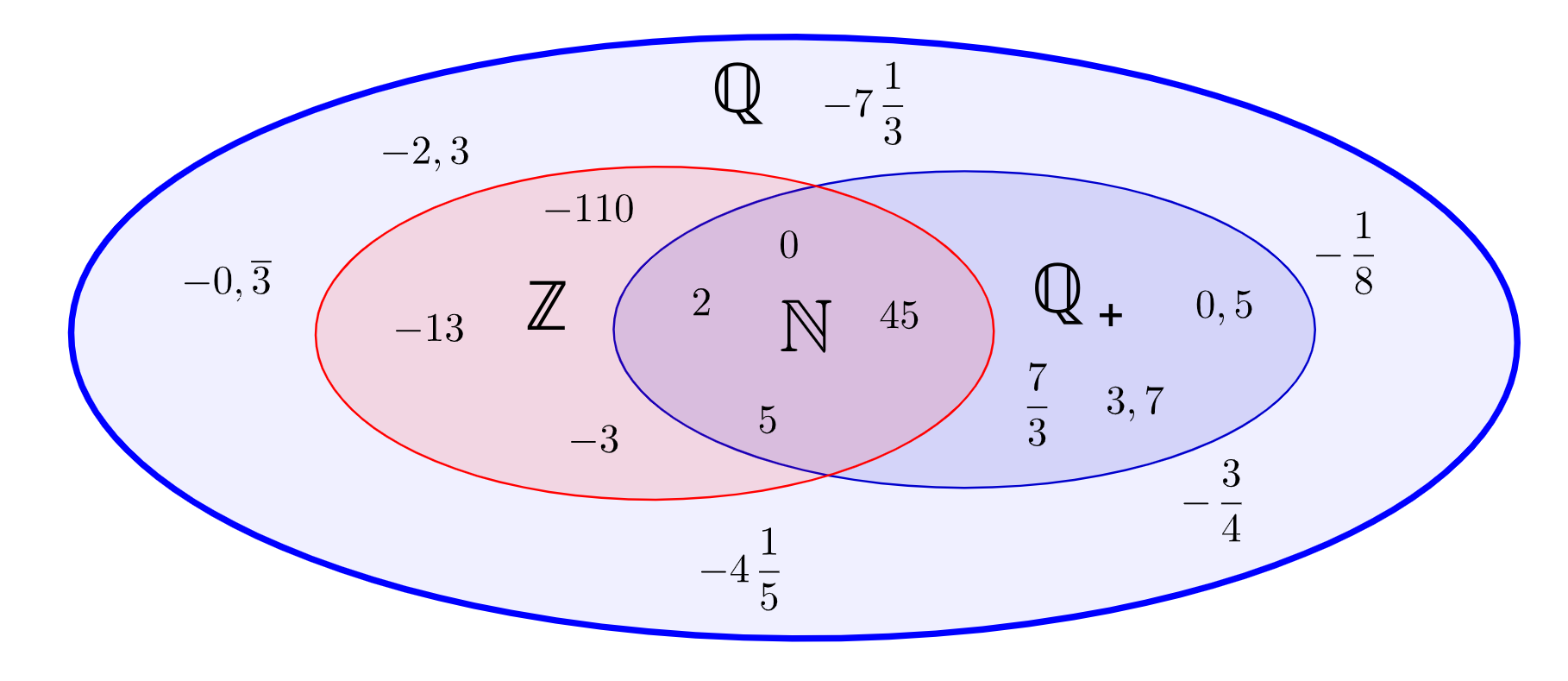
In diesem Diagramm sind die Zusammenhänge zwischen den verschiedenen Zahlbereichen dargestellt:

Die kleinste Menge ist die Menge der natürlichen Zahlen ℕ.

Sie sind ein Teil der ganzen Zahlen ℤ und auch ein Teil der Brüche ℚ+.

Die ganzen Zahlen ℤ, zusammen mit den negativen und den positiven Brüchen sind die Menge der rationalen Zahlen ℚ.

21

Übernimm das Diagramm in deinen Hefter.
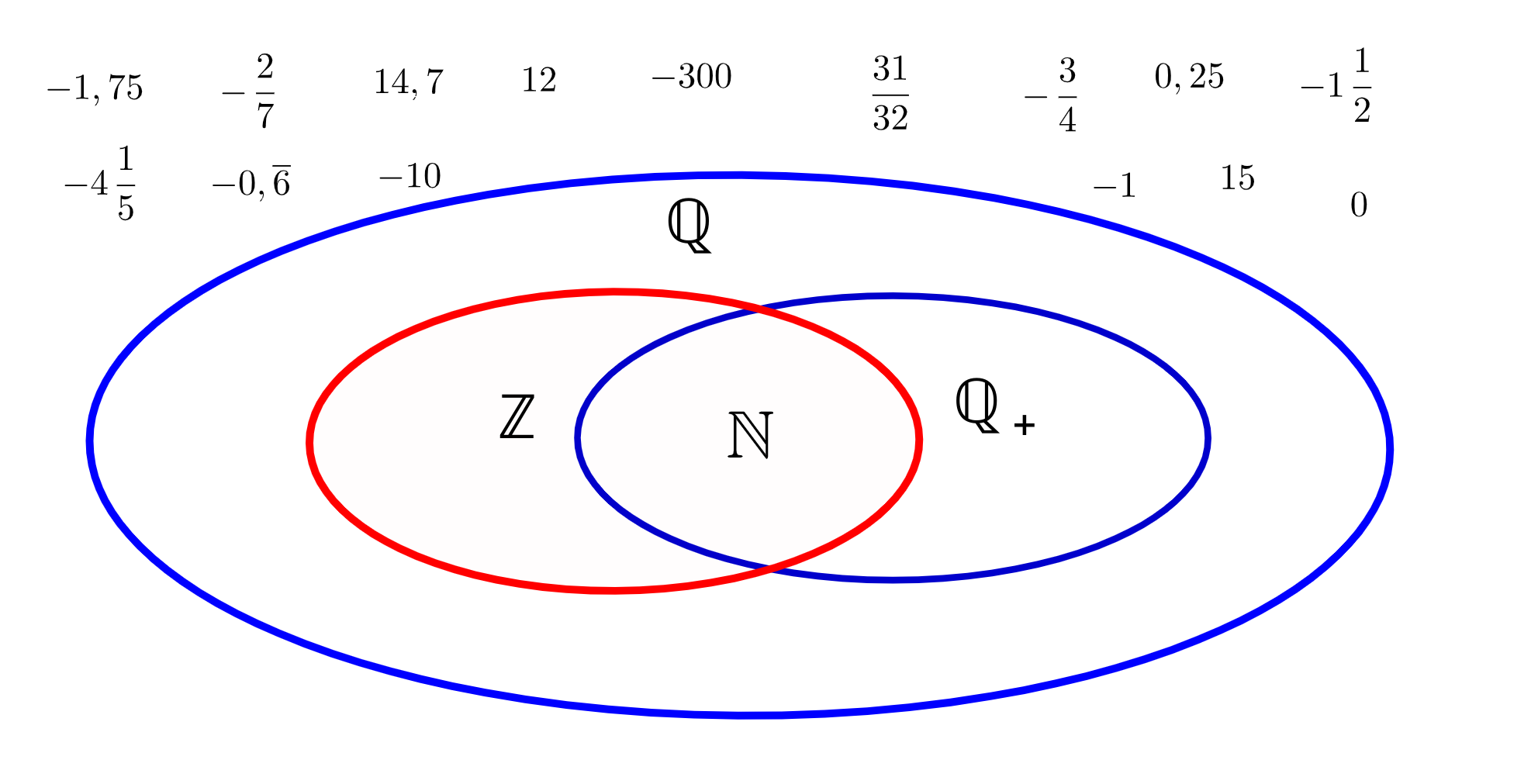
Trage die daneben stehenden Zahlen in den jeweils kleinsten Zahlenbereich ein.
Vergleiche mit dem Lösungsblatt.

Diagramm

22

Übernimm die Tabelle in deinen Hefter und kreuze wie im Beispiel alle richtigen Aussagen an.

Zahl

$- 23$

$0, 3$

$- 22, 5$

$- 3 \frac{1}{3}$

$\frac{3}{5}$

$57$

$\frac{1}{4}$

- $\frac{1}{4}$

0

$- 8$

ℕ

ℤ

x

ℚ+

ℚ

x