Quadratische Funktionen erkunden
Im Alltag kannst du immer wieder bogenförmige Bauwerke und Brücken entdecken, weil sich diese Form über die Jahrhunderte hinweg als besonders günstig erwiesen hat (und es zudem auch noch hübsch aussieht).
Auch in der Natur fallen solche Bögen immer wieder auf, zum Beispiel bei Bergmassiven.






https://editor.mnweg.org/entdecken/dokument/einstieg-quadratische-funktionen
Selbst beim Besuch eines Basketball- oder Fußballspiels ist es möglich vergleichbare Bögen zu entdecken. Achte einmal darauf, wie ein abgeworfener oder abgeschossener Ball durch die Luft fliegt.

Probiere es selbst einmal aus, indem du für einen Basketballwurf vorhersagst, ob der Ball im Korb landet oder nicht:
https://editor.mnweg.org/entdecken/dokument/einstieg-quadratische-funktionen
Quadratische Funktionen - Was genau bedeutet das überhaupt?
Die Worte für sich kannst du schon einordnen. Ein Quadrat ist eine geometrische Figur bei der alle Seiten gleich lang sind. Was Funktionen sind, konntest du auf den letzten Seiten dieses Lernpfades ausführlich wiederholen.
Schauen wir uns doch einmal an, ob wir eine Verbindung zwischen Quadraten und Funktionen herstellen können, die uns schließlich zu quadratischen Funktionen führt.
Dazu zeichnen wir ein Quadrat mit der Seitenlänge 1 cm und berechnen dessen Flächeninhalt:
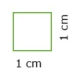
Dasselbe können wir nun mit Quadraten der Seitenlängen 2 cm, 3 cm und 4 cm machen und die Werte in einer Tabelle zusammenfassen:
Seitenlänge
1 cm
2 cm
3 cm
4 cm
5 cm
Fläche
1cm2
4cm2
9cm2
16cm2
25cm2
Für ein beliebiges Quadrat kann man die Seitenlänge mit x bezeichnen. Mit der Formel für den Flächeninhalt des Quadrates ergibt sich dann A = x2. Den Flächeninhalt kannst du als Funktion von x ansehen und f(x)=x2oder y=x2schreiben.
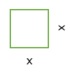
Seitenlänge = x
1 cm
2 cm
3 cm
4 cm
5 cm
Fläche =y=x2
1cm2
4cm2
9cm2
16cm2
25cm2
https://editor.mnweg.org/entdecken/dokument/einstieg-quadratische-funktionen
Wie sieht der Graph über den Flächeninhalt eines Quadrates mit der Seitenlänge x aus?
Zeichne den Graph der Funktion in das gegebene Koordinatensystem ein. Die Lösung findest du auf der nächsten Seite.
https://editor.mnweg.org/entdecken/dokument/einstieg-quadratische-funktionen
Lösung:
Als Graph erhältst du die Normalparabel der Funktion y=x2
Der Term y=x2 bzw. f(x)=x2 beschreibt die einfachste quadratische Funktion.
Den Graphen dieser quadratischen Funktion nennt man Normalparabel.
Die Normalparabel hat ihren tiefsten Punkt an der Stelle S(0|0). Dieser Punkt wird Scheitelpunkt genannt.
https://editor.mnweg.org/entdecken/dokument/einstieg-quadratische-funktionen


