Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
AB
1. Strahlensatz umstellen
Mathematik Flächen R 9
1
Berechne die fehlende Seitenlänge X. Die Maßeinheit ist cm. Runde wenn nötig auf zwei Stellen nach dem Komma.
Beispiel:
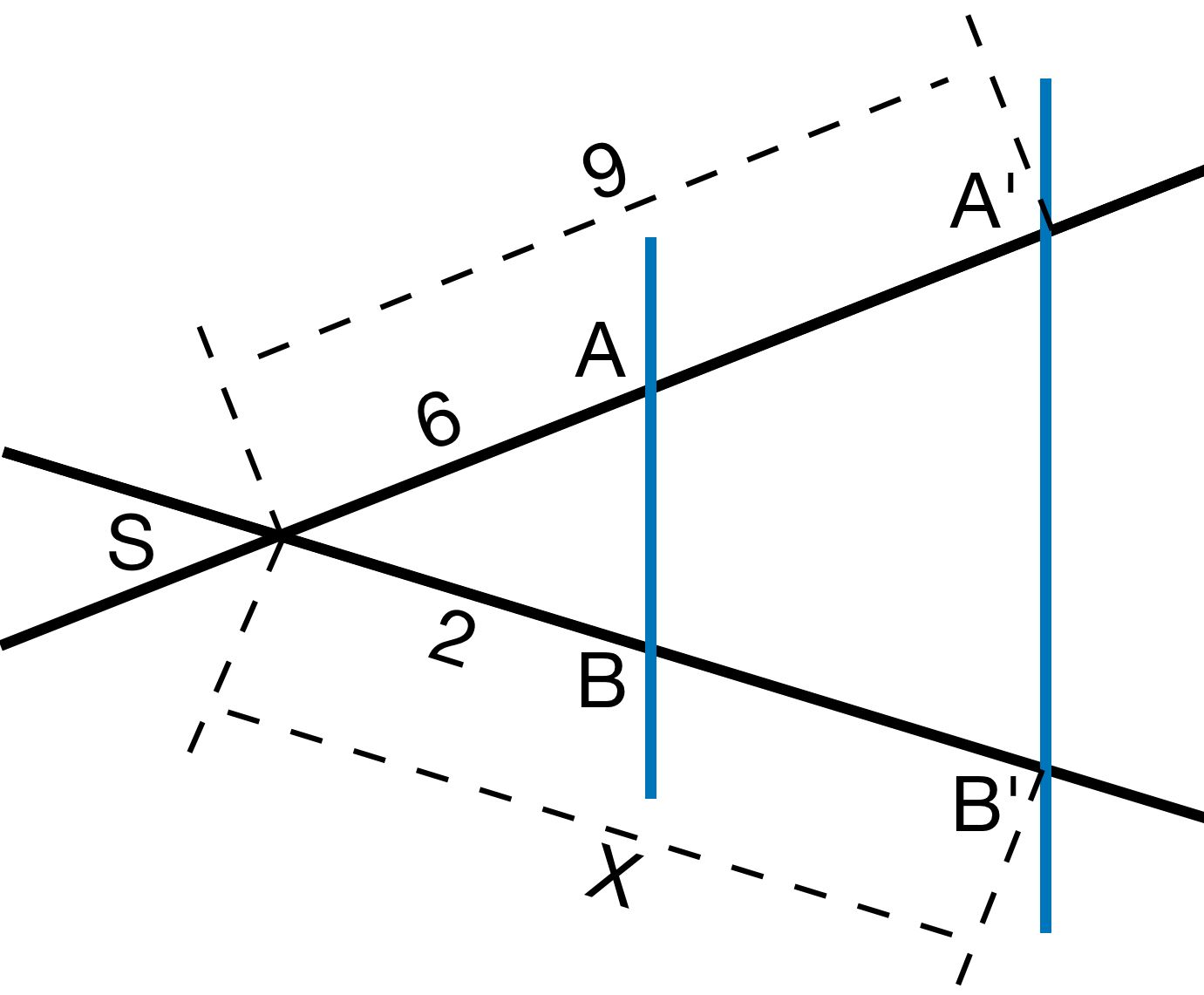
SBSB′=SASA′
2X=69 |⋅2
X=69⋅2
X=3
2X=69 |⋅2
X=69⋅2
X=3
Die Strecke SB′ ist also 3cm lang.
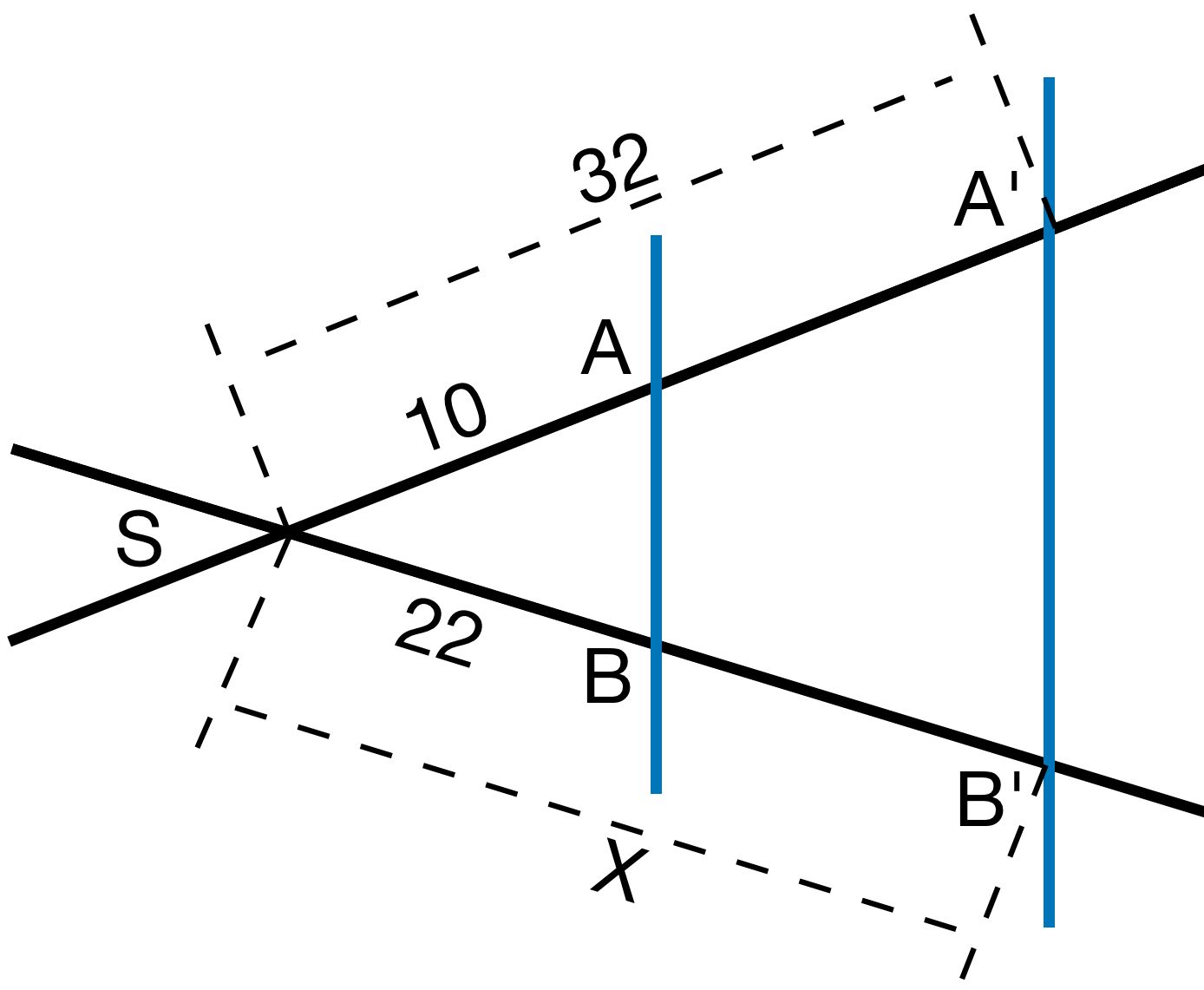
a)
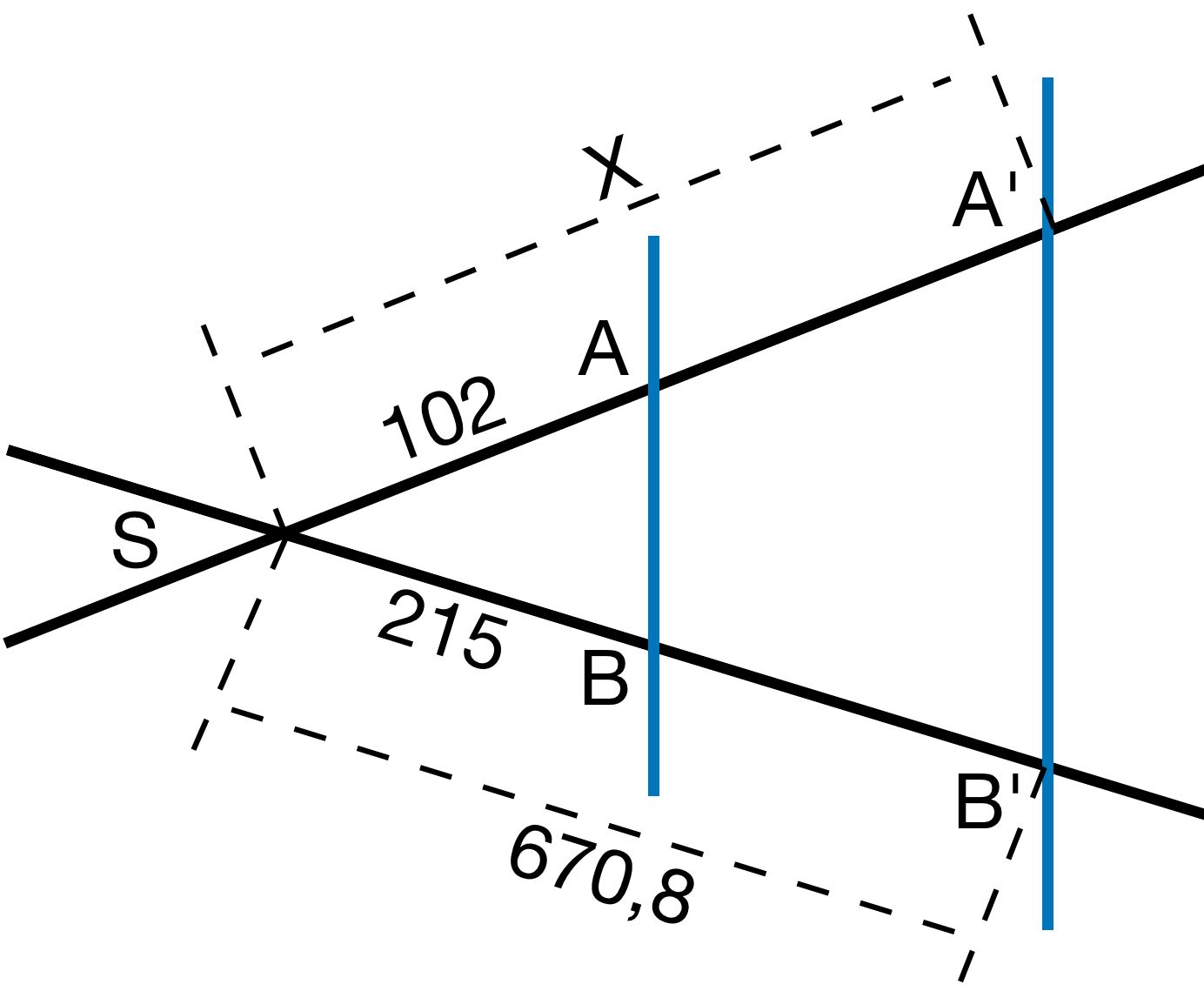
b)
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/f4c00744
https://editor.mnweg.org/entdecken/dokument/f4c00744
AB
1. Strahlensatz umstellen
Mathematik Flächen R 9
c)
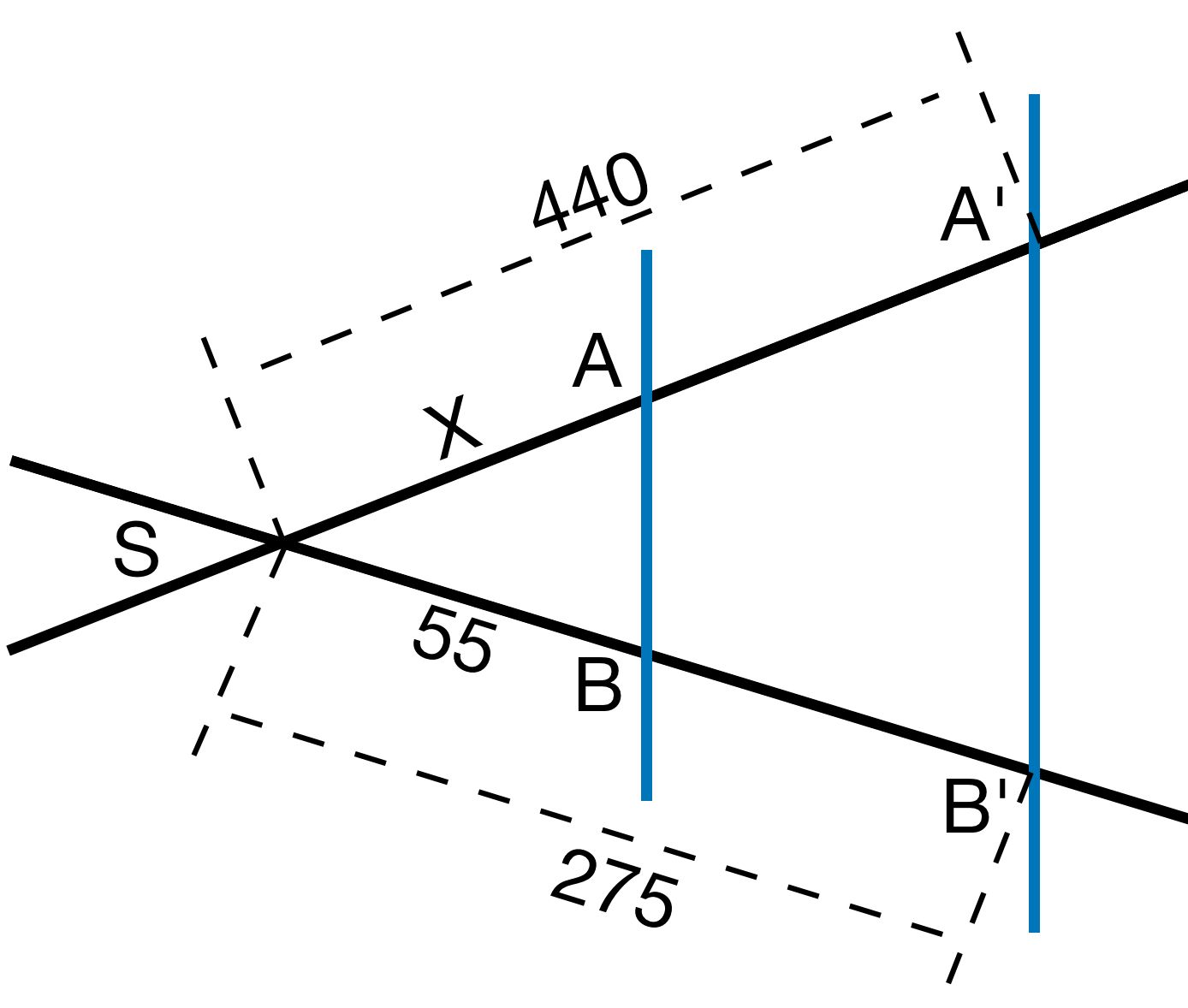
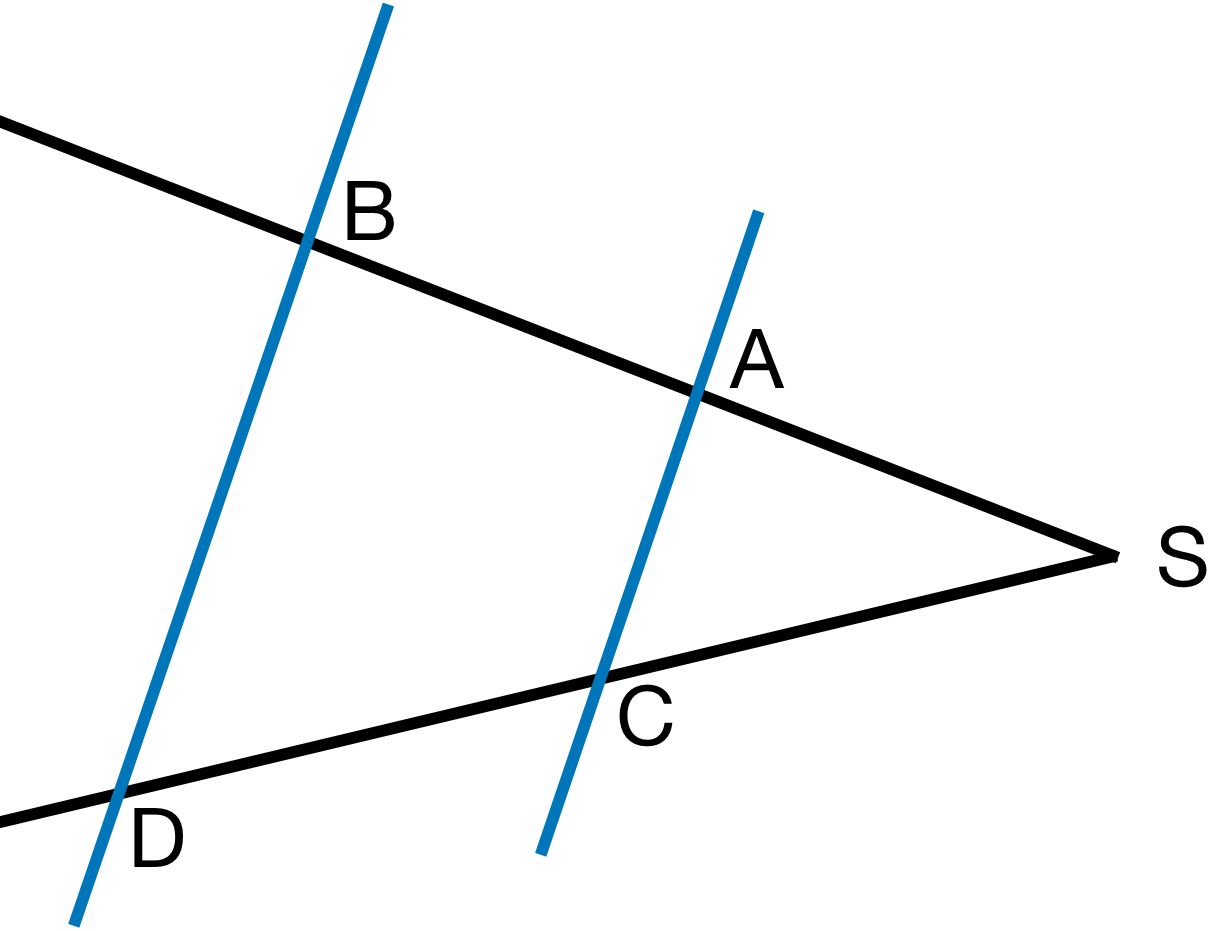
2
Gegeben:
SB=4,7cm
SC=2,2cm
SD=6cm
SC=2,2cm
SD=6cm
Gesucht: Länge der Strecke SA
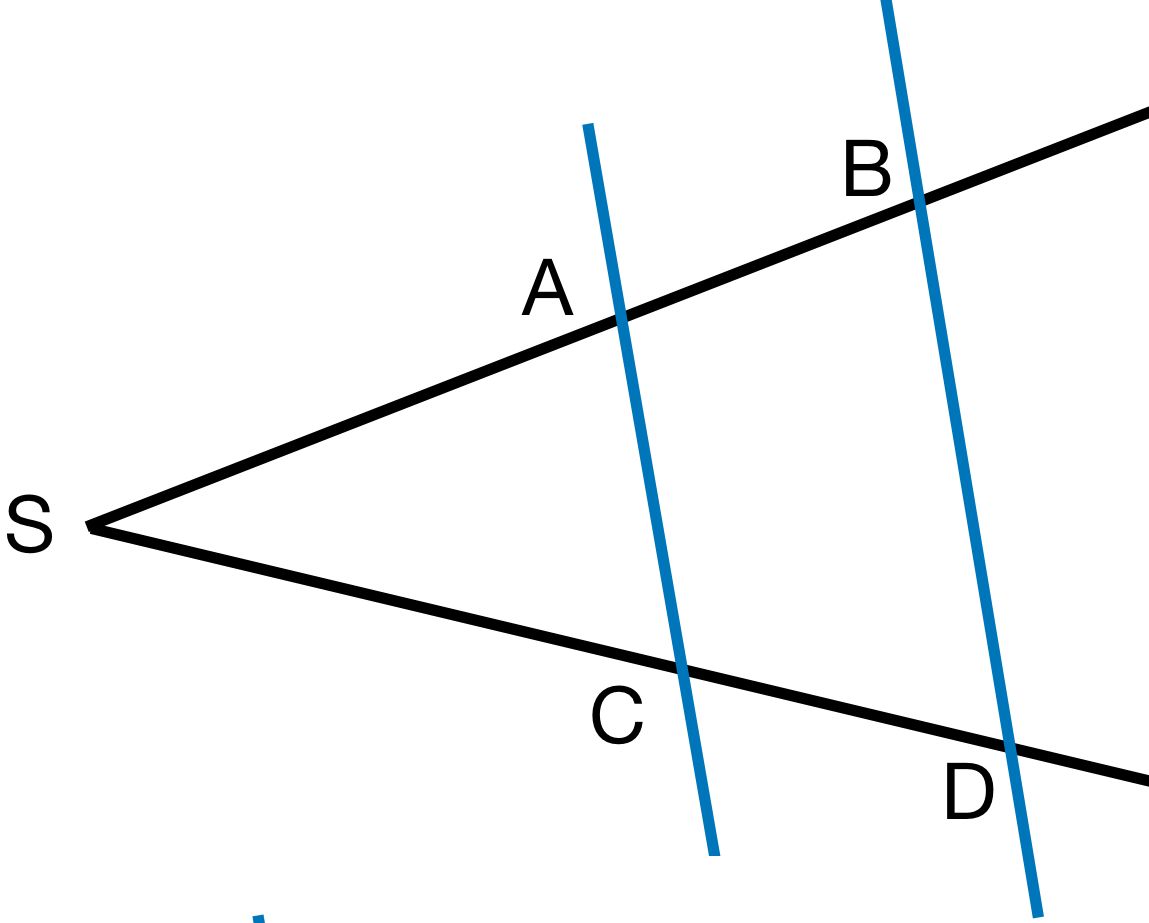
3
Gegeben:
SA=750cm
SC=825cm
CD=550cm
SC=825cm
CD=550cm
Gesucht: Länge der Strecke AB
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/f4c00744
https://editor.mnweg.org/entdecken/dokument/f4c00744


