Quadratische Funktionen mit Schiebereglern anzeigen
Erstelle mit GeoGebra den Graphen einer quadratischen Funktion f mit f(x)=ax2+bx+c, die mit drei Schiebereglern verändert werden kann. Dadurch soll die Parabel parallel zur x- oder y-Achse verschoben, gestaucht oder gestreckt werden. Der jeweilige Funktionsterm soll angezeigt werden.
Lösung:
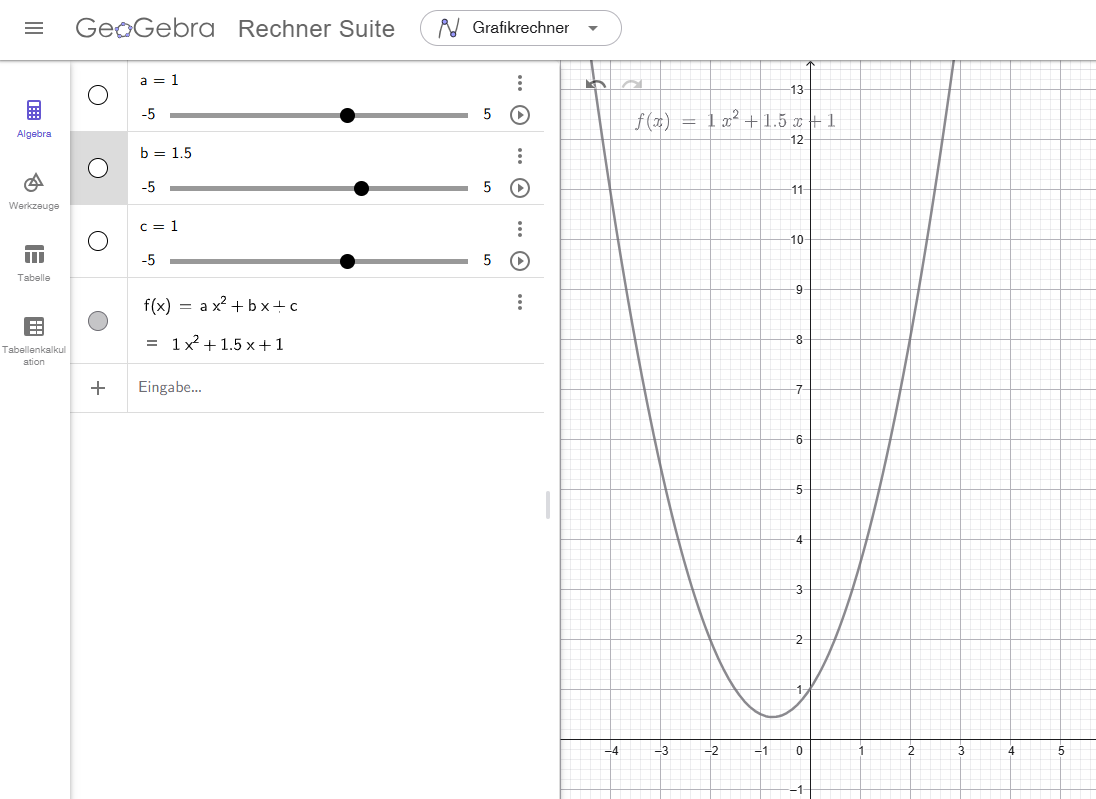
https://editor.mnweg.org/entdecken/dokument/geogebra-und-quadratische-funktionen-modul-2
Quadratische Funktion in der Scheitelpunktform anzeigen
Erstelle mit GeoGebra den Graphen einer quadratischen Funktion in Scheitelpunktform, die mit drei Schiebereglern verändert werden kann. Dadurch soll die Parabel parallel zur x- oder y-Achse verschoben, gestaucht oder gestreckt werden. Der jeweilige Funktionsterm und der Scheitelpunkt sollen angezeigt werden.
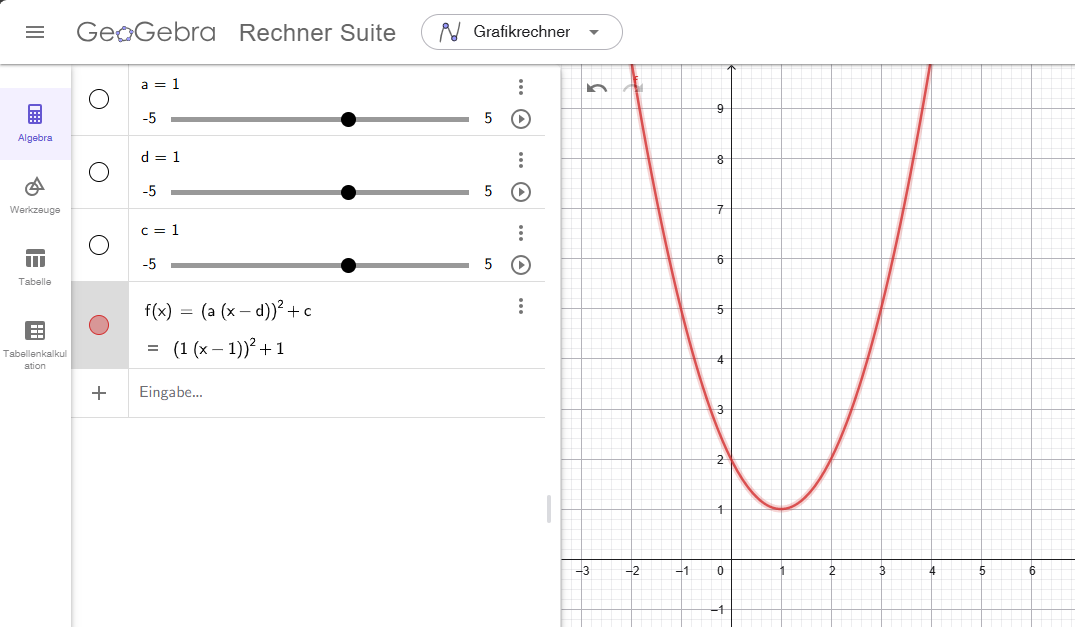
https://editor.mnweg.org/entdecken/dokument/geogebra-und-quadratische-funktionen-modul-2
Nullstellen
Ermittle die Nullstellen der folgenden quadratischen Funktionen und notiere sie dir:
a) f(x) = x² - 4 b) g(x) = x² - 4 x c) h(x) = 2x² + 4x d) i(x) = x² -10x + 9
Lösung:
Nullstellen mit Parametern
Gegeben ist die quadratische Funktion f mit f(x) = x² + 8x + r für x∈R und r∈R
Gib für r jeweils eine reelle Zahl an, sodass f
a) zwei Nullstellen
b) genau eine Nullstelle
c) keine Nullstelle hat.
Lösung:
https://editor.mnweg.org/entdecken/dokument/geogebra-und-quadratische-funktionen-modul-2
Schnittpunkte zweier Funktionen
Bestimme jeweils die Schnittpunkte der zwei Funktionen f und g und notiere:
a) f1(x) = x² - 4 b) f2(x) = x² - 4 x c) f3(x) = 2x² + 4x d) f4(x) = x² -10x + 9
g1(x) = - x² + 3 g2(x) = x² + 5 g3(x) = - 2x² - 1 g4(x) = x² + 1
Lösungen:
https://editor.mnweg.org/entdecken/dokument/geogebra-und-quadratische-funktionen-modul-2


