Plötz­lich bricht die Zom­bie­apo­ka­lyp­se aus! Es be­ginnt mit einem ein­zi­gen Zom­bie, der pro Stun­de zwei wei­te­re Men­schen in­fi­ziert. Jeder neue Zom­bie tut es ihm gleich.





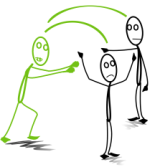
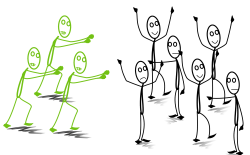
Frage: Wie viele Men­schen sind nach 5 Stun­den be­reits zu Zom­bies ge­wor­den?



Über­le­ge kurz, ver­su­che einen Term auf­zu­stel­len und schau dir auf der nächs­ten Seite die Ant­wort an...







Ant­wort: Nach einer Stun­de hat der erste Zom­bie zwei Men­schen in­fi­ziert.

→ Nach einer Stun­de gibt es drei Zom­bies.



In der nächs­ten Stun­de greift jeder der drei Zom­bies zwei wei­te­re Men­schen an. Ins­ge­samt sind das $3\cdot 2=6$ wei­te­re Men­schen.

→ Nach zwei Stun­den gibt es neun Zom­bies.



Nach drei Stun­den wird es folg­lich $9\cdot 2=18$ wei­te­re Zom­bies und ins­ge­samt 27 Zom­bies geben.

Man er­kennt, dass die An­zah­len (3, 9, 27) Drei­er­po­ten­zen sind. Es liegt daher nahe, dass die Funk­ti­ons­glei­chung $B(t)=3^t$ heißt, wobei N die An­zahl der Zom­bies ist und t in Stun­den an­ge­ge­ben wird.

Das Er­geb­nis lau­tet also:

In­ner­halb von 5 Stun­den gibt es $B(5)=3^5=243$ Zom­bies.



Frage: Wie lange dau­ert es, bis ganz Eu­ro­pa (742,5 Mil­li­o­nen Men­schen) zu Zom­bies wurde (mit Ta­schen­rech­ner)? Ver­su­che, das Er­geb­nis aus­zu­rech­nen und schaue auf der nächs­ten Seite nach der Lö­sung!





Ant­wort: Ge­sucht ist der Zeit­punkt t, bei dem B(t)=742.500.000 gilt. Man setzt also den Funk­ti­ons­term gleich dem ge­ge­be­nen B(t) und löst nach t auf:



$742500000=3^t$



Mit­hil­fe des Ta­schen­rech­ners er­gibt sich:



$solve(742500000=3^t,t)$



t = 18,6 Tage



Auf eine ganze Zahl ge­run­det, lau­tet das Er­geb­nis:

Ganz Eu­ro­pa ist be­reits nach 19 Stun­den zom­bi­fi­ziert.





Der Wachs­tums­fak­tor a er­gibt sich aus der Än­de­rungs­ra­te. Im Ein­füh­rungs­bei­spiel war



$a=3$      (also ist  $a>1$)



Damit wird die For­mel für das ex­po­nen­ti­el­le Wachs­tum zu:



$B(t)=B_0\cdot (a{)}^t$



mit



B(t): Be­stand zum Zeit­punkt t

B(0): An­fangs­be­stand (also Be­stand zum Zeit­punkt 0)

a: Wachs­tums­fak­tor

t: Zeit in ge­ge­be­ner Ein­heit

Der Zer­falls­fak­tor er­gibt sich aus der Än­de­rungs­ra­te. Man sagt Zer­falls­fak­tor und nicht Wachs­tums­fak­tor, wenn $0<a<1.$



Damit wird die For­mel für den ex­po­nen­ti­el­len Zer­fall zu:



$B(t)=B_0\cdot (a{)}^t$



Ein Bak­te­ri­um teilt sich nach jeder Stun­de in zwei neue Bak­te­ri­en. Jedes wei­te­re Bak­te­ri­um teilt sich auch wie­der jede Stun­de. Wie viele Bak­te­ri­en sind es nach einem Tag (=24h)?



Über­le­ge kurz und schau dann auf der Fol­ge­sei­te nach der Lö­sung.

$B_0=1$

$a=2$

$t_1=24$



Man schreibt zu­nächst die ge­ge­be­nen Werte auf. Ge­sucht ist $B(t_1)=B(24)$.

Dann setzt man in die Funk­ti­ons­glei­chung



$B(t)=B_0\cdot a^t$



ein und be­rech­net den Wert.



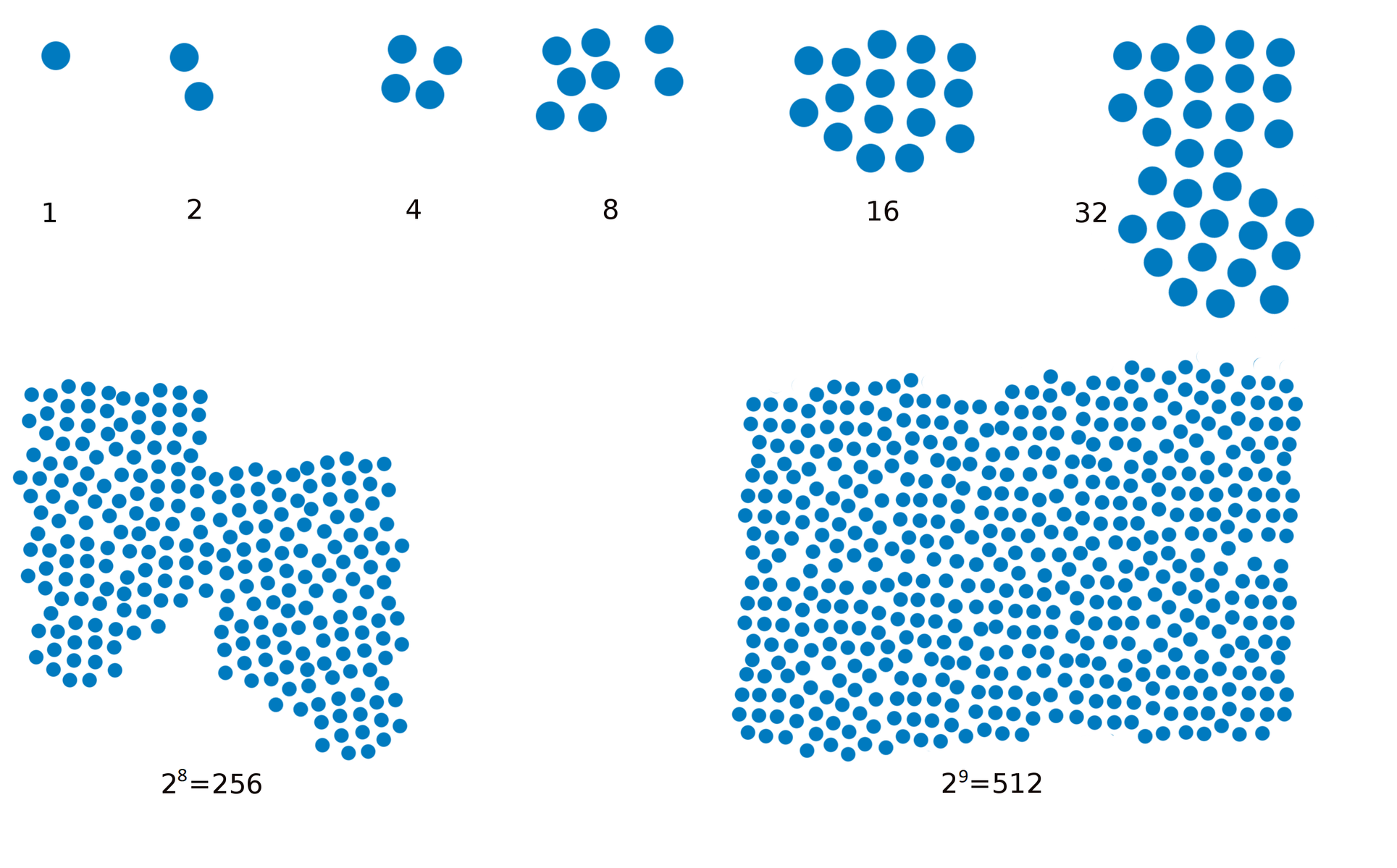
$B(24)=1\cdot 2^{24}=2^{24}=\mathrm{16.777.216}$



Nach einem Tag sind es also $\mathrm{16.777.216}$ Bak­te­ri­en.

Im Bild wird die stei­gen­de Wachs­tums­ge­schwin­dig­keit an­hand der zu den Bak­te­ri­en ge­hö­ren­den Funk­ti­ons­glei­chung $B(t)=2^t$ ver­deut­licht.

Man legt 500€ bei einer jähr­li­chen Ver­zin­sung von 3% an. Wie viel Geld hat man nach 5 Jah­ren?



B₀ = 500€

p = 3 % = 0,03

t₁ = 5 Jahre



Man schreibt zu­nächst die ge­ge­be­nen Werte auf. Ge­sucht ist N(t₁)=N(5).

Dann setzt man in die Funk­ti­ons­glei­chung ein und be­rech­net den Wert.



$B(5)=500\cdot (1+0,03{)}^5=500\cdot (1,03{)}^5=579,64$



Ant­wort: Nach 5 Jah­ren hat man also 579,64€.



Bei einem ra­dio­ak­ti­ven Stoff zer­fällt jedes Jahr 10% der noch vor­han­de­nen Masse. Be­rech­ne, wie viel nach 10 Jah­ren noch vor­han­den ist.



Wenn jedes Jahr 10 % zer­fal­len, dann sind im Um­kehr­schluss nach jedem Jahr noch 90 % vom Vor­jahr vor­han­den. Wir be­zeich­nen die Masse des Stof­fes im Jahr 0 mit m₀ , im Jahr 1 mit m₁ , im Jahr 2 mit m₂ …, im Jahr 10 mit m₁₀ .







$m_{10}=0,9\cdot m_9=0,9^{10}\cdot m_0\approx 0,3487\cdot m_0$



Ant­wort: Nach 10 Jah­ren sind also etwa 34,87% des ur­sprüng­li­chen Ma­te­ri­als vor­han­den.