Einstieg
Manche Alltagsgegenstände haben annähernd die Gestalt eines Kegels. Hier ein paar Beispiele:



Ein Kegel ist
ein dreidimensionaler Körper, der entsteht, wenn man
alle Punkte eines Kreises
mit einem Punkt außerhalb der Kreisebene
verbindet.
Der richtige Ausdruck für diesen Körper ist eigentlich Kreiskegel. In der höheren Mathematik werden nämlich manchmal auch Kegel betrachtet, deren Grundfläche kein Kreis ist.
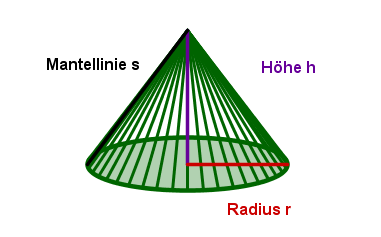
In der Schule geht es in der Regel um gerade Kreiskegel. Bei geraden Kreiskegeln liegt die Spitze des Kegels senkrecht über dem Mittelpunkt der Grundfläche.
Bemerkung:
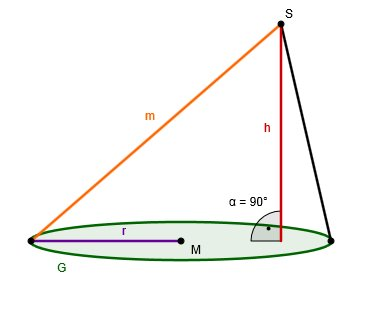
Ein gerader Kreiskegel entsteht, wenn sich ein rechtwinkliges Dreieck um eine seiner Seiten dreht.
Der entstehende Rotationskörper ist ein gerader Kreiskegel.
Es gibt aber auch schiefe Kreiskegel, wie z.B. der rechts dargestellte Kegel.
https://editor.mnweg.org/entdecken/dokument/kegel-dqbj7mzv
Volumen eines Kegels
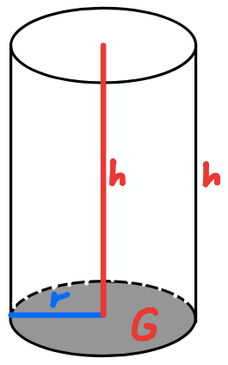
Das Volumen eines Zylinders kennst du bereits. Hier nochmal zur Wiederholung:
VZylinder=AG⋅h=π⋅r2⋅h
Schau dir folgendes Video an und überlege dir, wie man das Volumen eines Kreiskegels berechnet (den Teil mit der Kugel kannst du ignorieren, der folgt später):
Fülle den folgenden Lückentext aus:
Wenn ich einen Kegel und einen Zylinder mit gleicher und gleicher betrachte, dann füllt der Inhalt eines Kegels genau des Inhalts eines Zylinders. Damit beträgt die Formel für den Flächeninhalt des Kegels:
VKegel= ·Ag·h= ·π·r2·h
https://editor.mnweg.org/entdecken/dokument/kegel-dqbj7mzv
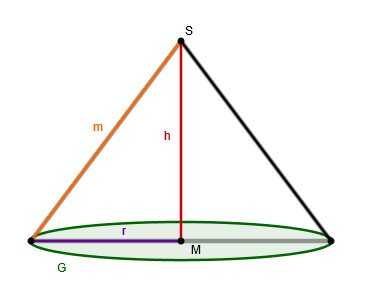
Das Volumen eines Kegels berechnet sich wie folgt:
VKegel=31⋅AG⋅h=31⋅π⋅r2⋅h
mit
AG: Grundfläche des Kegels
h: Höhe des Kegels
r: Radius der Grundfläche G des Kegels
Warum ist das so?
Die Grundfläche AG eines Kegels ist ein Kreis. Die Fläche von einem Kreis erhält man mit der Formel AKreis=π⋅r2
Schau in deinem Tafelwerk nach den Formeln!
https://editor.mnweg.org/entdecken/dokument/kegel-dqbj7mzv
Beispiel
Es ist Sommer und du kaufst ein Eis. Du erinnerst Dich, dass bei Eispackungen im Supermarkt die Menge an Eis in Litern angegeben ist. Das bringt Dich dazu, das Volumen in deiner Eistüte bestimmen zu wollen!
Nach Deiner Messung ist die Eistüte (hier: ein Kegel!) 16cm hoch und die Öffnung hat einen Durchmesser von 6cm. Wie viel Liter Eis befinden sich darin?
Lösung
Du benötigst den Radius r und die Höhe h des Kegels. Die Höhe ist direkt gegeben und der Radius ist der halbe Durchmesser:
Berechne damit nun das Volumen.

d =
r =
h =
VKegel=31⋅AG⋅h=31⋅π⋅r2⋅h=31⋅π⋅(3cm)2⋅16cm=151cm3
Antwort: Die Eistüte hat ein Volumen von cm3 bzw. ml.
https://editor.mnweg.org/entdecken/dokument/kegel-dqbj7mzv
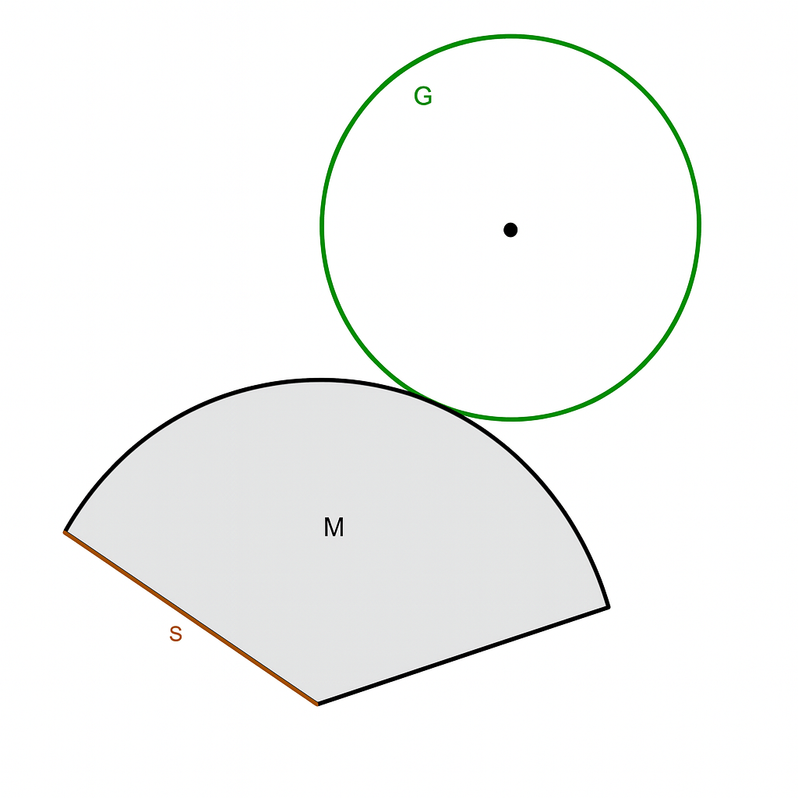
Oberflächeninhalt eines Kegels
Schau dir dazu folgendes Video an:
Der Oberflächeninhalt AO eines Kegels berechnet sich wie folgt:
AO=AG+AM
AG=π⋅r2
AM=π⋅r⋅s
Also:
AO=π⋅r2+π⋅r⋅s=π⋅r(r+s)
mit
AO: Oberflächeninhalt des Kegels
AG: Grundfläche des Kegels
AM: Mantelfläche des Kegels
s: Mantellinie am Kegel
r: Radius der Grundfläche des Kegels
Schau in deinem Tafelwerk nach den Formeln!
Warum ist das so? (Achtung: Nerdwissen!)
Die Grundfläche G eines Kegels ist ein Kreis . Die Fläche von einem Kreis erhält man durch die Formel AKreis=π⋅r2
Die Mantelfläche M eines Kegels ist ein Kreissektor mit Radius s. Die Fläche von diesem Kreissektor erhält man durch die Formel AMantel=π⋅s2⋅360α
Dabei ist α der Mittelpunktswinkel des Kreissektors. Dieser verhält sich zu 360° wie die Kreisbogenlänge, hier 2⋅π⋅r, zum gesamten Umfang eines Kreises mit Radius s. Also ergibt sich für die Mantelfläche:
AMantel=2⋅π⋅s2⋅π⋅r⋅π⋅s2=sr⋅π⋅s2=π⋅r⋅s
https://editor.mnweg.org/entdecken/dokument/kegel-dqbj7mzv
Beispiel
Betrachte den geraden Kegel. Der Radius der Grundfläche ist r=3cm und die Mantellinie s beträgt s=6cm.
Berechne den Oberflächeninhalt des Kegels.
Lösung
r =
s =
AO=π⋅r2+π⋅r⋅s=π⋅(3cm)2+π⋅3cm⋅6cm=84,8cm2
Antwort: Der Oberflächeninhalt des Kegels beträgt .
https://editor.mnweg.org/entdecken/dokument/kegel-dqbj7mzv


