Klasseneinteilung
Häufig stecken wir bestimmte Menschen in Schubladen, weil es unser Leben erleichtert. Dass dies nicht unbedingt gut ist, wurde hoffentlich im Ethik- oder Reliunterricht hinreichend besprochen. In der Statistik jedoch ist das anders. Hier ist es oft das einzige Mittel besonders großen Datensätzen Herr zu werden. Dass dies zu Fehlern führen kann, nimmt man billigend in Kauf. Was tut man nicht alles für die Übersichtlichkeit.
Beispiel
Betrachten wir ein Beispiel, bei dem wir fast schon wieder ethische Bedenken haben. Wir kategorisieren Menschen in Untergewicht, Normalgewicht, Übergewicht und Adipositas (Fettleibigkeit). Dies kann man mit Hilfe des sogenannten BMI (body mass index) machen. Er berechnet sich:
BMI = l2m , wobei m die Masse in kg und l die Körpergröße in m ist.
Menschen mit einem BMI von weniger als 18,5 haben Untergewicht, bis 25 ist Normalgewicht, bis 30 Übergewicht und ab 30 Adipositas.
Es ergeben sich mathematisch also folgende Klassen (Intervalle):
[0; 18,5[ [18,5;25[ [25;30[ und [30;[
Betrachten wir nun eine Messreihe der BMI von 10 Schülern: 203; 175; 314; 235; 273; 257; 194; 328; 229; 183
Nun ordnen wir die Liste und teilen sie in Klassen ein:
BMI
0-18,5
18,5-25
25-30
> 30
Ergebnisse
17,5; 18,3
19,4; 20,3; 22,9; 23,5
25,7; 27,3
31,4; 32,8
Absolute Anzahl
2
4
2
2
Um größere Datensatze zu kategorisieren, kann man sie in Klassen einteilen. Klassen sind offene oder geschlossene Intervalle zum Teil unterschiedlicher Größe.
https://editor.mnweg.org/entdecken/dokument/klasseneinteilung-und-histogramme
Histogramme
Eine weitere graphische Darstellung von Daten sind Histogramme. Sie ähneln dem Säulendiagramm, berücksichtigen jedoch die Klassenbreite.
Beispiel
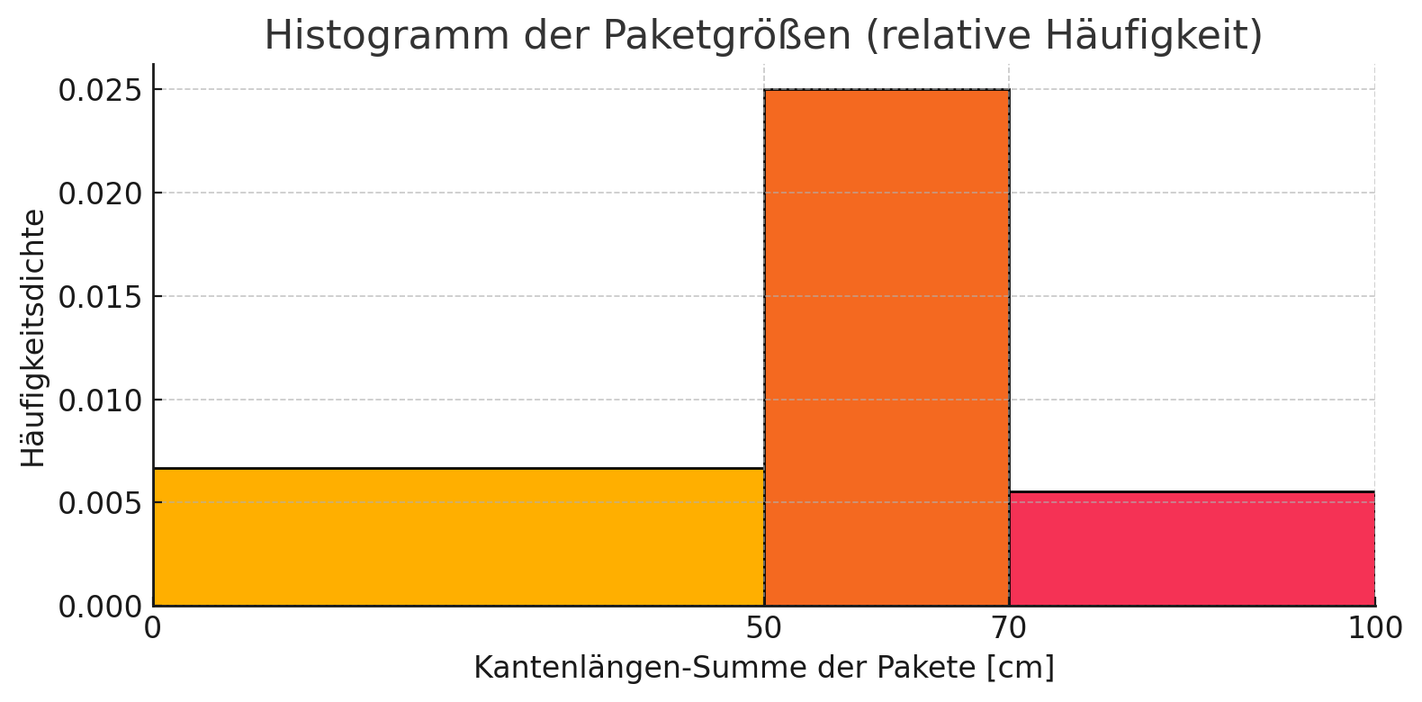
Ein Paketdienstleister teilt die zu versendenden Pakete in drei Klassen ein. Es wird jeweils die Summe aus der längsten und der kürzesten Kante gebildet. Paketgröße S haben Pakete mit einer Summe von 50cm, M von 70cm und L bis 1m. (Größere Pakete werden nicht versandt.)
Ein Paketshop hat folgenden Tagesversand an Paketen mit einer Kantenlängensumme in cm.
47; 57; 95; 43; 56; 74; 21; 45; 63; 36; 57; 61; 83; 55; 55; 67; 33; 57
Hier die Zahlenfolge sortiert von klein nach groß:
21 ; 33 ; 36 ; 43 ; 45 ; 47 ; 55 ; 55 ; 56 ; 57 ; 57 ; 57 ; 61 ; 63 ; 67 ; 74 ; 83 ; 95
Ein Klasseneinteilung sieht dann wie folgt aus:
Größe
S
M
L
Intervall
0cm-50cm
50cm-70cm
70cm-100cm
Klassenbreite
50
20
30
Absolute Häufigkeit
6
9
3
Relative Häufigkeit
186=31
189=21
183=61
Häufigkeitsdichte =
KlassenbreiteRelativeHa¨ufigkeit
31:50=1501=0,0067
21:20=401=0,025
61:30=1801=0,006
https://editor.mnweg.org/entdecken/dokument/klasseneinteilung-und-histogramme
Quartile
Im letzten Kapitel haben wir festgestellt, dass der Median häufig der Wert ist, der eine Messreihe am besten charakterisiert, da er unauffällig gegen Ausreißer ist. Dennoch ist es gerade bei umfangreichen Messreihen nicht sinnvoll, diese nur durch einen einzigen Lageparameter zu charakterisieren. Deshalb hat man sich überlegt, jeweils den Median der unteren und der oberen Hälfte der geordneten Liste auch noch anzugeben. Man nennt sie oberes bzw. unteres Quartil (lat.: quartum oder vierte Teil). Der Median und die beiden Quartile teilen also die Messreihe nun in vier gleiche Teile.
Der Median der unteren oder oberen Hälfte einer geordneten Liste, heißt unteres Quartil qu bzw. oberes Quartil qo. Das untere Quartil lasst sich wie folgt berechnen:
Berechne 0,25∗n
1. Fall: Ist das Ergebnis keine natürliche Zahl, so runde auf. DU erhältst die Zahl i. qu=xi
2. Fall: Ist das Ergebnis eine natürliche Zahl, so ist i=0,25∗n
qu=2xi+xi+1
Beispiel
Betrachten wir eine Messreihe mit n = 7 Werten, so ergibt sich für das untere Quartil:
0,25∗n=0,25∗7=1,75
i=2
qu=x2
Besitzt eine Messreihe n = 9 Werte, so ergibt sich:
0,25∗n=0,25∗9=2,25
i=3
qu=x3
Wir runden immer auf!
Liegt hingegen eine Messreihe mit n = 8 Werten vor, so rechnen wir:
0,25∗n=0,25∗8=2
i=2
i+1=3
qu=2x2+x3
https://editor.mnweg.org/entdecken/dokument/klasseneinteilung-und-histogramme
Boxplots
Nun haben wir so viele Parameter kennengelernt. Da kann man leicht die Übersicht verlieren. Deshalb gibt es die sogenannten Boxplots. Dabei handelt es sich um Diagramme, die die Lageparameter aus dem letzten Kapitel übersichtlich darstellen. Minimum, Maximum, Median und die beiden Quartile werden für das Erstellen eines Boxplots benötigt. Machen wir uns also an die Arbeit.
Beispiel
Bei den Olymischen Spielen 2012 in London ergab sich folgende Rangliste beim Kugelstoßen der Manner:
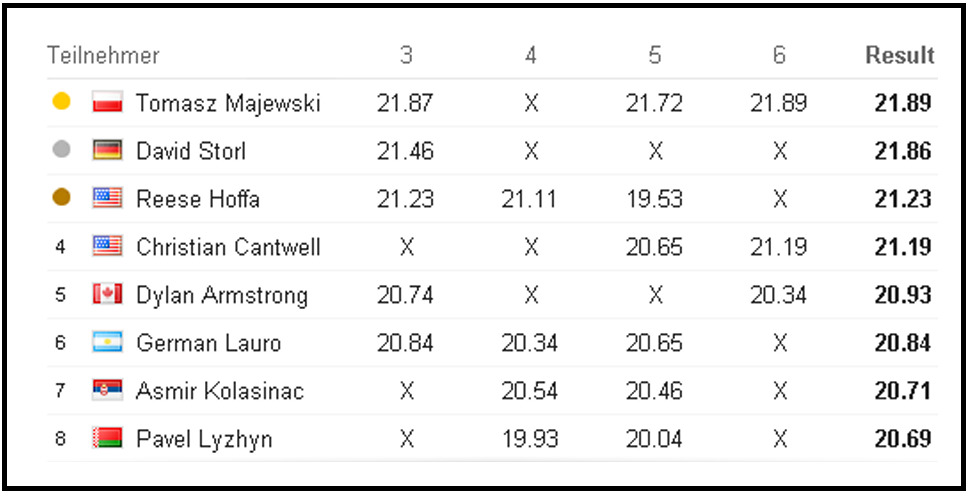
Wir sortieren natürlich von klein nach groß. So ergibt sich: 20,69; 20,71; 20,84; 20,93; 21,19; 21,23; 21,86; 21,89
Die Liste hat acht Werte, sodass sich fur die Lageparameter folgendes ergibt:
z=2x4+x5=220,93+21,19=21,06
xmin=20,69
qu=2x2+x3=220,71+20,84=20,78
qo=2x6+x7=221,86+20,93=21,55
Nun können wir den Boxplot erstellen.
https://editor.mnweg.org/entdecken/dokument/klasseneinteilung-und-histogramme
Der Boxplot ist die grafische Darstellung der wesentlichen Informationen einer Messreihe. Er besteht aus einer Box und sogenannten Whiskers (engl.: Barthaare, Schnurrhaare). Die Box reicht vom unteren bis zum oberen Quartil. Ihre Breite ist frei wählbar. Der Median wird mit einer waagrechten roten Strecke innerhalb der Box gekennzeichnet. Die Whiskers erstrecken sich vom unteren Quartil zum Minimum und vom oberen Quartil zu Maximum. Eine vertikale Achse gibt wie beim Koordinatensystem die Skalierung an.
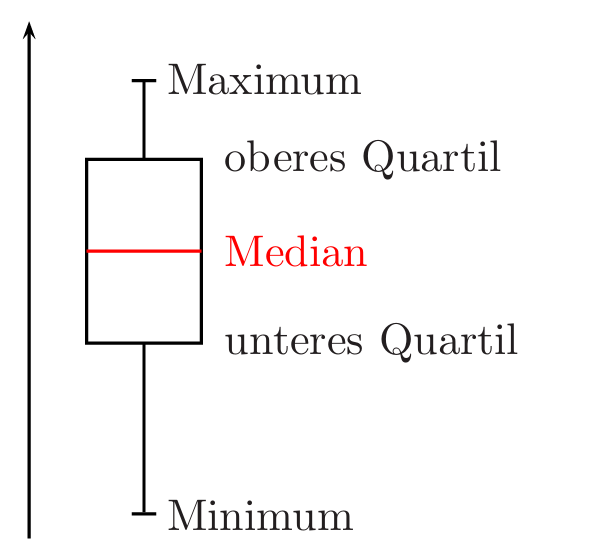
Um den Boxplot für unsere Kugelstoßer zu zeichnen, wählenwir für 0,1m auf dem Rasen 5mm, also ein Kästchen auf dem Papier. Außerdem nehmen wir auch nur den Ausschnitt, der uns wirklich interessiert. Wir fangen dementsprechend nicht bei 0m, sondern bei 20,6m an.
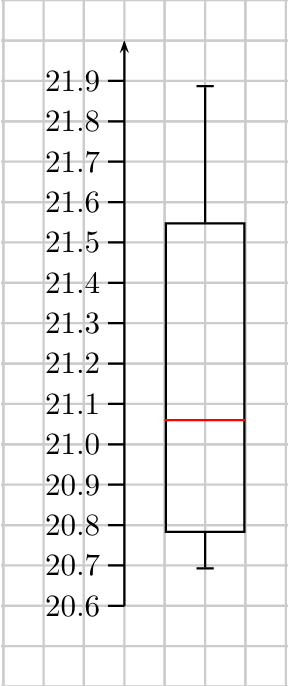
https://editor.mnweg.org/entdecken/dokument/klasseneinteilung-und-histogramme


