Wo stehe ich?

$\Rightarrow$ Erstelle eine ABC-Liste zu allen bisher relevanten Begriffen zum Thema Geraden und
Ebenen im Raum.

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X,Y

Z

Wo stehe ich?

$\Rightarrow$ Vergleiche deine Liste mit einem Arbeitspartner und ergänze fehlende Begriffe.

$\Rightarrow$ Erläutere die Bestandteile einer Ebenengleichung in Parameterform.

Gib ein Beispiel an.

Ebenengleichungen lassen sich mithilfe eines Stützvektors und zwei Spannvektoren aufstellen. Diese Form der Darstellung heißt Parametergleichung einer Ebene, da sie zwei Parameter enthält.

Der Vorteil dieser Darstellung ist, dass sie sehr anschaulich ist.

Eine alternative Darstellungsform von Ebenen ist die Koordinatengleichung, mit der viele Rechnungen einfacher und schneller ausgeführt werden können.

Zum Aufstellen der Koordinatengleichung genügen bereits ein Stützvektor und ein zur Ebene senkrechter (orthogonaler) Vektor, der Normalenvektor.

Durch die beiden Vektoren wird die Lage der Ebene auch eindeutig festgelegt.

Aber wieso ist das so?

Zum Ausprobieren

Nimm dir zwei Gegenstände: Einen Vektor z.B einen Stift mit einem flachen Ende und eine Ebene z.B. ein Buch oder dein Tablet.

\Rightarrow

Halte deinen Vektor in einer beliebigen aber festen Position in die Luft.

\Rightarrow

Halte die Ebene an das spitze Ende deines Vektors. Auf wie viele mögliche Arten kannst du die
Ebene an den Vektor halten?

\Rightarrow

Drehe deinen Stift um und halte das Ende des Vektors so, dass das flache Ende komplett auf
der Ebene aufliegt. Wie stehen Ebene und Vektor jetzt zueinander?

\Rightarrow

Verändere die Position des Vektors und mache das ganze noch einmal.

\Rightarrow

Wie viele verschiedene Neigungen kann eine Ebene haben, wenn ein Vektor senkrecht auf
ihr steht?

Du hast vermutlich festgestellt, dass wenn du die Ebenen an die spitze Seite des Stiftes hältst, es viele verschieden Ausrichtungsmöglichkeiten gibt. Hältst du die Ebene an die flache Seite des Stiftes, so dass beide senkrecht zueinander stehen, gibt es nur eine mögliche Position der Ebene. Der senkrechte Normalenvektor legt also die Ausrichtung der Ebene eindeutig fest.

Da ein Vektor ja keine feste Position im Koordinatensystem beschreibt sondern nur eine bestimmte Richtung und Länge, kann der Normalenvektor an jedem beliebigen Punkt des Koordinatensystems beginnen. Seine Position und damit auch die der Ebene ist also noch nicht eindeutig bestimmt. Es sind viele parallele Ebenen möglich. Um die Ebene eindeutig zu bestimmen benötigen wir also noch den Stützvektor (Punkt der auf der Ebene liegt).

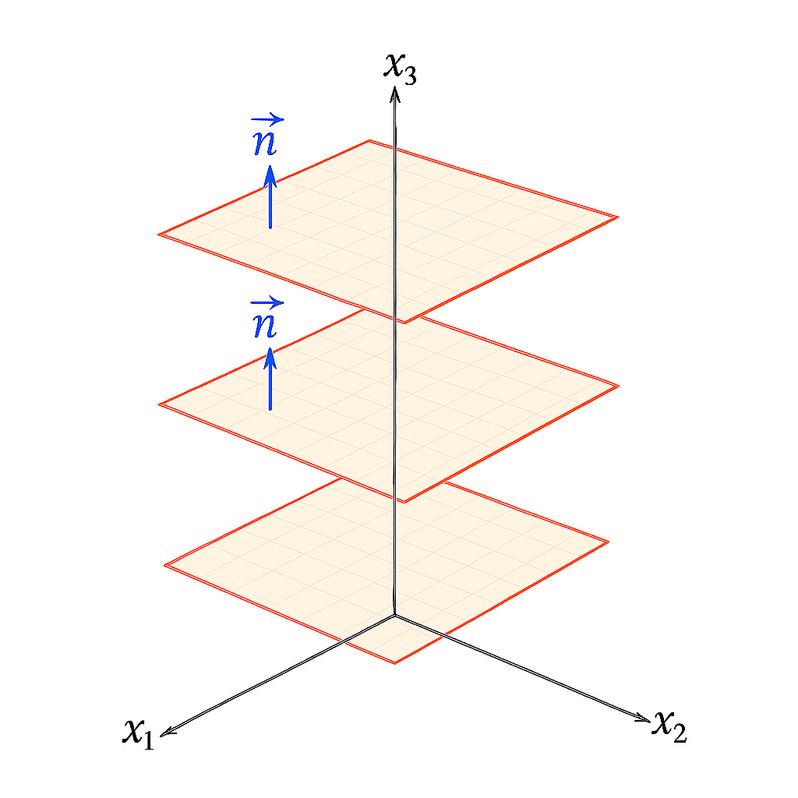
Die allgemeine Form der Koordinatengleichung

Die allgemeine Form der Koordinatengleichung lautet:

$E : n_{1} x_{1} + n_{2} x_{2} + n_{3} x_{3} = d$

Dabei sind $x_{1}$ , $x_{2}$ und $x_{3}$ die Koordinaten eines beliebigen Punktes $X (x_{1} ∣ x_{2} ∣ x_{3})$ , der in der Ebene liegt.

$n_{1}$ , $n_{2}$ und $n_{3}$ sind die Koordinaten eines Normalenvektors der Ebene $n = n_{1} n_{2} n_{3}$ .

Der Normalenvektor ist ein Vektor, der senkrecht auf der Ebene steht und damit die die Neigung der Ebene angibt. Der Wert $d$ beschreibt die genaue Position der Ebene im Koordinatensystem. So haben parallele Ebenen den gleichen Normalenvektor, aber unterschiedliche Werte für $d$ .

Um $d$ zu bestimmen, werden die Koordinaten eines beliebigen Punktes, der in der Ebene liegt, in die Koordinatengleichung eingesetzt.

Die Koordinatengleichung einer Ebene aus Stützvektor und Normalenvektor bestimmen

Beispielaufgabe

Die Ebene enthält den Punkt P(2/-4/1) und ist orthogonal zu $n = 5 - 2 1$ . Gib eine Koordinatengleichung von E an.

Rechenweg

Die Koordinaten des Normalenvektors werden in die Koordinatengleichung eingesetzt:

$E : n_{1} x_{1} + n_{2} x_{2} + n_{3} x_{3} = d$ also $E : 5 x_{1} - 2 x_{2} + 1 x_{3} = d$ .

Der Stützvektor der Ebene $a = 2 - 4 1$ führt zu einem Punkt, der in der Ebene liegt. Seine Koordinaten können daher für $x_{1}$ , $x_{2}$ und $x_{3}$ eingesetzt werden, um $d$ zu berechnen:

$5 \cdot 2 - 2 \cdot (- 4) + 1 \cdot 1 = d$ $\Rightarrow d = 19$

Der Wert von $d$ wird in die Ebenengleichung eingesetzt. Nun liegt die Ebene als Koordinatengleichung vor:

$E : 5 x_{1} - 2 x_{2} + 1 x_{3} = 19$

Punkte in der Ebene bestimmen

Beispielaufgabe

Gib drei Punkte an, die in

E : 2 x_{1} + 2 x_{2} + 1 x_{3} = 8

Rechenweg

Setze Werte für $x_{1}, x_{2} u n d x_{3}$ ein, so dass die Gleichung erfüllt ist.

Zum Beispiel $A (2/2/0)$ .

Was du auch immer tun kannst, ist zwei der drei Koordinaten gleich null setzen und nur die dritte Koordinate berechnen. Zum Beispiel $B (0/0/8) o d er C (0/4/0)$ .

Normalenvektor aus Koordinatengleichung bestimmen

Beispielaufgabe

Gib den Normalenvektor der Ebene

E : - 3 x_{1} + 5 x_{2} - 4 x_{3} = - 3

an.

Rechenweg

Der Normalenvektor entspricht den Koeffizienten von $x_{1}, x_{2} u n d x_{3}$ .

Es gilt also $n = - 3 5 - 4$

Können zwei unterschiedliche Koordinatengleichungen zu identischen Ebenen gehören?

Koordinatengleichungen dürfen wie andere Gleichungen umgeformt werden, indem sie mit einem Faktor multipliziert werden. Die beiden folgenden Ebenengleichungen beschreiben daher identische Ebenen.

$E_{1} : 2 x_{1} + 3 x_{2} - 2 x_{3} = - 4$

$E_{2} : 4 x_{1} + 6 x_{2} - 4 x_{3} = - 8$

$E_{1}$ wurde mit dem Faktor 2 multipliziert, um $E_{2}$ zu erhalten.

Wie wird mit einer Koordinatengleichung eine Punktprobe gemacht?

Um zu prüfen, ob ein Punkt in der Ebene liegt, werden seine Koordinaten in die Koordinatengleichung eingesetzt. Nur wenn sich daraus eine wahre Aussage ergibt, liegt der Punkt in der Ebene.

Beispielaufgabe

Untersuche, ob die Punkte $P (- 4∣2∣1)$ und $Q (0∣1∣2)$ in der Ebene

$E : 2 x_{1} + 3 x_{2} - 2 x_{3} = - 4$ liegen.

Rechenweg

Untersuchung von P

Die Koordinaten des Punktes $P$ werden in die Ebene eingesetzt:

$2 \cdot (- 4) + 3 \cdot 2 - 2 \cdot 1 = - 4$

$- 4 = - 4 ✓$

Die Aussage ist wahr. Der Punkt $P$ liegt in der Ebene $E$ .

Untersuchung von Q

Die Koordinaten des Punktes $Q$ werden in die Ebene eingesetzt:

$2 \cdot 0 + 3 \cdot 1 - 2 \cdot 2 = - 4$

$- 1 \neq = - 4$

Die Aussage ist falsch. Der Punkt $Q$ liegt nicht in der Ebene $E$ .