Einstieg
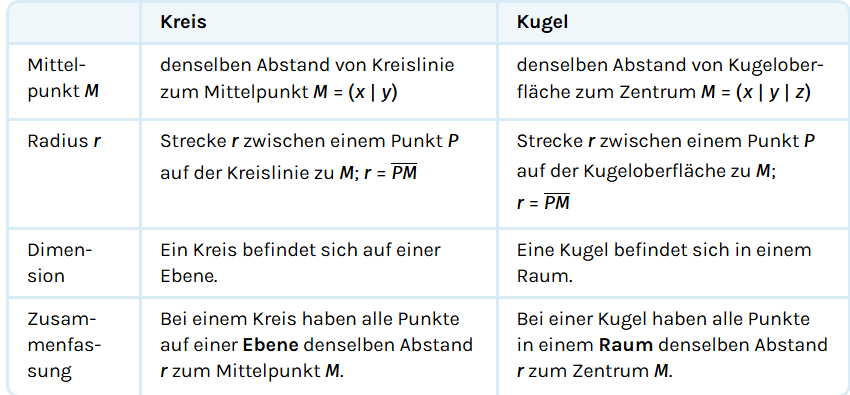
Eine Kugel ist im dreidimensionalen Raum das, was im zweidimensionalen Raum ein Kreis ist.
Jede Kugel hat einen Mittelpunkt M. Alle Punkte auf der Kugeloberfläche haben den gleichen Abstand zu M. Dieser Abstand r heißt Radiuslänge.

Vergleich von Kreis und Kugel
https://editor.mnweg.org/entdecken/dokument/kugel-e0zlxavj
Volumen einer Kugel
Das Volumen einer Kugel lässt sich auf Basis des Volumens eines Zylinders herleiten. Wie das geht, erfährst du hier:
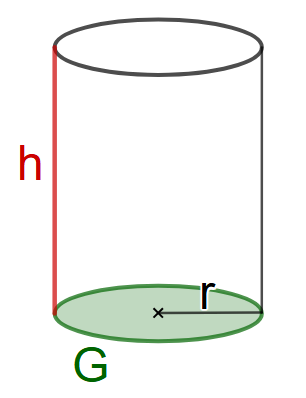
Im anderen Kapitel hast du bereits gelernt, wie man das Volumen eines Zylinders berechnet. Die allgemeine Formel dazu lautet:
VZylinder=AG⋅h=π⋅r2⋅h
Schau dir folgendes Video an und überlege dir anschließend, wie man das Volumen einer Kugel berechnet:
Fülle den folgenden Lückentext aus:
Wenn ich eine Kugel, einen Kegel und einen Zylinder mit gleicher betrachte, dann passt in eine Kugel so viel Flüssigkeit wie in einen Kegel. Außerdem füllt der Inhalt der Kugel des Inhalts vom Zylinder.
Damit beträgt die Formel für den Flächeninhalt des Kegels:
VKugel= ·Ag·h= ·π·r2·h
Die Formel kann ich jetzt noch ein bisschen vereinfachen: Die Höhe einer Kugel beträgt dem Zweifachen des Radius einer Kugel, d.h. h = ·r. Wenn ich das jetzt in die Formel oben einsetze, kommt folgendes heraus:
VKugel= ·π·r2·2r= ·π·r3
https://editor.mnweg.org/entdecken/dokument/kugel-e0zlxavj
Volumen einer Kugel
Wenn man wissen möchte, wie groß der Rauminhalt einer Kugel ist, so muss man das Volumen berechnen.
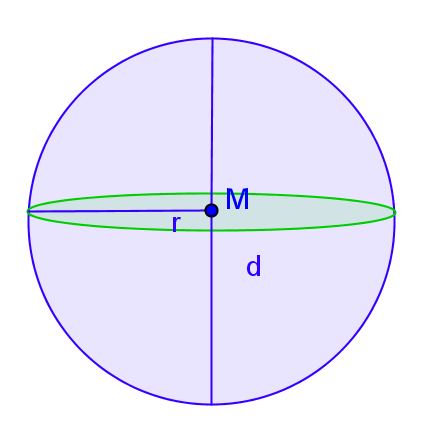
Das Volumen einer Kugel berechnet sich wie folgt:
VKugel=34⋅π⋅r3
Beispiel
Berechne das Volumen einer Billardkugel, die einen Durchmesser d von 57,2 mm hat.
Bevor du deinen gegebenen Wert sofort in die neue Formel einsetzt, musst du dir klarmachen, dass sich ein Kreis und eine Kugel hinsichtlich Radius und Durchmesser nicht unterscheiden.

r=2d=257,2mm=28,6mm
VBillardkugel=34⋅π⋅(28,6mm)3=97991mm3≈98cm3
Antwort: Das Volumen der Billardkugel beträgt .
https://editor.mnweg.org/entdecken/dokument/kugel-e0zlxavj
Oberflächeninhalt einer Kugel
Vereinfacht kann man sich eine Oberfläche wie einen Mantel vorstellen, der sich um die geometrische Figur legt. Eine Zeitungsseite kann so zu einem Kegel geformt werden, wenn man sie rollt. Diese Fläche ergibt die Oberfläche.
Wenn man nun die Kugel in Farbe eintaucht, so markiert man dessen Oberflächeninhalt. Mithilfe dieser Fläche kann man z. B. ausrechnen, wie viel Gold man braucht, damit man die Kugel auf der Dachspitze vom Olympiaturm vergolden kann.
Experiment
Schau dir das Video zum Experiment an!
Material je Gruppe:
- 1 Orange
- Lineal
- Weißes A4 Papier
- Stift
Schält die Orange und zerteilt sie in 2 Hälften.
Legt eine Hälfte mit der flachen Seite nach unten auf ein Blatt Papier und zeichnet einen Kreis. Malt ihn mit dickem Stift nach.
Nehmt die Schale und legt euren Kreis mit den Schalenstückchen aus. Legt so, dass möglichst keine Lücken und keine Überlappungen entstehen.
Ihr habt noch Schale übrig? Dann zeichnet einen weiteren Kreis und fahrt fort wie in Schritt 3, bis alle Schalenstückchen eurer Orange in Kreisen ausgelegt wurden.
Notiert, wie viele Kreise ihr mit der Schale einer Orange auslegen konntet.
Vergleicht mit den anderen Gruppen. Wie lautet die Formel für den Oberflächeninhalt einer Kugel in Abhängigkeit von r?
Wir haben herausgefunden, dass man mit den Orangenschalen insgesamt Kreise ausfüllen kann. Der Flächeninhalt eines Kreises kann mit folgender Formel berechnet werden:
AK= Damit beträgt die Formel für den Oberflächeninhalt einer Kugel: AO= ·πr2.
https://editor.mnweg.org/entdecken/dokument/kugel-e0zlxavj
Der Oberflächeninhalt einer Kugel berechnet sich wie folgt:
AO=4⋅π⋅r2
Beispiel
Ein offizieller Basketball hat einen Oberflächeninhalt von 1809,56 cm2. Wie groß ist dann der Radius r?

OBasketball=4⋅π⋅r2
Stelle zunächst nach dem Wert r2 um.
r2=4πAO
Ziehe anschließend die Wurzel
r=4πOBasketball
Setze die gegebenen Werte ein
r=4π1809,56cm2=12cm
Antwort: Der Radius eines Basketballs beträgt also .
Schau dir auch unbedingt das Video zur Kugel vom DorFuchs an:
https://editor.mnweg.org/entdecken/dokument/kugel-e0zlxavj


