TitelLineare Funktionen
AutorRobert.klonner
veröffentlicht28.10.2025
FachMathematik
KompetenzbereichFunktionen
NiveaustufeM (Mindeststandard)
Phase9
MaterialformArbeitsblatt

Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

Schreibe die Funktionsgleichungen für A und B auf.
Denke an das Steigungsdreieck.

Tipp

Die Steigung findest du, indem

du von einem zum nächsten

Kästchenschnittpunkt gehst.

Zeichne einen Graphen zu der Funktionsgleichung f(x) = - 0,5 x - 1 für die x-Werte - 4 bis + 4.
Tipp: Es genügt, wenn du zwei Punkte berechnest. Am besten keine Nachbarpunkte!

Welcher Buchstabe gehört zu welcher Funktion?
Schreibe den richtigen Buchstaben in die Tabelle vor die Funktion.

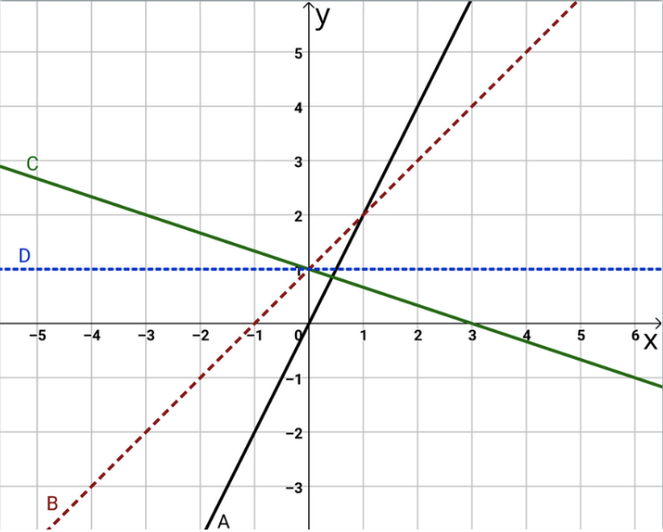
f(x) = 2 x

f(x) = - $\frac{1}{3}$ x + 1

f(x) = 1

f(x) = x + 1

Welcher Buchstabe gehört zu welcher Funktion?
Schreibe den richtigen Buchstaben in die Tabelle vor die Funktion. Ergänze am Ende die fehlende Funktion.

f(x) = $\frac{1}{3}$ x + 3

f(x) = - 3

f(x) = 4 x - 1

Ergänze die Wertetabelle. Die Funktionsgleichung lautet: f(x) = - 2x + 1,5

- 2

- 1

f(x) = y

- 0,5

In Tiengen kannst du von verschiedenen Anbietern
einen E-Roller ausleihen. In der entsprechenden APP
findest du drei unterschiedliche Angebote.
Welches Angebot würdest du wählen, wenn du im Monat die E-Roller etwa 125 Minuten nutzen würdest?

Angebot A

Gesamtkosten incl. 100 Min./Monat

40 €

jede weitere

Minute 50 Cent

Angebot B

Grundgebühr

15 €/Monat

Preis pro

Minute 35 Cent

Angebot C

Keine

Grundgebühr

Preis pro

Minute nur

45 Cent

Reflektionsfragen

Bevor du mit den Aufgaben beginnst, solltest du kurz über die folgenden Fragen nachdenken. Wenn du zu einer Frage keine Idee hast, lies noch einmal in der INFO nach, sprich mit anderen Lernpartner:innen darüber oder frage deine Lernbegleitung.

$\Rightarrow$ Unter welcher Voraussetzung steigt der Graph einer linearen Funktion?

$\Rightarrow$ Was ist der Unterschied zwischen einer linearen und einer proportionalen Funktion?

$\Rightarrow$ Wie kann der Graph einer linearen Funktion nach unten verschoben werden?

$\Rightarrow$ Welche Informationen eignen sich, um die Funktionsgleichung einer linearen Funktion bestimmen zu können?

$\Rightarrow$ Was kann daraus geschlussfolgert werden, wenn zwei lineare Funktionen die gleiche Steigung $a$ haben?

$\Rightarrow$ Mit welchem Vorgehen lässt sich der Schnittpunkt zweier Geraden bestimmen?

Die Abbildungen zeigen die linearen Funktionen

f (x) = x + 1

g (x) = x - 1

und

h (x) = - x - 1

. Ordne die Funktionsgleichungen den Graphen zu.

Gib die Funktionsgleichungen der linearen Funktionen an, deren Graphen im Koordinatensystem dargestellt wurden.

Gegeben ist die Funktion

f (x) = 2 x - 1

. Ermittle die Funktionsgleichung der Funktion mit den beschriebenen Eigenschaften.
a) Der Graph der Funktion

g (x)

enthält den Punkt

P (0∣3)

und verläuft parallel zum Graphen von

f (x)

.
b) Der Graph der Funktion

h (x)

schneidet den Graphen der Funktion

f (x)

senkrecht im Punkt

Q (3∣5)

.
c) Der Graph der Funktion

k (x)

schneidet die Funktion

f (x)

bei

x = 2

und hat die Nullstelle

x = 6

Die Höhe einer brennenden Kerze kann mit der Funktion

h (t) = - 0, 5 t + 12

beschrieben werden (alle Angaben in cm). Dabei ist

t

die Zeit in Stunden.
a) Bestimme die Höhe der Kerze nach 5 Stunden.
b) Ermittle die Gesamtbrenndauer der Kerze.