Wiederholung: Lineare Funktionen

Schau dir das Video von Daniel Jung und das Video vom DorFuchs an:

Lineare Funktionen, Übersicht | Mathe by Daniel Jung

YouTube-Video

Lineare Funktionen (Mathe-Song DorFuchs )

YouTube-Video

Merke

Eine Lineare Funktion hat die allgemeine Funktionsgleichung:

Das Schaubild zeigt eine Gerade mit der Steigung m.

Der Schnittpunkt der Geraden mit der y-Achse ist im Punkt (0|b).

Folglich wird b als y-Achsenabschnitt bezeichnet.

y = m · x + n

Beispiel

Worte: Eine Pizza Margerita kostet 4,00 € jede weitere Zutat kostet 0,50 €.

Wertetabelle:

Schaubild:

Funktionsgleichung:

x

0

1

2

3

4

5

6

y

4,0

4,5

5,0

5,5

6,0

6,5

7,0

Frage

Wie viel

kostet eine

Pizza mit

Pilzen,

Peperoni,

Salami,

Oliven und Kapern?

Lösung

y = 0,5x + 4

Hier sagt die Steigung aus, wie viel der Grundpreis von 4 € pro weitere Zutat x steigt.

Merke

Die Steigung wird mit m bezeichnet und mit den Koordinaten eines Punktes P (x|y)

und folgender Formel berechnet:

m = \frac{Δ y}{Δ x}

Berechnung

Aus der Wertetabelle oder dem Schaubild kannst du die Koordinaten einzelner Punkte entnehmen:

Der Quotient ist immer gleich!

x

1

2

3

4

5

6

y

2

4

6

8

10

12

m = \frac{Δ y}{Δ x} = \frac{4 - 2}{2 - 1} = \frac{6 - 4}{3 - 2} = \frac{8 - 6}{4 - 3} = 2

Zeichnung

Mit Hilfe eines "Steigungsdreiecks"

zeichnest du die Steigung m

in das Schaubild (= Koordinatensystem) ein:

m = \frac{Δ y}{Δ x} = \frac{2}{1} = 2

Beachte:

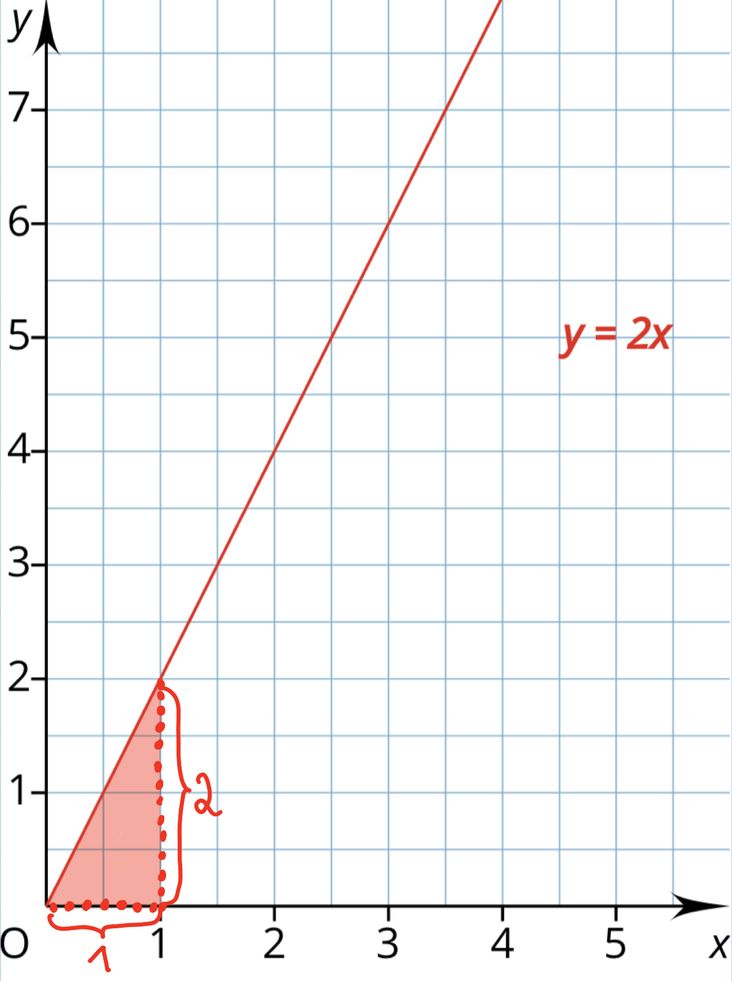
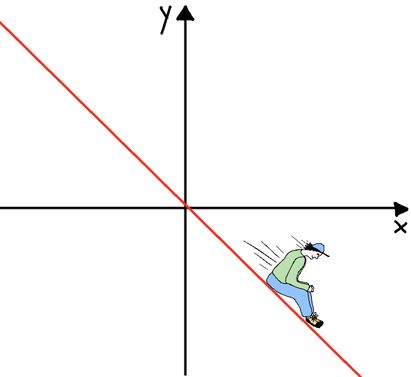
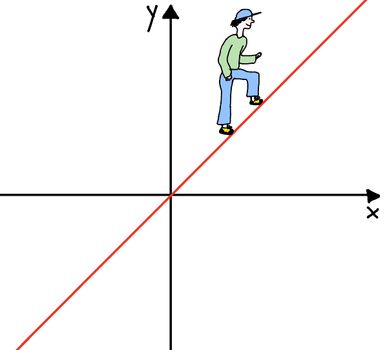
Die Steigung kann positiv oder negativ sein.

z . B . : m = 2

z . B . : m = - 2

Lineare Funktionen verstehen und lösen

Der Graph einer linearen Funktion ist immer eine Gerade.

Merkwissen zu linearen Funktionen

- Die Funktionsgleichung lautet: f(x) = mx + n

- Die Steigung m gibt an, ob die Gerade steigt oder fällt

$\to$ m $>$ 0 $\to$ die Gerade steigt

$\to$ m $=$ 0 $\to$ die Gerade ist parallel zur x-Achse

$\to$ m $<$ 0 $\to$ die Gerade fällt

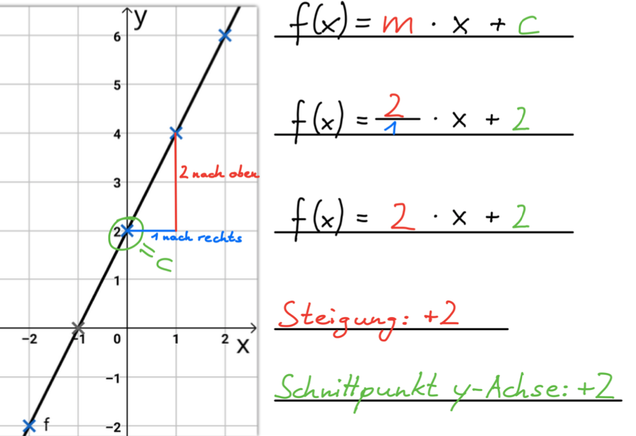
- Die Variable n (wird manchmal auch als c oder b geschrieben) gibt den y-Achsenabschnitt an, an dem die Gerade die

y-Achse (y = n) schneidet.

Also z.B. n = 2 $\to$ Schnittpunkt (0|2)

- Mit Hilfe des sogenannten Steigungsdreieckes kann man die Steigung einzeichnen.

- Lineare Funktionen können als Funktionsgleichung, in einer Wertetabelle oder als Graph dargestellt werden.

Mit dieser APP kannst du die linearen

Funktionen nochmals üben.

1

Übung 1:
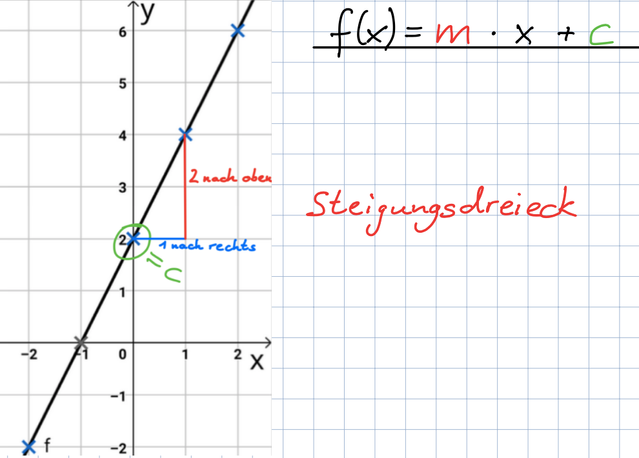
Hier siehst du den Graphen mit einem Steigungsdreieck. Überlege dir, welchen Wert n hat und wie groß die Steigung m ist. Schreibe die Funktionsgleichung auf.
Tipp: Lösung immer abdecken!

2

Übung 2:
Ergänze die Wertetabelle. Die Funktionsgleichung lautet: f(x) = 2x + 2

x

0

1

2

3

4

5

f(x) = y

6

8

3

Übung 3:
Hier siehst du einen weiteren Graphen. Überlege dir, welchen Wert c (bzw. n) hat und wie groß die Steigung m ist. Zeichne das Steigungsdreieck ein und schreibe die Funktionsgleichung auf.

4

Übung 4:
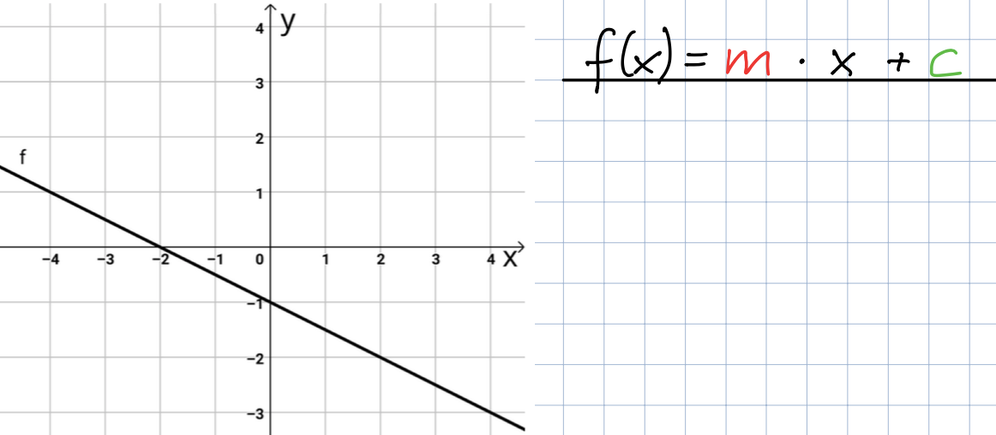
Hier siehst du drei verschiedene Graphen.
Schreibe den richtigen Buchstaben in die Tabelle
vor die jeweilige Funktion.
Zur Übung kannst du auch nochmal die Steigungsdreiecke einzeichnen.

Tipp

Die Steigung findest du, indem

du von einem zum nächsten

Kästchenschnittpunkt gehst.

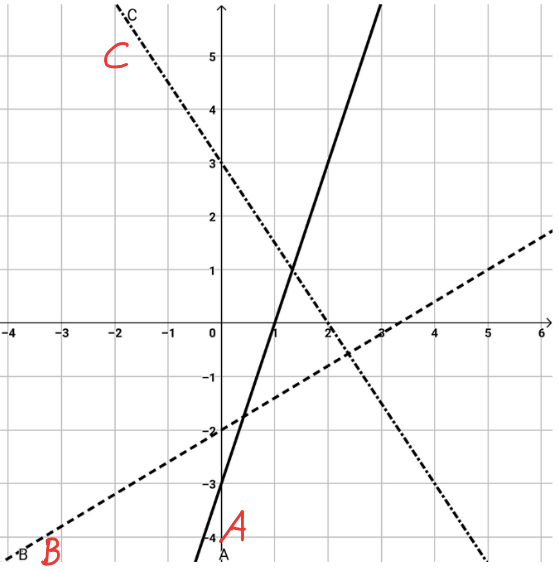
f(x) = $\frac{3}{5}$ x - 2 oder f(x) = 0,6 x - 2

f(x) = - $\frac{3}{2}$ x + 3 oder f(x) = - 1,5 x + 3

f(x) = 3x - 3

5

Übung 5:
Ergänze die Wertetabelle. Die Funktionsgleichung lautet: f(x) = -

\frac{1}{2}

x - 1

x

- 3

- 2

- 1

0

1

2

3

f(x) = y

Welchen Einfluss hat der $y$ -Achsenabschnitt $n$ auf den Verlauf einer linearen Funktion?

Die folgende Abbildung zeigt Funktionen der Form $y = 1 x + n = x + n$

Der $y$ -Achsenabschnitt $n$ gibt an, wo die $y$ -Achse geschnitten wird. Für $n > 0$ wird der Graph der Funktion nach oben verschoben. Für $n < 0$ wird der Graph der Funktion nach unten verschoben.

Wie lässt sich eine Geradengleichung aufstellen?

Um die Funktionsgleichung einer linearen Funktion zu bestimmen, müssen zwei Informationen bekannt sein. Als Informationen eignen sich Punkte der Funktion, die Steigung $m$ oder der

$y$ -Achsenabschnitt $n$ . Je nachdem, welche Informationen gegeben sind, ist ein unterschiedliches Vorgehen erforderlich.

Wenn der Graph der Funktion vorliegt, können die Informationen aus der Abbildung entnommen werden.

Beispielaufgabe

Bestimme die Funktionsgleichung der beschriebenen Funktion.

a) Der Graph der linearen Funktion $f (x)$ schneidet die $y$ -Achse bei $- 2$ und geht durch den Punkt $P (1∣2)$ .

b) Die Punkte $A (- 2∣3)$ und $B (4∣ - 3)$ liegen auf dem Graphen der linearen Funktion $g (x)$ .

Rechenweg

a) $f (x) = m x + n$

$n = - 2$

$f (x) = m x - 2$

$f (1) = 2$

$2 = m \cdot 1 - 2$

$a = 4$

$f (x) = 4 x - 2$

Die Steigung $a$ einer linearen Funktion lässt sich mit folgender Formel bestimmen, wenn zwei Punkte $P_{1} (x_{1} ∣ y_{1})$ und $P_{2} (x_{2} ∣ y_{2})$ gegeben sind:

$m = \frac{y _{2} - y _{1}}{x _{2} - x _{1}}$

b) $g (x) = m x + n$

$m = \frac{- 3 - 3}{4 - ( - ) 2} = - 1$

$g (x) = - 1 x + n$

$g (-2) = 3$

$3 = - 1 \cdot (- 2) + n$

$n = 1$

$g (x) = - 1 x + 1$

Wie lässt sich die Nullstelle einer linearen Funktion bestimmen?

Für die Bestimmung einer Nullstelle wird die Funktion gleich Null gesetzt. So entsteht eine Gleichung, die nach $x$ aufgelöst werden kann.

Beispielaufgabe

Berechne die Nullstelle der Funktion $f (x) = 4 x + 6$ .

Rechenweg

$f (x) 0 x = 0 = 4 x + 6 = - 1, 5$

Wie lässt sich anhand der Funktionsgleichungen erkennen, wie zwei Geraden zueinander liegen?

Zwei Geraden verlaufen parallel zueinander, wenn sie die gleiche Steigung $m$ haben. In allen anderen Fällen schneiden sie sich. Wenn sie sich senkrecht schneiden, ist das Produkt ihrer Steigungen $- 1$ .

Beispielaufgabe

Zeige, dass sich die Funktionen $f (x) = 2 x + 1$ und $g (x) = - 0, 5 x - 4$ senkrecht schneiden.

Rechenweg

$2 \cdot (- 0, 5) = - 1$

$\Rightarrow$ Die Geraden schneiden sich senkrecht.

Wie lässt sich der Schnittpunkt zweier Geraden bestimmen?

Um den Schnittpunkt zweier Geraden zu bestimmen, werden ihre Funktionsgleichungen gleichgesetzt. So entsteht eine Gleichung, die nach $x$ aufgelöst werden kann. Der Wert von $x$ wird in eine beliebige der beiden Funktionsgleichungen eingesetzt, um die $y$ -Koordinate des Schnittpunktes zu ermitteln.

Beispielaufgabe

Ermittle den Schnittpunkt der Funktionen $f (x) = 2 x + 1$ und $g (x) = - 0, 5 x - 4$ .

Rechenweg

$f (x) = g (x)$

$2 x + 1 = - 0, 5 x - 4$

$x = - 2$

$f (- 2) = - 3$

$S (- 2∣ - 3)$

Wie­der­ho­lung: Li­ne­a­re Funk­ti­o­nen

Li­ne­a­re Funk­ti­o­nen ver­ste­hen und lösen

Wiederholung: Lineare Funktionen

Lineare Funktionen verstehen und lösen