Schau dir zum Ein­stieg fol­gen­des Video an:

Du hast im Video ge­lernt, dass einen gro­ßen Un­ter­schied zwi­schen li­ne­a­rem, ex­po­nen­ti­el­len und qua­dra­ti­schem Wachs­tum gibt. Im Fol­gen­den wol­len wir uns ins­be­son­de­re mit dem Un­ter­schied zwi­schen li­ne­a­rem und ex­po­nen­ti­el­lem Wachs­tum be­schäf­ti­gen, da es in der Natur be­son­ders häu­fig vor­kommt.



An­hand zwei­er Pra­xis­bei­spie­le wol­len wir den Un­ter­schied klar­ma­chen:



• Bak­te­ri­el­les Wachs­tum

• Ver­meh­rung von Geld und Zin­ses­zins­rech­nung

Zu Be­ginn sind 10 Bak­te­ri­en vor­han­den. Das Wachs­tum soll 50 % be­tra­gen.



Wir un­ter­schei­den zwei Sze­na­ri­en:





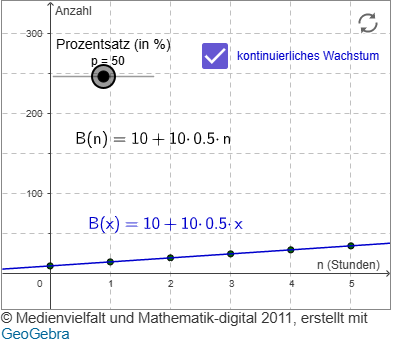
Sze­na­rio 1: Das Wachs­tum er­folgt li­ne­ar

Beim li­ne­a­ren Wachs­tum wird davon aus­ge­gan­gen, dass in jeder Stun­de eine gleich blei­ben­de An­zahl der ur­sprüng­li­chen An­zahl der Bak­te­ri­en B₀ hin­zu­kom­men.



In un­se­rem Bei­spiel ver­meh­ren sich die Bak­te­ri­en um 50 % der ur­sprüng­li­chen Bak­te­ri­en. Es kom­men also pro Stun­de 50 % von 10 Bak­te­ri­en = 5 Bak­te­ri­en hinzu.



Die Ver­meh­rung in den wei­te­ren Stun­den wird also immer nur von der ur­sprüng­li­chen Bak­te­ri­en­an­zahl B₀ aus be­rech­net.



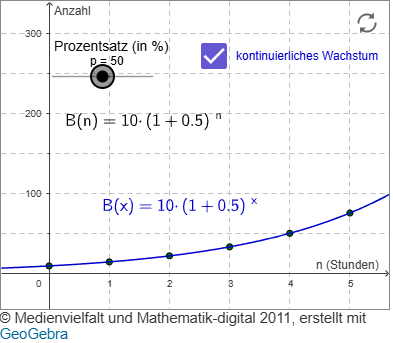
Sze­na­rio 2: Das Wachs­tum er­folgt ex­po­nen­ti­ell

Beim ex­po­nen­ti­el­len Wachs­tum nimmt die An­zahl der Bak­te­ri­en in jeder Stun­de um einen be­stimm­ten Pro­zent­satz der An­zahl in der vor­an­ge­gan­ge­nen Stun­de zu.



Das be­deu­tet, dass die Bak­te­ri­en­zahl B₀ in jeder Stun­de mit einem fes­ten Fak­tor mul­ti­pli­ziert wird.



In un­se­rem Bei­spiel ver­meh­ren sich die Bak­te­ri­en um 50 % pro Stun­de, be­zo­gen auf die vor­an­ge­gan­ge­ne Stun­de.

$+5$

$\cdot 1,5$

$\cdot 1,5$

$+5$

$\cdot 1,5$

$+5$

$\cdot 1,5$

$+5$

$\cdot 1,5$

$+5$

$\cdot 1,5$

$+5$

Du hast 1.000 EUR ge­spart. Das Ka­pi­tel soll sich um 3 % p.a. (lat. p.a. = per annum = pro Jahr) ver­meh­ren.



Wir un­ter­schei­den zwei Sze­na­ri­en:





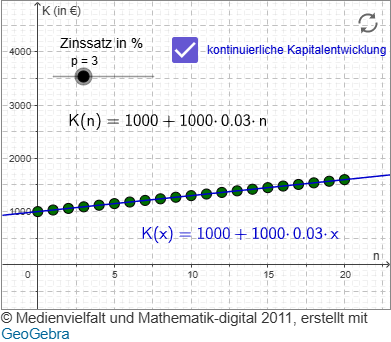
Sze­na­rio 1: Das Wachs­tum er­folgt li­ne­ar

Beim li­ne­a­ren Wachs­tum wird davon aus­ge­gan­gen, dass jedes eine gleich blei­ben­de Menge des ur­sprüng­li­chen Ka­pi­tals B₀ hin­zu­kommt.



In un­se­rem Bei­spiel ver­mehrt sich das Geld um 3 % des ur­sprüng­li­chen Ka­pi­tals. Es kom­men also pro Jahr 3 % von 1.000 EUR = 30 EUR hinzu.



Die Ver­meh­rung des Gel­des wird also immer nur vom ur­sprüng­li­chen Ka­pi­tal B₀ aus be­rech­net.



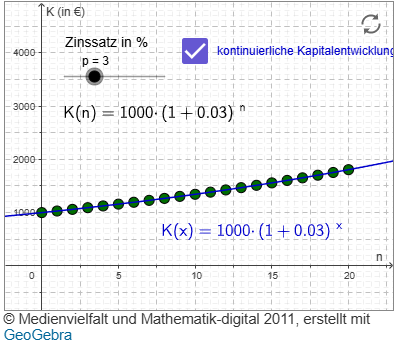
Sze­na­rio 2: Das Wachs­tum er­folgt ex­po­nen­ti­ell

Beim ex­po­nen­ti­el­len Wachs­tum nimmt die Menge der Gel­des jedes Jahr um einen be­stimm­ten Pro­zent­satz des Ka­pi­tals des vor­an­ge­gan­ge­nen Jah­res zu.



In un­se­rem Bei­spiel ver­mehrt sich das Ka­pi­tal um 3 % pro Jahr, be­zo­gen auf das Ka­pi­tal des vor­an­ge­gan­ge­nen Jah­res.

$\cdot 1,03$

$+30$

$+30$

$\cdot 1,03$

$+30$

$\cdot 1,03$

$+30$

$\cdot 1,03$

$\cdot 1,03$

$+30$

$\cdot 1,03$

$+30$

Bei­spiel:

$d=-1,2$

Bei­spiel:

Hier ist der Wachs­tums­fak­tor $a$ kon­stant, da $a=\frac{2,4}{1,6}=\frac{3,6}{2,4}=\frac{5,4}{3,6}=1,5$