TitelLösung: Mult/Div mit Zehnerpotenzen
AutorAnneFreudenberg
veröffentlicht26.01.2022
FachMathematik
KompetenzbereicheEinheiten, Rechnen

Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

Hinweis zum Einsatz im Unterricht

Mit dieser Datei kann nur das Lösungsblatt erzeugt werden.

Dezimalzahlen in der Stellenwerttafel

Übernimm die Tabelle 1 in dein Heft. Ergänze rechts die fehlenden Dezimalzahlen. Trage nun noch mindestens vier deiner gefundenen Zahlen aus Aufgabe 1 ein.

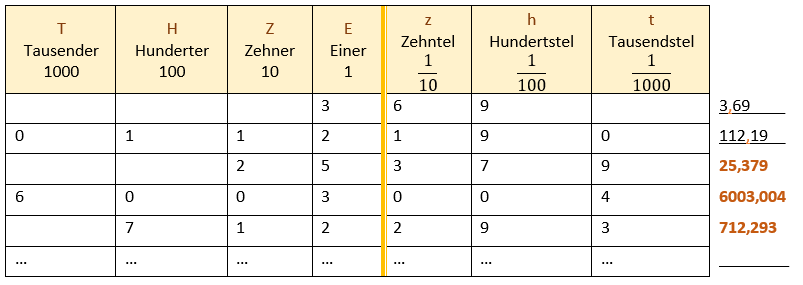
Tabelle 1

Vervollständige die Sätze mit drei Begriffen aus der Klammer und übernimm sie in dein Heft.

Das Komma steht immer zwischen und .
Die Stellen nach dem Komma heißen .

(Nachkommastellen, Tausender, Hunderter, Zehner, Einer, Zehntel)

Tom behauptet: „2,5 kann ich auch als 1E 15z (1 Einer 15 Zehntel) darstellen.“ Hat er recht?

Um dieser Frage auf den Grund zu gehen, nutzen wir die Darstellung der Zahlen mit Plättchen. Das kannst du am besten in der Stellenwerttafel-App machen. Gehe dazu auf diese Seite:
https://cinderella.de/files/ml215/stellenwerttafel.html

Durch Klicken fügst du ein Plättchen zur jeweiligen Spalte hinzu. Setze nun ein Plättchen in die Einer. Ziehe es dann in die Zehntel.
Beobachtung: 1E =10z.

Lösche nun die Plättchen wieder, setze ein neues in die Einer und ziehe es in die Hundertstel. Beobachtung: 1E = 10z = 100h.

Stelle jetzt 1E 15z dar. Stimmt Toms Behauptung?

Zurück zu Tom: Wie wir gesehen haben, hat er recht mit seiner Behauptung, dass 2,5 auch als 1E 15z dargestellt werden kann. Begründe nun mit deinen Beobachtungen aus den letzten Aufgaben, warum das so ist.
Schreibe die Begründung in dein Heft.

Das kannst du beobachten:

•Dezimalzahlen haben keine eindeutige Darstellung in der Stellenwerttafel.

•Zum Beispiel kann ein Einer (1E) auch als zehn Zehntel (10z) dargestellt werden.

•Die 15z kann man deswegen auch als 1E 5z schreiben.

•Damit entspricht die Zahl 1E 15z der Zahl 2,5.

Einheiten umrechnen

Wenn du Einheiten umrechnen möchtest, brauchst du die jeweiligen Umrechnungszahlen. Das sind die Zahlen, mit denen du multiplizieren bzw. dividieren musst, um von einer Einheit zur nächsten zu gelangen. Man kann diese Zahlen in folgenden Übersichten festhalten.

Übernimm die Grafiken in dein Heft. Fülle sie so weit wie möglich aus. Überlege dir dazu die Zusammenhänge aus deinem Alltag.
Verwende deinen Rechner zur Recherche, wenn du nicht weiterkommst. Such dafür nach Umrechnungszahlen Länge bzw. Masse. Du kannst auch Abkürzungen nachschlagen, die du nicht kennst.

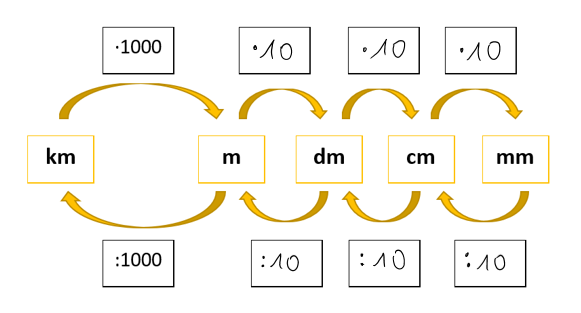
Umrechnungszahlen für die Länge

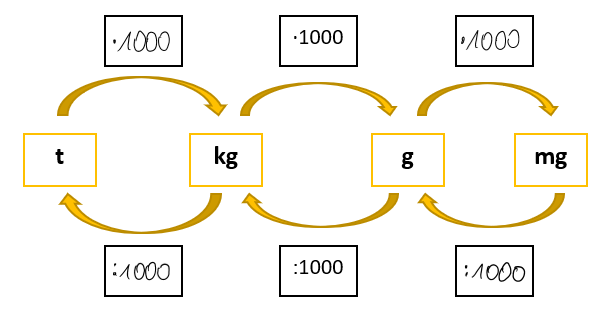
Umrechnungszahlen für die Masse

Löse die Aufgaben mit dem Umrechnungsschieber für Längen. Schreibe die Lösungen in dein Heft.

a) 45 cm = µm

b) 45 cm = m

c) 900 mm = dm = km

d) 3,215 m = cm

Löse die Aufgaben mit dem Umrechnungsschieber für Massen. Schreibe die Lösungen in dein Heft.

a) 4,2 t = kg

b) 305,8 g = kg

c) 52 mg = g

d) g = 15,372 kg

Löse die Aufgaben mit dem Umrechnungsschieber für Volumen. Schreibe die Lösungen in dein Heft.

a) 37,8 $d m^{3}$ = $c m^{3}$

b) 999 $m m^{3}$ = $c m^{3}$

c) 42,7 $m^{3}$ = $d m^{3}$

d) 0,003 $c m^{3}$ = $m m^{3}$