Positive und negative Zahlen in der Umwelt
Temperaturangaben
Höhenangaben in Landkarten (Meerestiefen)
Fahrstuhl (Tiefgarage)
Schulden auf dem Bankkonto
negative Spielstände (z.B. bei Ligretto)
....
Notiere die Etagen in deinem Hefter und überprüfe deine Ergebnisse mit deinem selbst gebastelten Fahrstuhl.
- Frau Müller fährt von Stockwerk 4 drei Stockwerke abwärts. → 1
- Herr Schneider fährt von Stockwerk -2 zwei Stockwerke abwärts. → -4
- Fatime fährt von Stockwerk 2 vier Stockwerke abwärts. → -2
- Thomas fährt von Stockwerk -2 fünf Stockwerke aufwärts. → 3
- Herr Gül ist in Stockwerk -3 und will ins Stockwerk -1. Wie viele Stockwerke muss er fahren? → 2 Stockwerke aufwärts
- Tonio ist in Stockwerk -2 und möchte ins Stockwerk 4. Wie viele Stockwerke muss er fahren? → 6 Stockwerke aufwärts

Einstieg
- 1
0
- 2
1
-2
- 4
2
Fahrt
- 3
+ 4
+ 5
- 3
+ 4
+4
-4
Ausstieg
- 4
4
3
- 2
2
0
-2
Rechnung
-1-3 = -4
0+4=4
-2+5=3
1-3=-2
-2+4=2
-4+4=0
2-4=-2
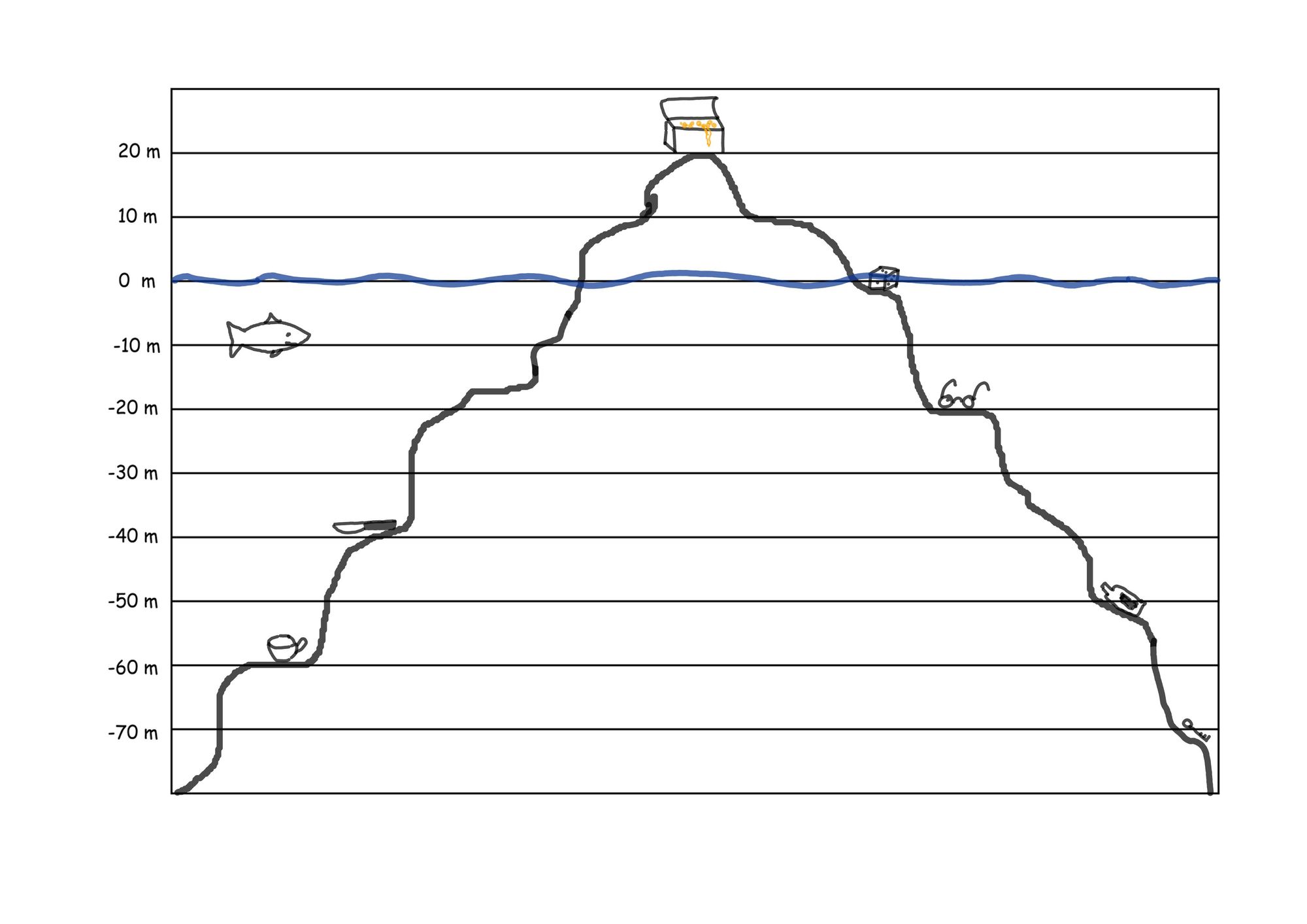
Messer: -40m, Tasse: -60 m, Würfel: 0m, Flasche: -50m, Schlüssel: -70m
https://editor.mnweg.org/entdecken/dokument/losungen-einfuhrung-negativer-zahlen
-3 °C
-4 °C
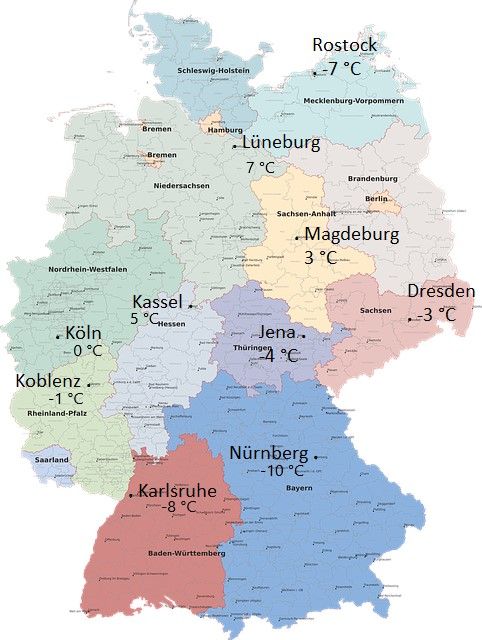
-7 °C
3 °C
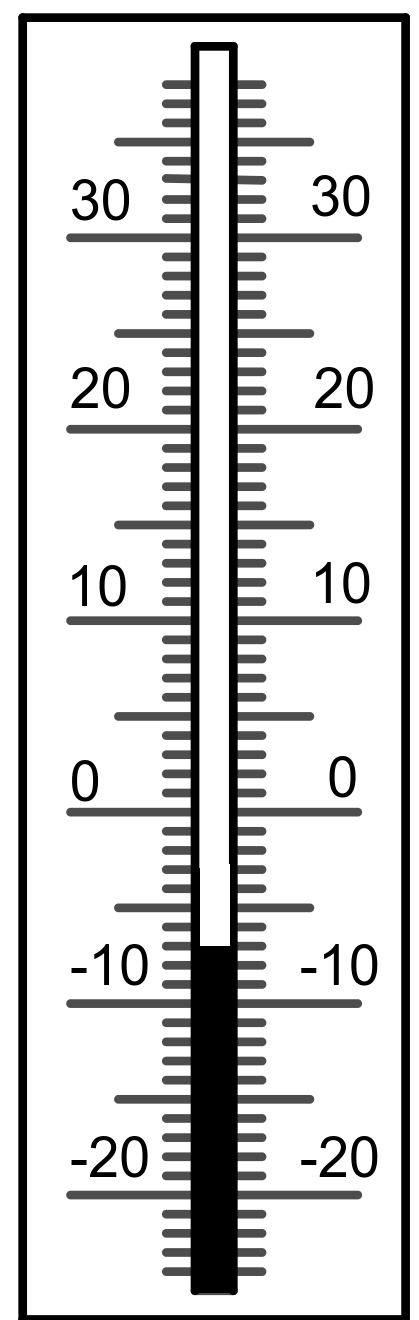
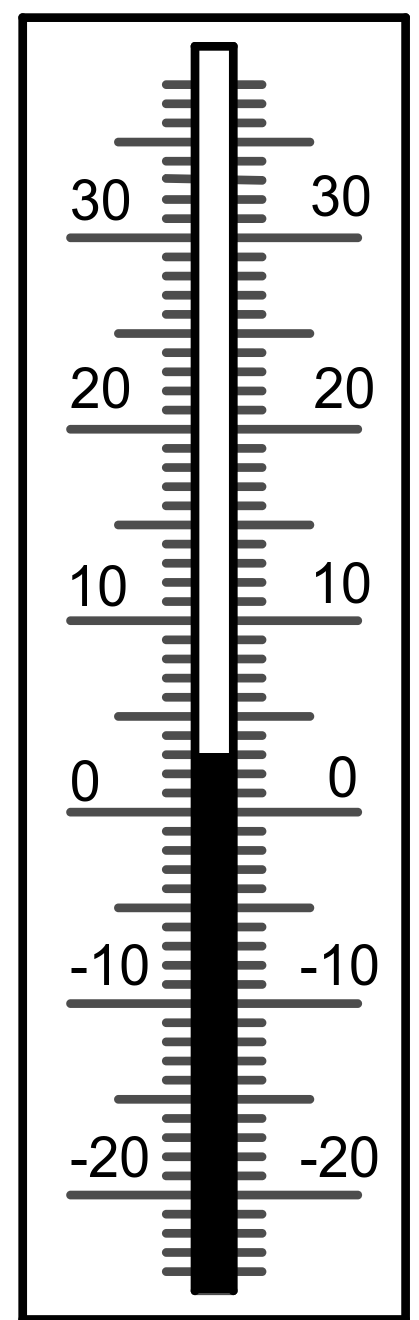
5 °C
0 °C
-1 °C
-8 °C
-10 °C
7 °C
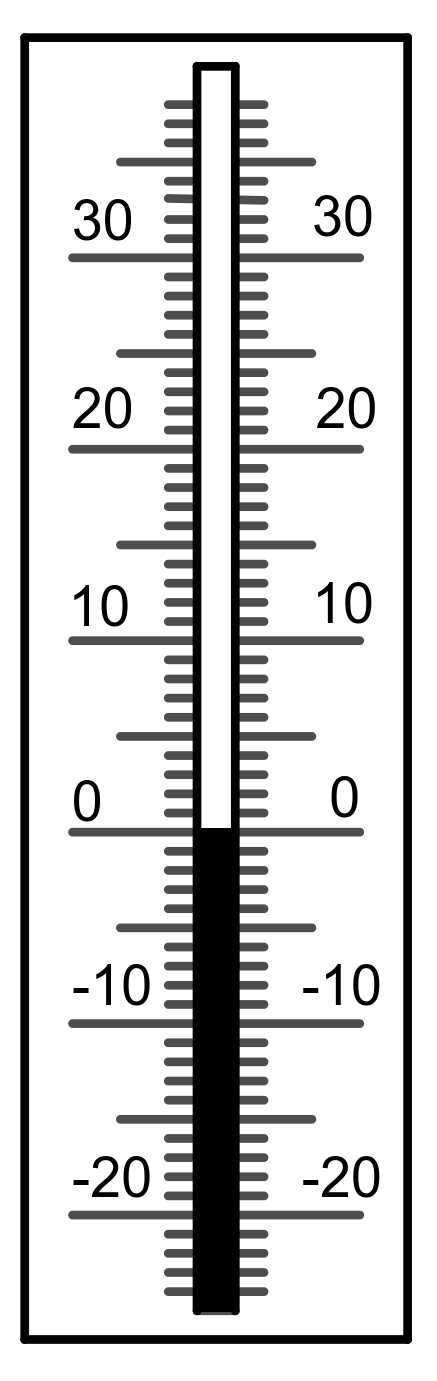
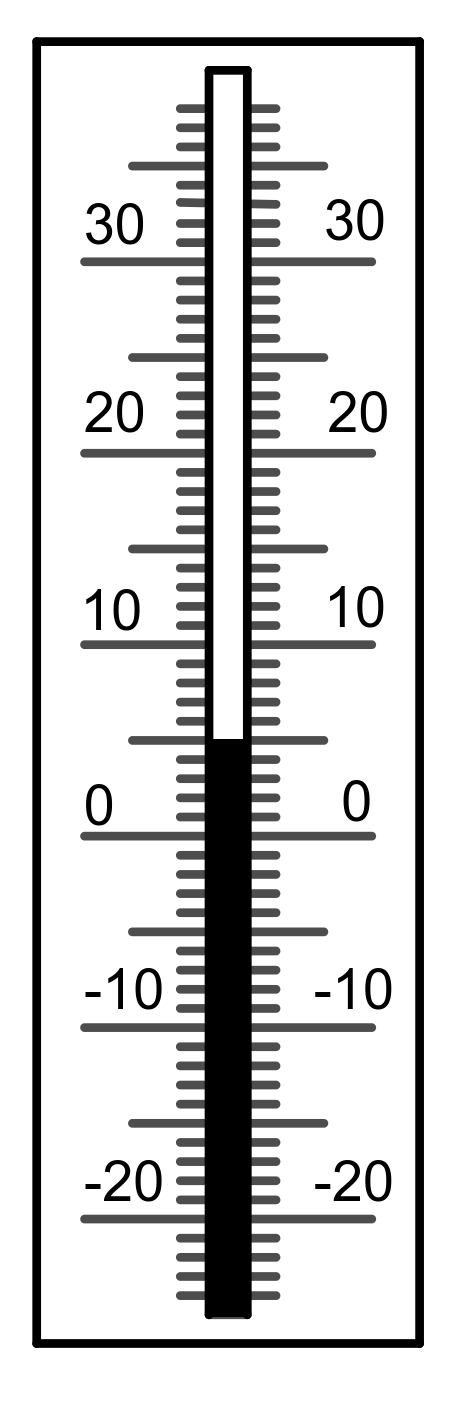
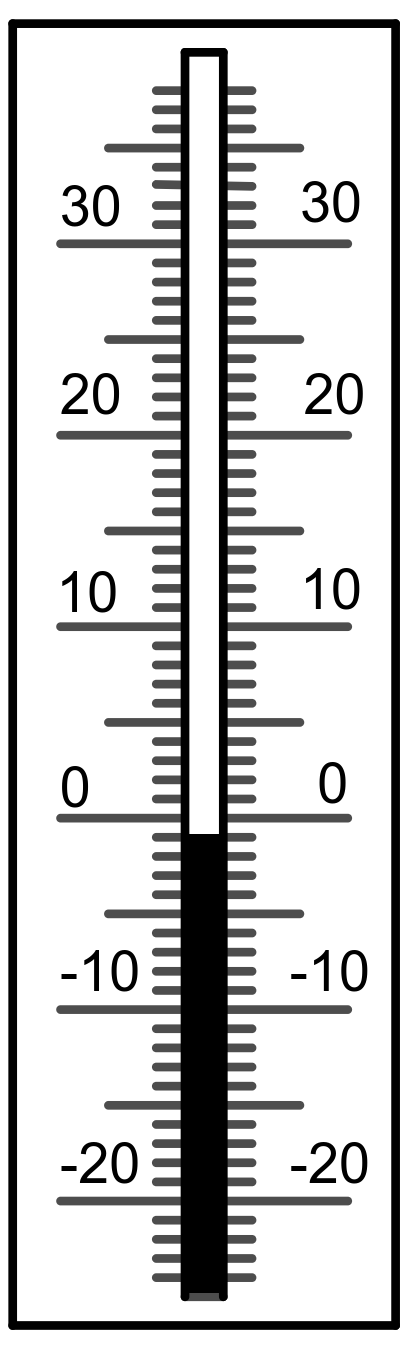
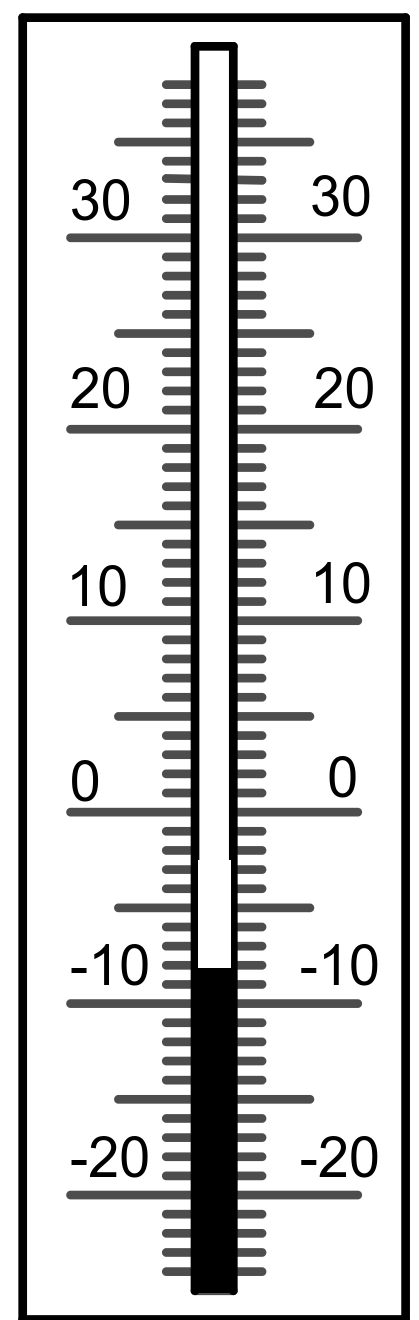
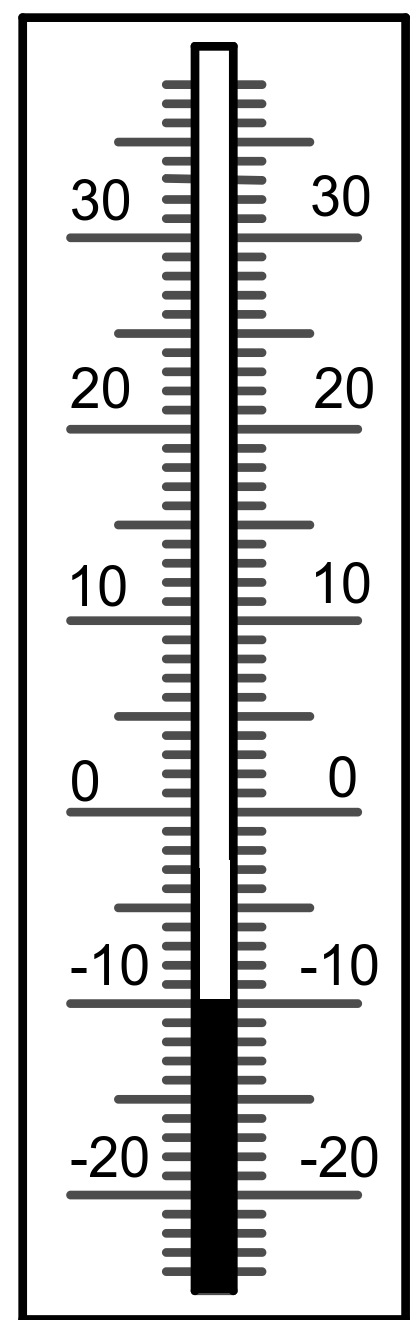
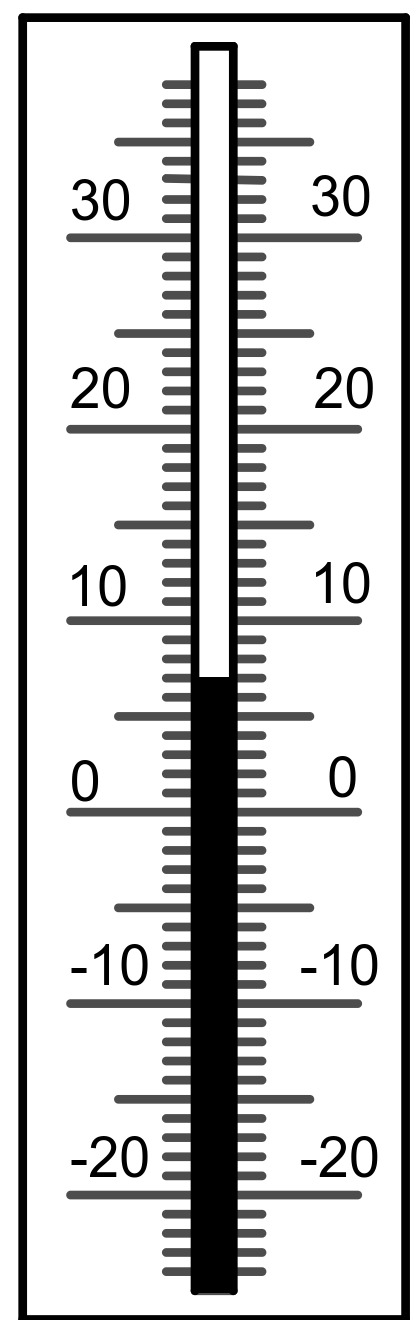
https://editor.mnweg.org/entdecken/dokument/losungen-einfuhrung-negativer-zahlen
Beginne mit der niedrigsten Temperatur und setze das richtige Relationszeichen.
- 0 - 5 = -5
0 > -5 - -5 + 3 = -2
-5 < - 2 - -3 + 4 = 1
-3 < 1
https://editor.mnweg.org/entdecken/dokument/losungen-einfuhrung-negativer-zahlen
Orientiere dich an der Zahlengerade.
| a) | 33 | 21 | |
| f) | 0 | −8 | |
| k) | −3 | −31 |
| b) | 33 | 6 | |
| g) | −15 | −15 | |
| l) | −21 | −25 |
| c) | −5 | 28 | |
| h) | −12 | 12 | |
| m) | −35 | 33 |
| d) | −33 | 3 | |
| i) | 11 | −29 | |
| n) | −22 | −6 |
| e) | 15 | −27 | |
| j) | −24 | 12 | |
| o) | −5 | 27 |
Orientieren kannst du dich an der Zahlengerade.
a) -20 < < < -10
b) -22 < < < -12
c) - 2 < < < 0
d) 0 < < < 12
e) -10 < < < 23
f) - 5 < < < - 3,5
a = - 2,5; b = - 5,7; c = - 4,3; d = - 3,3; e = - 1,7; f = 3,1; g = 2,6; h = 5,8
b und c:
e und f:
g und h:
b und d:
https://editor.mnweg.org/entdecken/dokument/losungen-einfuhrung-negativer-zahlen
Das Koordinatensystem - Wiederholung
Ein Koordinatensystem besteht aus zwei mit gemeinsamem Anfangspunkt, die als Achse und Achse bezeichnet werden.
Die und die stehen immer zueinander.
Ein im Koordinatensystem kann mit einem Zahlenpaar (x; y) beschrieben werden.
Die erste Koordinate ist der -Wert und die zweite Koordinate der -Wert eines Punktes.
Der Punkt O=(0; 0) heißt .
Koordinatenursprung, Zahlenstrahlen, x-, y-, Punkt, x, y, x-Achse, senkrecht, y-Achse y-Achse
https://editor.mnweg.org/entdecken/dokument/losungen-einfuhrung-negativer-zahlen
Das vollständige Koordinatensystem
A ( ; )
B ( ; )
C ( ; )
D ( ; )
Ergänze die Koordinaten der Punkte A'B'C'D'E'F'G'. Wenn du möchtest, kannst du die entstehende Figur farbig gestalten.
A' ( ; )
B' ( ; )
C' ( ; )
D' ( ; )
E'( ; )
F' ( ; )
G' ( ; )
https://editor.mnweg.org/entdecken/dokument/losungen-einfuhrung-negativer-zahlen
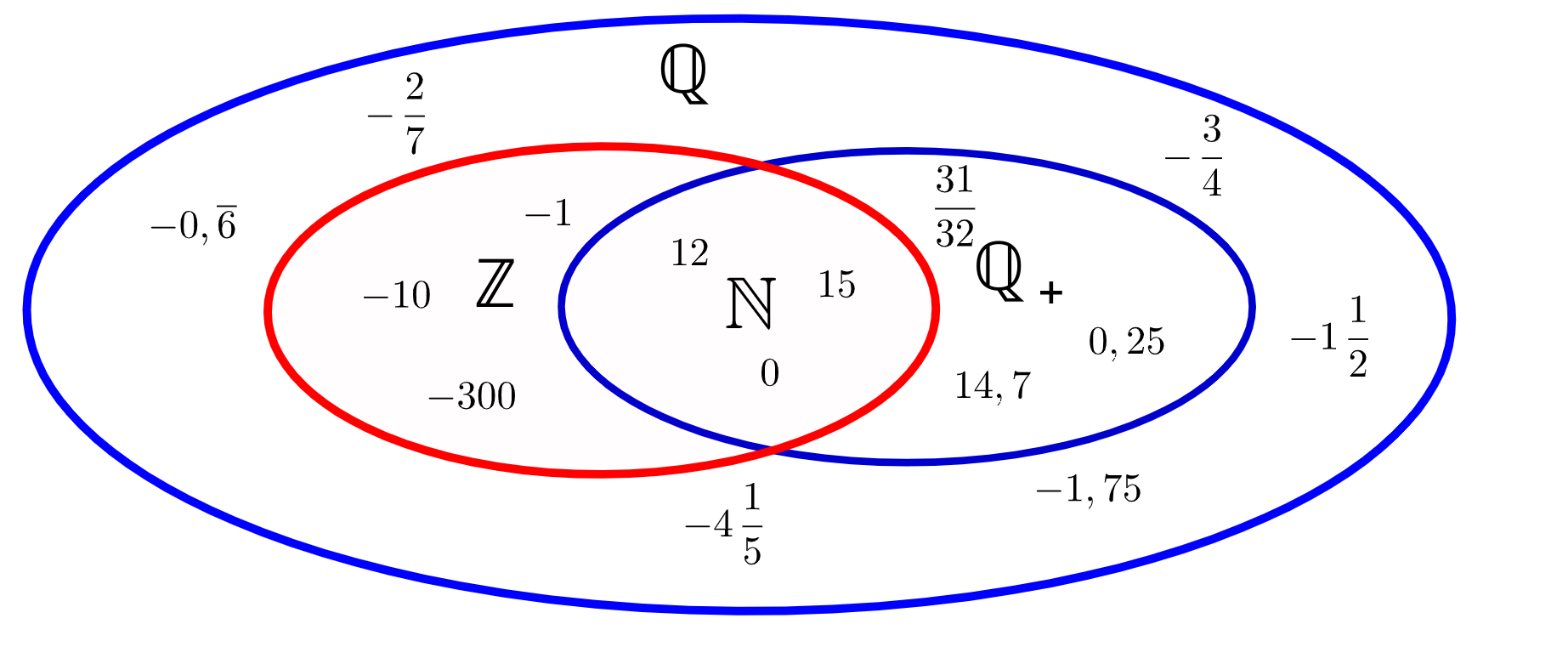
Zahl
−23
0,3
−22,5
−331
53
57
41
-41
0
−8
ℕ
x
x
ℤ
x
x
x
x
ℚ+
x
x
x
x
x
ℚ
x
x
x
x
x
x
x
x
x
x
https://editor.mnweg.org/entdecken/dokument/losungen-einfuhrung-negativer-zahlen


