Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
Bei der Untersuchung von linearen Funktionen interessiert man sich oftmals für den Schnittpunkt mit der x-Achse.
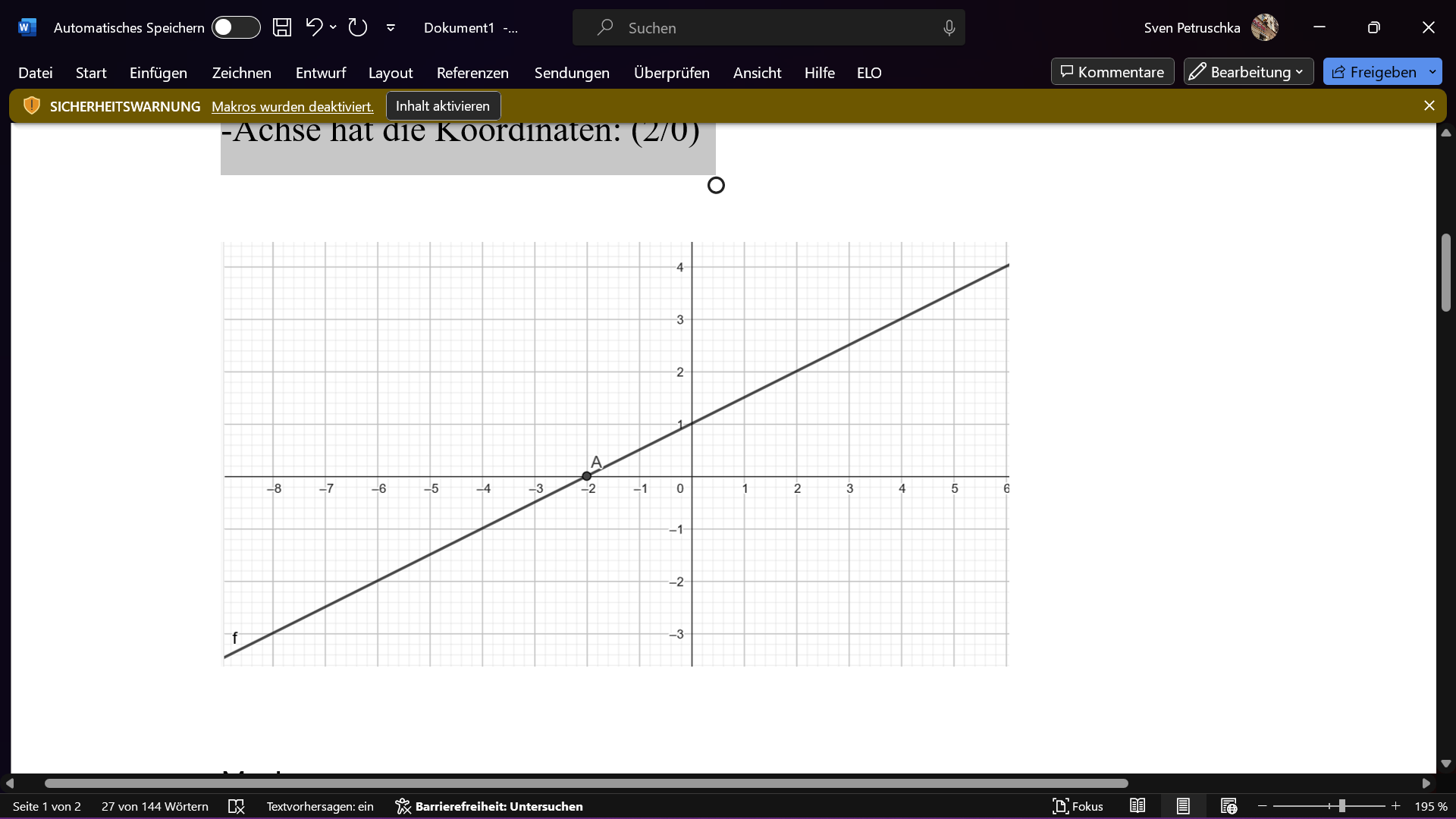
In der Abbildung ist der Graph einer linearen Funktion eingezeichnet. Sein Schnittpunkt mit der x-Achse ist der Punkt A.
Der Schnittpunkt mit der x-Achse hat die Koordinaten: (2/0)
Nullstelle
Merke
Die Nullstelle ist die x-Koordinate des Schnittpunkts des Graphen mit der x-Achse.
Die Nullstelle einer linearen Funktion erhält man, indem man y = 0 setzt, also die Lösung der Gleichung 0 = ax + b bestimmt.
Rechenweg
Beispiel:
y = 0,5x + 1
0 = 0,5x + 1 /-1
-1 = 0,5x /:0,5
-2 = x
Nullstelle: (-2/0)
