Kern­bin­dungs­en­er­gie und Mas­sen­de­fekt

Be­stimmt man die Masse eines Atom­kerns, wel­cher aus Z Pro­to­nen und N Neu­tro­nen be­steht und ver­gleicht dies mit der Summe der Masse der Be­stand­tei­le, so stellt man fest, dass der Kern leich­ter als seine Be­stand­tei­le ist. Am ein­fachs­ten kann man dies am He­li­um­kern nach­rech­nen, die zwei Pro­to­nen und die zwei Neu­tro­nen sind um $0,0504\cdot 10^{-27}$kg schwe­rer als der He­li­um­kern.

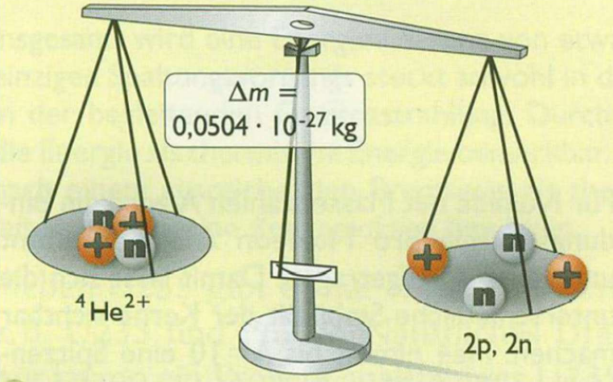
Die feh­len­de Masse steckt in der star­ken Kern­kraft, sie wirkt als an­zie­hen­de En­er­gie dem Aus­ein­an­der­flie­gen der Teil­chen ent­ge­gen und wird daher auch (Kern-)Bin­dungs­en­er­gie ge­nannt. Der Wert der feh­len­den Masse wird Mas­sen­de­fekt ge­nannt. Man kann den Be­trag der En­er­gie aus dem Mas­sen­de­fekt über die be­kann­te Einstein-​Gleichung E=mc² be­rech­nen.

Um die Bin­dungs­en­er­gien der ver­schie­de­nen Atom­ker­ne mit­ein­an­der ver­glei­chen zu kön­nen,

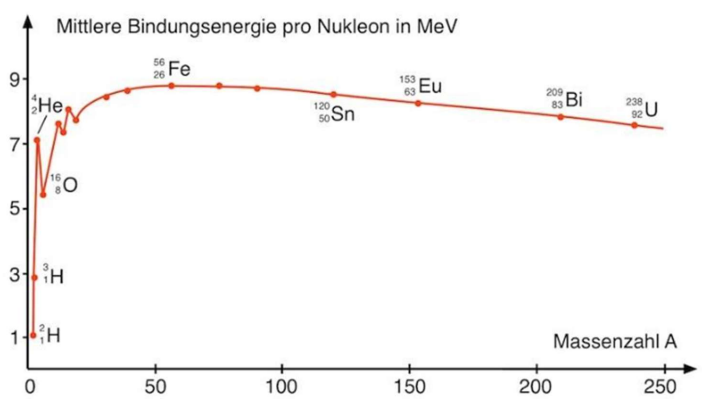
be­stimmt man die mitt­le­re Bin­dungs­en­er­gie pro Nu­kle­on, also pro Kern­teil­chen, beim He­li­um

sind dies ca. 7 MeV. In dem Dia­gramm sind die Bin­dungs­en­er­gien pro Nu­kle­on über der Mas­sen­zahl auf­ge­tra­gen.