Willkommen im Baustein Multiplikation und Division mit Zehnerpotenzen

Nach diesem Baustein...

...kannst du Dezimalzahlen in die Stellenwerttafel eintragen und aus ihr ablesen.

...kennst du den Begriff der Zehnerpotenz.

...kannst du Dezimalzahlen mit Zehnerpotenzen multiplizieren und dividieren.

...kannst du Einheiten für Längen, Massen und Volumen umrechnen.

Step 1

Dezimalzahlen in der Stellenwerttafel

Step 2

Multiplikation und Division mit Zehnerpotenzen

Step 3

Umrechnen von Einheiten

Vorwissen

Kennst du dich noch mit Dezimalzahlen aus?

Dezimalzahlen in der Stellenwerttafel

Im Alltag begegnen uns immer wieder Dezimalzahlen

Beispiele für Dezimalzahlen

1

Finde weitere Beispiele für Dezimalzahlen in deiner Umwelt. Male oder schreibe sie in dein Heft. Du kannst auch Dinge aufkleben.

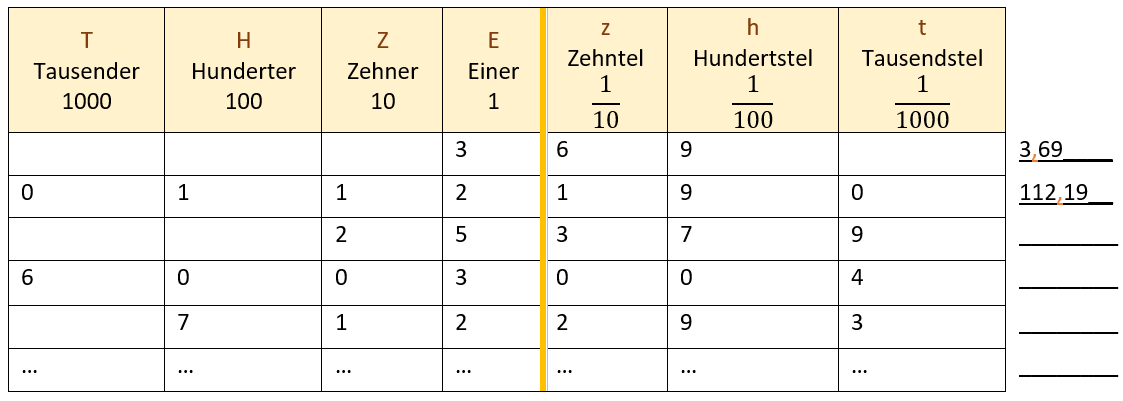
Um Dezimalzahlen übersichtlich darzustellen, nutzt man die Stellenwerttafel, die du bereits für natürliche Zahlen kennst. Für Dezimalzahlen erweitern wir die Stellenwerttafel nach rechts. Dabei kommen zuerst die Zehntel, dann die Hundertstel, Tausendstel und so weiter.

Tabelle 1

2

Übernimm die Tabelle 1 in dein Heft. Ergänze rechts die fehlenden Dezimalzahlen. Trage nun noch mindestens vier deiner gefundenen Zahlen aus Aufgabe 1 ein.

weitere Übung

In der Anton-App kannst du noch weiter mit der Stellenwerttafel üben:

Mathematik 6. Klasse - Dezimalzahlen kennenlernen - Dezimalzahlen schreiben (1)

3

Vervollständige die Sätze mit drei Begriffen aus der Klammer und übernimm sie in dein Heft.

Das Komma steht immer zwischen und .
Die Stellen nach dem Komma heißen .

(Nachkommastellen, Tausender, Hunderter, Zehner, Einer, Zehntel)

Schreibweise

Wir können auch schreiben:

23,671 = 2 Zehner, 3 Einer, 6 Zehntel, 7 Hundertstel und 1 Tausendstel = 2Z 3E 6z 7h 1t

4

Übe diese neue Schreibweise in der Anton-App.
Mathematik 6. Klasse - Dezimalzahlen kennenlernen - Dezimalzahlen zuordnen

5

Tom behauptet: „2,5 kann ich auch als 1E 15z (1 Einer 15 Zehntel) darstellen.“ Hat er recht?

Um dieser Frage auf den Grund zu gehen, nutzen wir die Darstellung der Zahlen mit Plättchen. Das kannst du am besten in der Stellenwerttafel-App machen. Gehe dazu auf diese Seite:
https://cinderella.de/files/ml215/stellenwerttafel.html

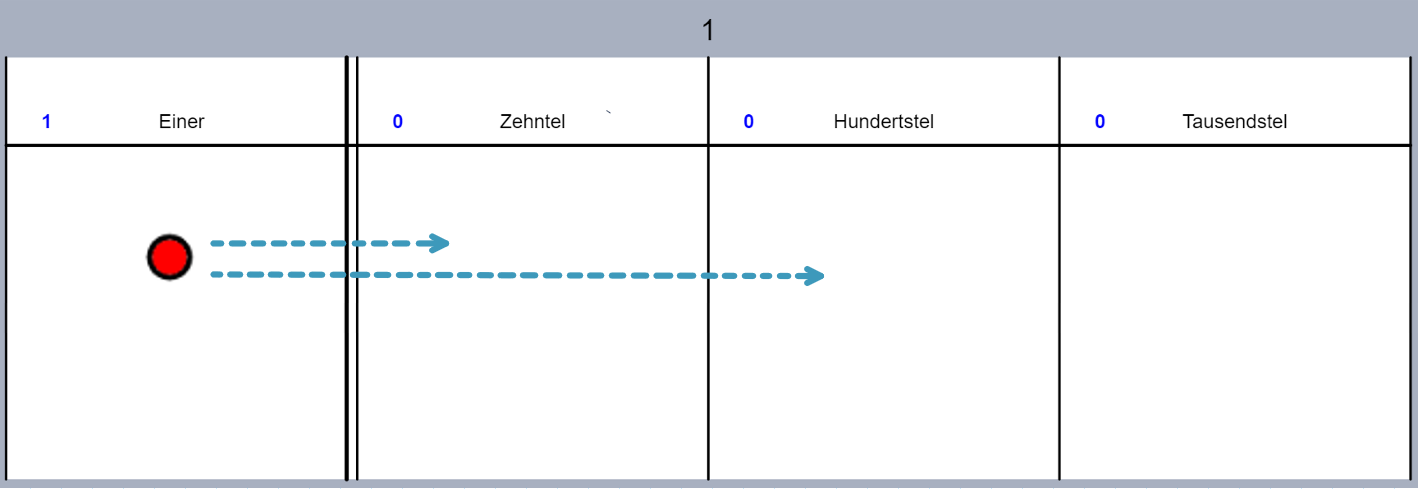
Durch Klicken fügst du ein Plättchen zu einer Spalte hinzu. Setze nun ein Plättchen in die Einer. Ziehe es dann in die Zehntel. Beobachtung: 1E =.......z.

Lösche nun die Plättchen wieder, setze ein neues in die Einer und ziehe es in die Hundertstel. Beobachtung: 1E = ......z = .......h.

Stelle jetzt 1E 15z dar. Stimmt Toms Behauptung?

Ansicht in der App

Übung und Vertiefung

Löse die Aufgaben auf dem Arbeitsblatt "Vertiefung der Stellenwerttafel und Übungen". Das Blatt findest du bei den Kopiervorlagen.

6

Zurück zu Tom: Wie wir gesehen haben, hat er recht mit seiner Behauptung, dass 2,5 auch als 1E 15z dargestellt werden kann. Begründe nun mit deinen Beobachtungen aus den letzten Aufgaben, warum das so ist.
Schreibe die Begründung in dein Heft.

Multiplikation und Division mit 10, 100, 1000 ...

Lernziel

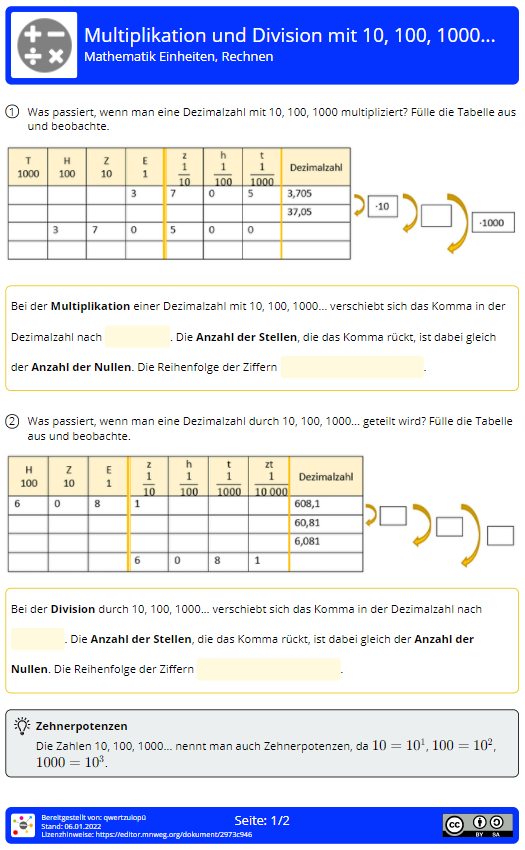
Nach diesem Abschnitt kannst du beliebige Dezimalzahlen mit Zehnerpotenzen wie 10, 100, 1000... multiplizieren und dividieren. Bearbeite dazu das Arbeitsblatt aus den Kopiervorlagen.

Achtung! Das Blatt hat zwei Seiten.

Einheiten umrechnen

Bisher hast du dich mit der Stellenwerttafel und der Multiplikation und Division mit Zehnerpotenzen beschäftigt. Im folgenden Abschnitt wirst du dieses Wissen nutzen, um Einheiten umzurechnen.

Einheiten

In Deutschland benutzen wir Einheiten wie Meter und Kilogramm. Diese Maße sind praktisch, weil man sie leicht umrechnen kann. So sind zum Beispiel

•1 000 m = 1 km

•1 000 g = 1 kg

Die USA verwenden z.B. ein anderes System, in dem die Umrechnung nicht so einfach ist:

•1 Meile = 1760 Yards (Länge)

•1 Pfund = 16 Unzen (Masse)

Wenn du Einheiten sicher umrechnen kannst, kannst du zum Beispiel Fragen wie diese beantworten:

Ich brauche 800g Mehl zum Backen. Ich habe aber nur eine 1kg-Tüte im Schrank. Reicht das?
Die Bushaltestelle Am Rathaus ist 850 m von Tims Haustür entfernt. Zur Haltestelle Hauptstraße läuft er 0,6 km. Welche liegt näher?"

1

Wenn du Einheiten umrechnen möchtest, brauchst du die jeweiligen Umrechnungszahlen. Das sind die Zahlen, mit denen du multiplizieren bzw. dividieren musst, um von einer Einheit zur nächsten zu gelangen. Man kann diese Zahlen in folgenden Übersichten festhalten.

Übernimm die Grafiken in dein Heft. Fülle sie so weit wie möglich aus. Überlege dir dazu die Zusammenhänge aus deinem Alltag.
Verwende deinen Rechner zur Recherche, wenn du nicht weiterkommst. Such dafür nach Umrechnungszahlen Länge bzw. Masse. Du kannst auch Abkürzungen nachschlagen, die du nicht kennst.

Umrechnungszahlen der Länge

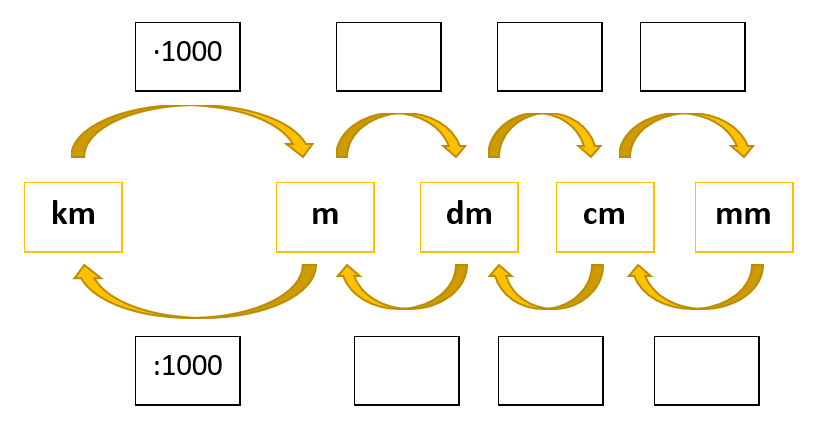
Umrechnungszahlen der Masse

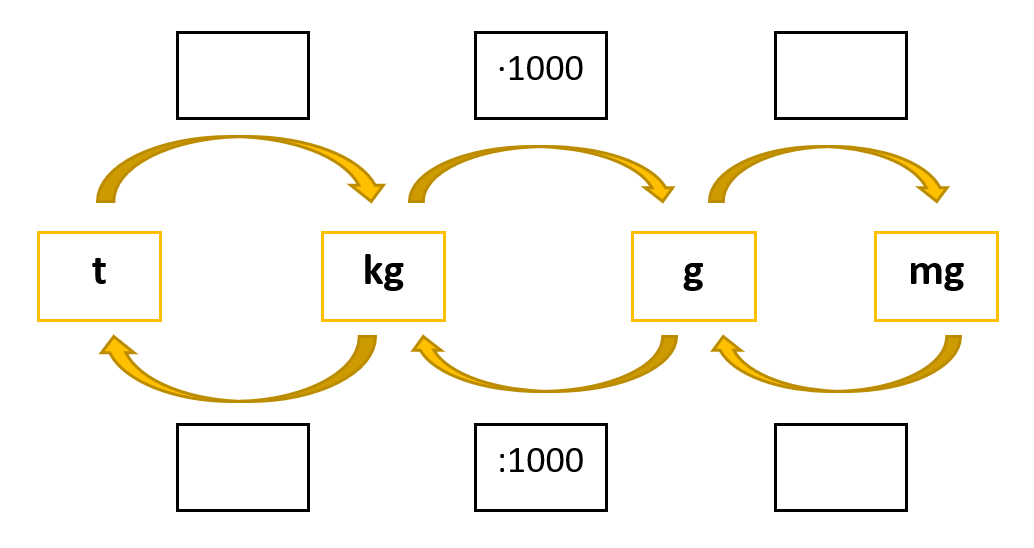
Zum Beispiel ist

5 km = 1000 · 5 m = 5000 m
3 cm = 3 : 10 dm = 0,3 dm
4 kg = 4 · 1000 g = 4000 g
50 mg = 50 : 1000 g = 0,05 g

Umrechnungsschieber

Wir können einen sogenannten Umrechnungsschieber benutzen, um Einheiten schnell umzurechnen. Du findest diese Schieber für verschiedene Einheiten im Material zu diesem Baustein.

Anleitung für die Umrechnungsschieber

In der Kopfzeile sind die Einheiten bereits passend eingetragen.
Wenn du eine Zahl umrechnen willst, trage sie nach ihren Stellenwerten in die Tabelle ein. Der Einer steht dabei unter der gegebenen Einheit.
Lege nun deinen Stift als "Komma" rechts neben die Einheit, in die du umrechnen möchtest.
Leere Kästchen entsprechen einer 0.
Also zum Beispiel: 245 cm = 2450 mm= 24,5 dm

Achtung

Verwende auf den laminierten Umrechnungsschiebern ausschließlich die dazugehörenden Folienstifte.

Umrechnung von Längen

In der Verteilung der Einheiten in der Kopfzeile findest du die Umrechnungszahlen wieder.
Im Beispiel kann man erkennen: 1500 m = 1,5 km

2

Löse die Aufgaben mit dem Umrechnungsschieber für Längen. Schreibe die Lösungen in dein Heft.

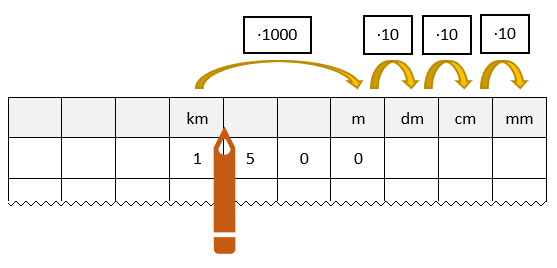
a) 45 cm = µm

b) 45 cm = m

c) 900 mm = dm = km

d) 3,215 m = cm

Umrechnung von Massen

Auch hier findest du die Umrechnungszahlen von vorhin wieder.
Das Beispiel bedeutet: 3,875 kg = 3875 g

3

Löse die Aufgaben mit dem Umrechnungsschieber für Massen. Schreibe die Lösungen in dein Heft.

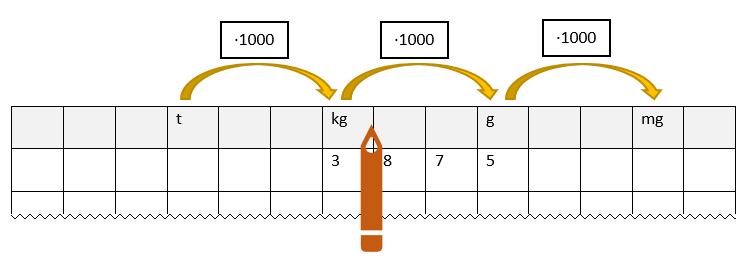
a) 4,2 t = kg

b) 305,8 g = kg

c) 52 mg = g

d) g = 15,372 kg

Umrechnung von Volumen

Hier kann man zum Beispiel ablesen: $14550 c m^{3} = 14, 55 d m^{3}$

Volumen

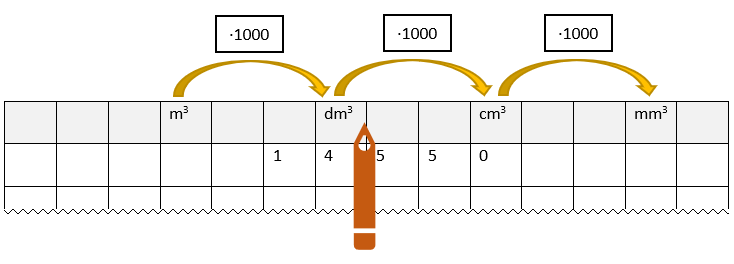
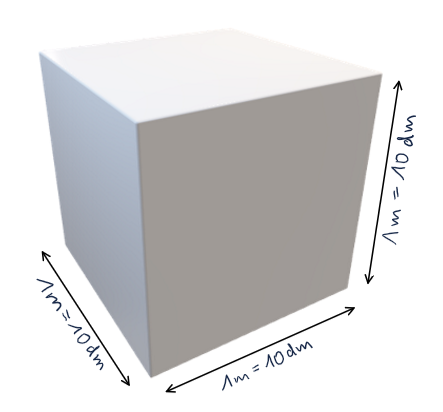
Wegen der 3 Dimensionen sind die Umrechnungszahlen für Volumeneinheiten gleich

$10 \cdot 10 \cdot 10 = 1 0^{3} = 1000$

Mehr dazu findet ihr im Baustein zu Volumen.

4

Löse die Aufgaben mit dem Umrechnungsschieber für Volumen. Schreibe die Lösungen in dein Heft.

a) 37,8 $d m^{3}$ = $c m^{3}$

b) 999 $m m^{3}$ = $c m^{3}$

c) 42,7 $m^{3}$ = $d m^{3}$

d) 0,003 $c m^{3}$ = $m m^{3}$

Freiwillige Übung

Wenn du noch weiter üben willst, dann löse die Aufgaben in der Anton-App. Nutze dazu den Umrechnungsschieber, wenn du ihn brauchst.

Länge

Masse

Volumen

Mathematik Klasse 5 - Rechnen mit Volumeneinheiten - Einheiten umwandeln gemischt

Mathematik Klasse 5 - Rechnen mit Gewichten - Gewichte umrechnen (2)

Mathematik Klasse 5 - Rechnen mit Längen - Größenangaben umwandeln (2)

Geschafft!

Du kannst jetzt...

...Dezimalzahlen in die Stellenwerttafel eintragen und aus ihr ablesen.

...den Begriff "Zehnerpotenzen" benutzen.

...Dezimalzahlen mit Zehnerpotenzen multiplizieren und dividieren.

...Einheiten für Längen, Massen und Volumen umrechnen.

Quellen

Jenert, E. / Kühne, P. (2018): Klick! inklusiv: Mathematik, Arbeitsheft, 7/8.
Hoffkamp A. / Podemski J.: Friedrich Verlag GmbH | mathematik lehren 215 | 2019.
Schroedel Verlag GmbH, 2001, Arbeitsblatt: Dezimalbruch mal und geteilt durch 10, 100, 1000, ...

Hinweis zum Einsatz im Unterricht

Willkommen im Baustein Multiplikation und Division mit Zehnerpotenzen

Vorwissen

Dezimalzahlen in der Stellenwerttafel

Multiplikation und Division mit 10, 100, 1000 ...

Einheiten umrechnen

Umrechnungsschieber

Umrechnung von Längen

Umrechnung von Massen

Umrechnung von Volumen

Freiwillige Übung

Quellen