TitelNormalform
Autoranonym
veröffentlicht28.10.2025
FachMathematik
KompetenzbereichFunktionen
NiveaustufenM (Mindeststandard), R (Regelstandard)
Phase9
MaterialformInputmaterial

Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

In diesem Kapitel stellen sich die Parameter der Normalform quadratischer Funktionen vor. Du kannst herausfinden,

wie man Parabeln strecken, stauchen und spiegeln kann,
welchen Einfluss die Parameter der Normalform auf das Aussehen und die Lage der Parabel haben und
wie du das an den Funktionstermen erkennen kannst.

Strecken, Stauchen, Spiegeln: $y = a x^{2}$

Du weißt bereits, was passiert, wenn man statt der Funktion $y = x^{2}$ folgende Funktionen gegeben hat:

$y = 2 x^{2}$
$y = \frac{1}{2} x^{2}$
$y = - x^{2}$

Hier nur nochmal zur Erinnerung:

Merke

Multipliziert man $y = x^{2}$ mit einem Faktor a, wird die Parabel gestreckt, gestaucht und/oder gespiegelt. $y = a x^{2}$ (mit a≠0) ergibt demnach für:

a > 0: Die Parabel ist nach oben geöffnet.

a < 0: Die Parabel ist nach unten geöffnet.

|a| > 1: Die Parabel ist gestreckt

|a| < 1: Die Parabel ist gestaucht

Der Parameter a wird auch Streckungsfaktor genannt.

Der Parameter b bei $y = x^{2} + b x$

Was passiert, wenn man statt der Funktion $y = x^{2}$ folgende Funktionen gegeben hat:

$y = x^{2} + 3 x$
$y = x^{2} - 3 x$

Notiere Vermutungen darüber, wie die Graphen der Funktionen (1) und (2) aussehen, ohne diese zu zeichnen.

Öffne anschließend das GeoGebra Applet und versuche, deine Vermutungen zu überprüfen, indem du nur den Parameter b veränderst.

Hinweis

Wenn du dir unsicher bei der Formulierung deiner Vermutungen bist, kannst du Wertetabellen für die zwei Funktionen aufstellen und die Funktionswerte mit den Werten von $y = x^{2}$ vergleichen.

Tipp

Wie sieht der Graph aus: Ist er nach oben oder nach unten geöffnet? Nach rechts oder nach links verschoben?

Wende dein Wissen über die Parameter a und b an.

Spiele anschließend das folgende Spiel:

Merke

Addiert man den Ausdruck $b x$ zu $y = a x^{2}$ , wird die Parabel sowohl in x- als auch in y-Richtung verschoben. Für $y = a x^{2} + b x$ gilt:

Für a>0:

b>0: Die Parabel wird nach links und unten verschoben.

b<0: Die Parabel wird nach rechts und unten verschoben.

Für a<0:

b>0: Die Parabel wird nach rechts und oben verschoben.

b<0: Die Parabel wird nach links und oben verschoben.

Der Parameter c bei $y = a x^{2} + b x + c$

Was passiert, wenn man statt der Funktion $y = x^{2}$ folgende Funktionen gegeben hat:

$y = x^{2} + 3 x + 2$
$y = x^{2} + 3 x - 2$

Hinweis

Wenn du dir unsicher bei der Formulierung deiner Vermutungen bist, kannst du Wertetabellen für die zwei Funktionen aufstellen und die Funktionswerte mit den Werten von $y = x^{2}$ vergleichen.

Notiere Vermutungen darüber, wie die Graphen der Funktionen (1) und (2) aussehen, ohne diese zu zeichnen.

Öffne anschließend das GeoGebra Applet und versuche, deine Vermutungen zu überprüfen, indem du nur den Parameter c veränderst.

Spiele anschließend das folgende Spiel:

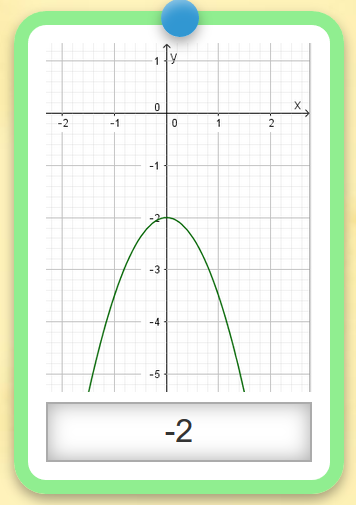
Beispiel: Welchen Wert hat der Parameter c? Trage deine Lösung wie in dem Beispiel ein:

Merke

Der Parameter c bewirkt eine Verschiebung der Parabel in y-Richtung. Er gibt dabei den y-Achsenabschnitt der Parabel $y = a x^{2} + b x + c$ an. Es gilt für:

c>0: Die Parabel wird in positive y-Richtung (nach oben) verschoben.

c<0: Die Parabel wird in negative y-Richtung (nach unten) verschoben.

Merke

Die auf dieser Seite gewonnen Erkenntnisse können kombiniert werden und ergeben quadratische Funktion der Form $y = a x^{2} + b x + c$ . Diese Form heißt Normalform.

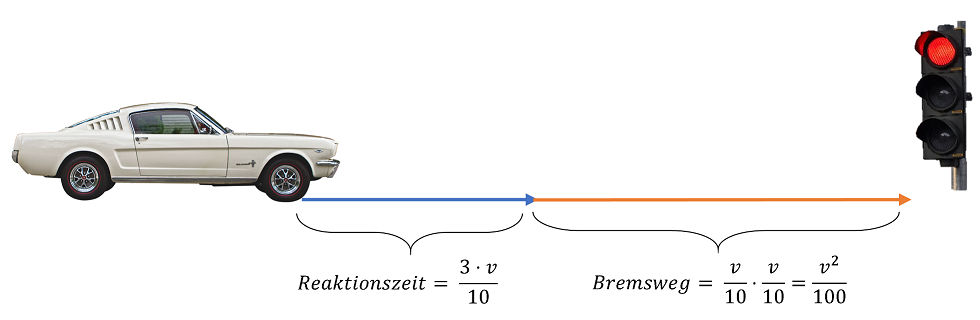
In der Fahrschule lernt man eine Faustformel zur Berechnung des Bremsweges eines Autos kennen. Sie lautet „Geschwindigkeit durch 10 Mal Geschwindigkeit durch 10“ – in Termen ausgedrückt (mit v für Geschwindigkeit):

$f (v) \approx \frac{v}{10} \cdot \frac{v}{10}$

Für den tatsächlichen Anhalteweg muss jedoch auch noch der Reaktionsweg des Fahrers beachtet werden. Durch ihn wird ein Weg von annähernd „drei Mal die Geschwindigkeit durch 10“ zurückgelegt und der zugehörige Term lautet:

$f (v) \approx \frac{3 \cdot v}{10}$

Kombiniert man Bremsweg und Reaktionsweg, so lässt sich näherungsweies der Anhalteweg eines PKW bestimmen. Die zusammengesetzte Formel lautet:

$f (v) \approx \frac{v}{10} \cdot \frac{v}{10} + \frac{3 \cdot v}{10} = \frac{v ^{2}}{100} + \frac{3 \cdot v}{10}$

Berechne den Anhalteweg für die Geschwindigkeiten: 30 km/h, 50 km/h und 70 km/h und 100 km/h. Zur Kontrolle kannst du das folgende Applet benutzen und die Lösungen:

Merke

Terme quadratischer Funktionen können in der Form $f (x) = a x^{2} + b x + c$ (mit $a \neq = 0$ ) beschrieben werden. Diese Darstellungsform nennt man Normalform. In der Normalform quadratischer Funktionen kann der y-Achsenabschnitt c direkt abgelesen werden.

Das folgende Quiz beschäftigt sich mit dem Wechsel zwischen verschiedenen Darstellungsarten (Funktionsterm, Graph und Tabelle) quadratischer Funktionen. Löse das folgende Quiz, indem du immer zwei Karten zu einem Paar zusammenfügst.

Hinweis

Du kannst...

...den y-Achsenabschnitt an den Funktionsgraphen ablesen. Passt er zu einem der Funktionsterme? Oder findest du ihn in einer der Tabellen wieder?

...einen beliebigen Punkt an den Graphen ablesen. Setze die Koordinaten in einen der Funktionsterme ein oder vergleiche sie mit den Werten in einer der Tabellen.

...im Abschnitt Parameter nachschauen wofür die Paramter in der Normalform stehen. Was ist nochmal der y-Achsenabschnitt, was der Streckungsfaktor?

Stre­cken, Stau­chen, Spie­geln: ﻿y=ax2

Der Pa­ra­me­ter ﻿b bei ﻿y=x2+bx

Der Pa­ra­me­ter ﻿﻿c﻿﻿ bei ﻿y=ax2+bx+c

Strecken, Stauchen, Spiegeln: $y = a x^{2}$

Der Parameter b bei $y = x^{2} + b x$

Der Parameter c bei $y = a x^{2} + b x + c$