HerunterladenAls PDF Herunterladen
  • Nullstellen quadratischer Funktionen
  • anonym
  • 07.10.2025
  • Mathematik
  • Funktionen
  • R (Regelstandard)
  • 9
  • Inputmaterial
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
Input
Nullstellen quadratischer Funktionen
Mathematik Funktionen R 9
Null­stel­le

Die Stel­le, an der ein Graph die x-​Achse schnei­det oder be­rührt, nennt man Null­stel­le.

An­ge­ge­ben wird dann die x-​Koordinate.

1
An wel­cher Stel­le schnei­det der Graph die x-​Achse? Gib die Ko­or­di­na­te an:

Da dort, wo die x-​Achse ge­schnit­ten wird, der zu­ge­hö­ri­ge y-Wert  be­trägt, schreibt man die Null­stel­le manch­mal auch in Form eines Punk­tes:
 
Der Punkt hat dann auf jeden Fall die y-​Koordinate . Man ver­wen­det dann meis­tens die Ab­kür­zung  für Null­stel­le für den Punkt.
123x123yoriginO
f(x)
123x123yoriginO
f(x)
−2−112x123456789yoriginO−2−112x123456789yoriginO
2
Be­trach­te den Gra­phen der Nor­mal­pa­ra­bel .
  • Gib die Null­stel­le in bei­den Dar­stel­lungs­for­men an:
      und  
  • Was ist hier der rich­ti­ge Be­griff aus Dei­ner Sicht?
    ( ) der Graph schnei­det die x-​Achse
    ( ) der Graph be­rührt die x-​Achse
Bereitgestellt von: anonym Stand: 07.10.2025 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/nullstellen-quadratischer-funktionen-tx7whvrq
Seite: 1/3
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/nullstellen-quadratischer-funktionen-tx7whvrq
Input
Nullstellen quadratischer Funktionen
Mathematik Funktionen R 9
Be­rüh­ren oder schnei­den

Man sagt der Graph be­rührt die x-​Achse, wenn er in einer klei­nen Um­ge­bung links und rechts der Null­stel­le ober­halb der x-​Achse ver­läuft (oder un­ter­halb).

Man sagt, er schnei­det die x-​Achse, wenn er an der Null­stel­le die x-​Achse von oben nach unten oder von unten nach oben durch­quert.

3
Zeich­ne in das Ko­or­di­na­ten­sys­tem Pa­ra­beln nach den Vor­ga­ben ein!
Nutze am Bes­ten un­ter­schied­li­che Far­ben.
  • eine Null­stel­le, Graph ver­läuft ober­halb der x-​Achse
  • eine Null­stel­le, Graph ver­läuft un­ter­halb der x-​Achse
  • zwei Null­stel­len, Graph nach oben ge­öff­net
  • zwei Null­stel­len, Graph nach unten ge­öff­net
  • zwei Null­stel­len, Graph nach unten ge­öff­net
  • keine Null­stel­le, Öff­nung egal
  • drei Null­stel­le, Öff­nung egal
−7−6−5−4−3−2−11234567x−5−4−3−2−11234567yoriginO−7−6−5−4−3−2−11234567x−5−4−3−2−11234567yoriginO
Bereitgestellt von: anonym Stand: 07.10.2025 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/nullstellen-quadratischer-funktionen-tx7whvrq
Seite: 2/3
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/nullstellen-quadratischer-funktionen-tx7whvrq
Input
Nullstellen quadratischer Funktionen
Mathematik Funktionen R 9

An­zahl der Null­stel­len einer qua­dra­ti­schen Funk­ti­on

Ab­hän­gig davon, wie der Graph der qua­dra­ti­schen Funk­ti­on aus­sieht, gibt es 3 Va­ri­an­ten:

Ab­hän­gig davon, wie der Graph der qua­dra­ti­schen Funk­ti­on aus­sieht, gibt es 3 Va­ri­an­ten:

1

2
3
4

Genau 1 Null­stel­le

Keine Null­stel­len

Genau 2 Null­stel­len

Null­stel­len ab­le­sen

Du kannst die Null­stel­len also aus den je­wei­li­gen Funk­ti­ons­gra­phen ab­le­sen.

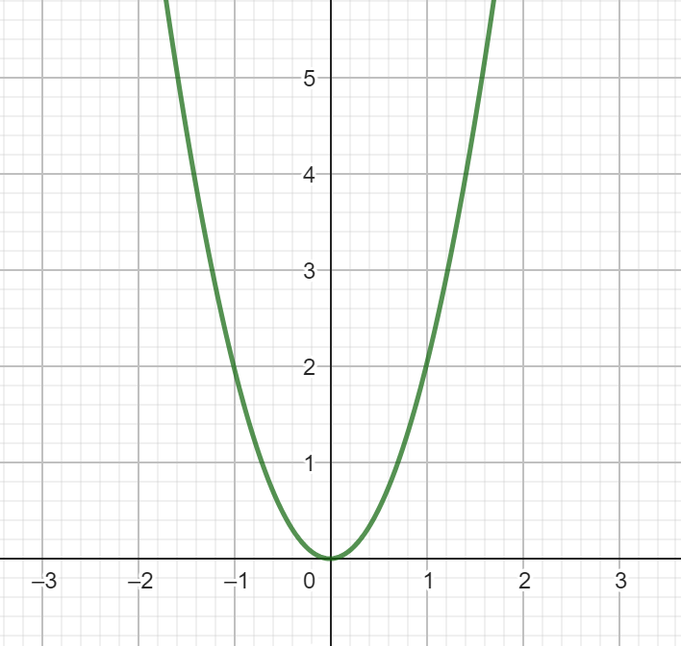
Die   hat genau eine Null­stel­le. Der Schei­tel­punkt liegt auf der x-​Achse. Statt Schnitt­punkt lässt sich in einem sol­chen Fall auch Be­rüh­rungs­punkt mit der x-​Achse sagen.

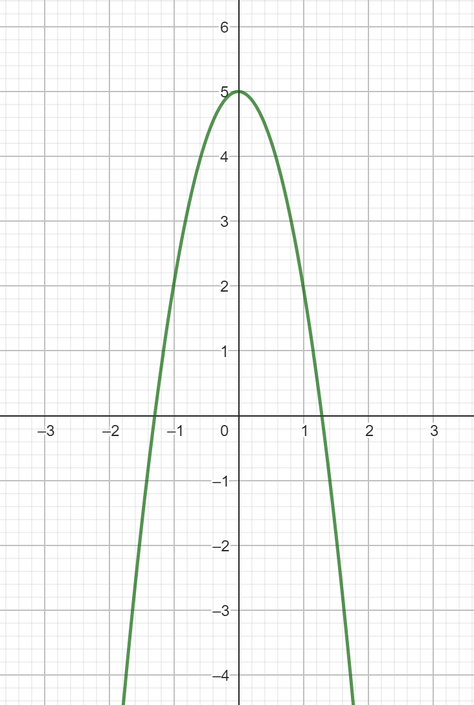
Die   hat ihren Schei­tel­punkt ober­halb der x-​Achse und ist nach unten ge­öff­net. Daher schnei­det sie die x-​Achse an zwei Stel­len. Es gibt also 2 Null­stel­len.

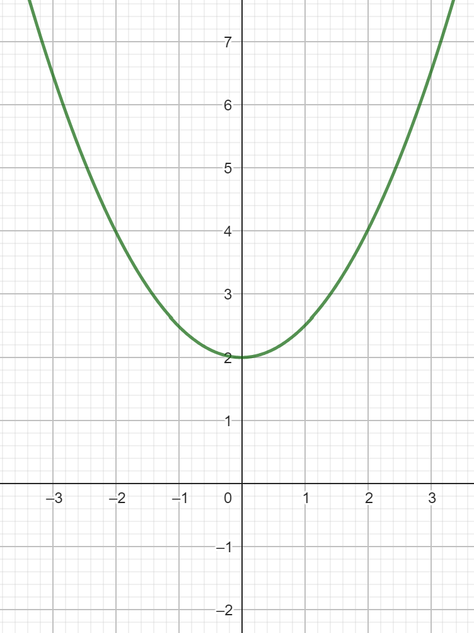
Die   hat gar keine Null­stel­len.

Rech­ne­ri­sches Be­stim­men von Null­stel­len

An­hand der Gra­fik der zwei­ten Funk­ti­on kön­nen wir zwar ab­le­sen, dass diese zwei Null­stel­len be­sitzt. Den ge­nau­en Wert kön­nen wir durch das Ab­le­sen hier al­ler­dings nicht genau be­stim­men. Daher be­nö­ti­gen wir eine Mög­lich­keit zur ge­nau­en Be­rech­nung von Null­stel­len. Das folgt in einem an­de­ren Ka­pi­tel.

Bereitgestellt von: anonym Stand: 07.10.2025 Lizenzhinweise: https://editor.mnweg.org/entdecken/dokument/nullstellen-quadratischer-funktionen-tx7whvrq
Seite: 3/3
Angaben zu den Urhebern und Lizenzbedingungen der einzelnen Bestandteile dieses Dokuments finden Sie unter
https://editor.mnweg.org/entdecken/dokument/nullstellen-quadratischer-funktionen-tx7whvrq
x