Der Rauminhalt wird oft auch Volumen genannt.
Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.
Oberflächen und Rauminhalte von Pyramiden
Gizeh - Die Großen Pyramiden von Ägypten kennst du sicher.
Pyramiden sind oft beeindruckende Bauwerke aus der Vergangenheit. Es gibt aber auch neue Bauwerke, die uns beeindrucken, wie z.B. der Louvre in Paris.
Louvre Museum in Paris
ToDo
Schau in deinem Tafelwerk nach den Formeln!
Volumen einer Pyramide
VPy = · AG · h
Oberflächeninhalt einer Pyramide
AO = AGrundfläche + 4 · ADreieck
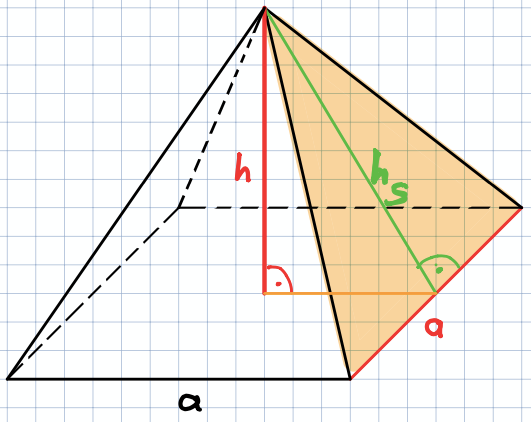
AO = AG+ 2 · a · hs (siehe Abb.)
(Anmerkung 4 · 0,5 = 2)
Oberflächenberechnung
Die Berechnung der Oberfläche ist eigentlich ganz logisch.
Der Mantel
der Pyramide besteht immer aus Dreiecken und die Grundfläche meist aus einem Quadrat.
Also: OPy = a · a + 4 · = a2 + 4 ·
Grundfläche: G = a · a = a2
Mantelfläche: M = 4 · Dreieck
= 4 · = 2 · a · hs
1
Beispiel: Volumen und Oberfläche einer Pyramide berechnen
Eine Pyramide hat die Seitenlänge a = 4 cm und die Höhe 5 cm.
Die Höhe der Dreiecksfläche hs beträgt 6 cm. Berechne das Volumen und den Oberflächeninhalt.
Eine Pyramide hat die Seitenlänge a = 4 cm und die Höhe 5 cm.
Die Höhe der Dreiecksfläche hs beträgt 6 cm. Berechne das Volumen und den Oberflächeninhalt.
