Hinweis zum Einsatz im Unterricht
at das gut funktioniert? Überprüfe die Lösungen, wenn du bisher nur die Hälfte wusstest, nutze die Anton-App:
Willkommen im Baustein Prozentrechnung
Nach diesem Baustein...
...kennst du den Zusammenhang
zwischen Bruch- und Prozentrechnung
...kannst du Beispiele für Prozente im
Alltag benennen und erklären.
...beherrschst du Aufgaben mit
einfachen Prozentangaben.
Benötigtes Material:
- Prozenttafel +Gummi
- Memory
- Prozentscheibe
- Arbeitsmaterial
(Achtung: ab hier brauchst du eine:n Arbeitspartner:in)
(1-2 Std.)
Vorwissen: Brüche
Brüche sind eine wichtige Voraussetzung für die Prozentrechnung. Deshalb ist es wichtig, dass du schon Brüche I und Brüche II bearbeitet hast.
Wir beginnen daher auch mit einer Wiederholung:
- Darstellung von Brüchen
- Berechnen von Anteilen
- Kürzen und Erweitern
Zur Wiederholung der Darstellung von Brüchen löse Aufgabe 1 und 2 auf dem Arbeitsmaterial. Auf dem Arbeitsmaterial kannst du schreiben und zeichnen.
Hat das gut funktioniert? Überprüfe die Lösungen. Wenn du bisher nur die Hälfte wusstest, nutze die Anton-App:
Lernpfad:
Mathematik 6. Klasse >> Brüche und gemischte Zahlen >> Brüche darstellen
Brüche nutzen wir, wenn wir z. B. von der Hälfte einer Pizza oder 3/5 einer Schokolade sprechen. Das nennt man auch den Anteil von einem Ganzen. Damit man dies jedoch nicht immer aufzeichnen muss (wie in Aufg. 1 und 2), gibt es ein Rechenschema.
Das erste Rechenschema findest du in Aufgabe 3 auf dem Arbeitsmaterial. Fülle die Lücken entsprechend. Um weitere Anteile zu berechnen, löse Aufgabe 4, 5 und 6.
Bevor wir jetzt tatsächlich mit den Prozenten beginnen, wollen wir nochmal das Kürzen und Erweitern trainieren:
Ein Bruch hat ganz viele unterschiedliche Zahlendarstellungen, man muss dazu nur Nenner und Zähler mit der gleichen Zahl multiplizieren oder dividieren.
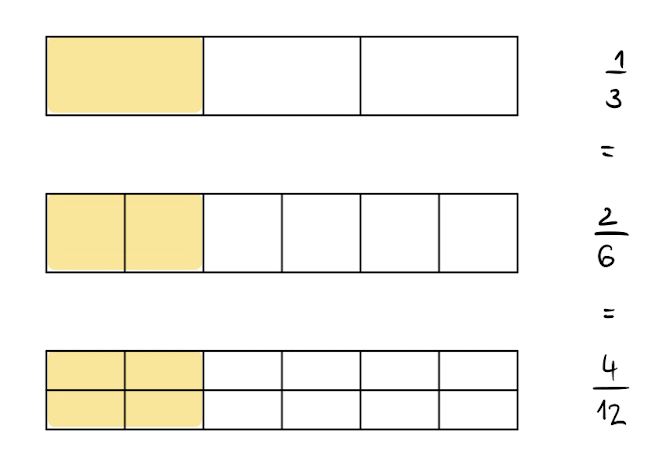
Dadurch unterteilt man das Ganze feiner (multiplizieren) oder gröber (dividieren).
Man rechnet:
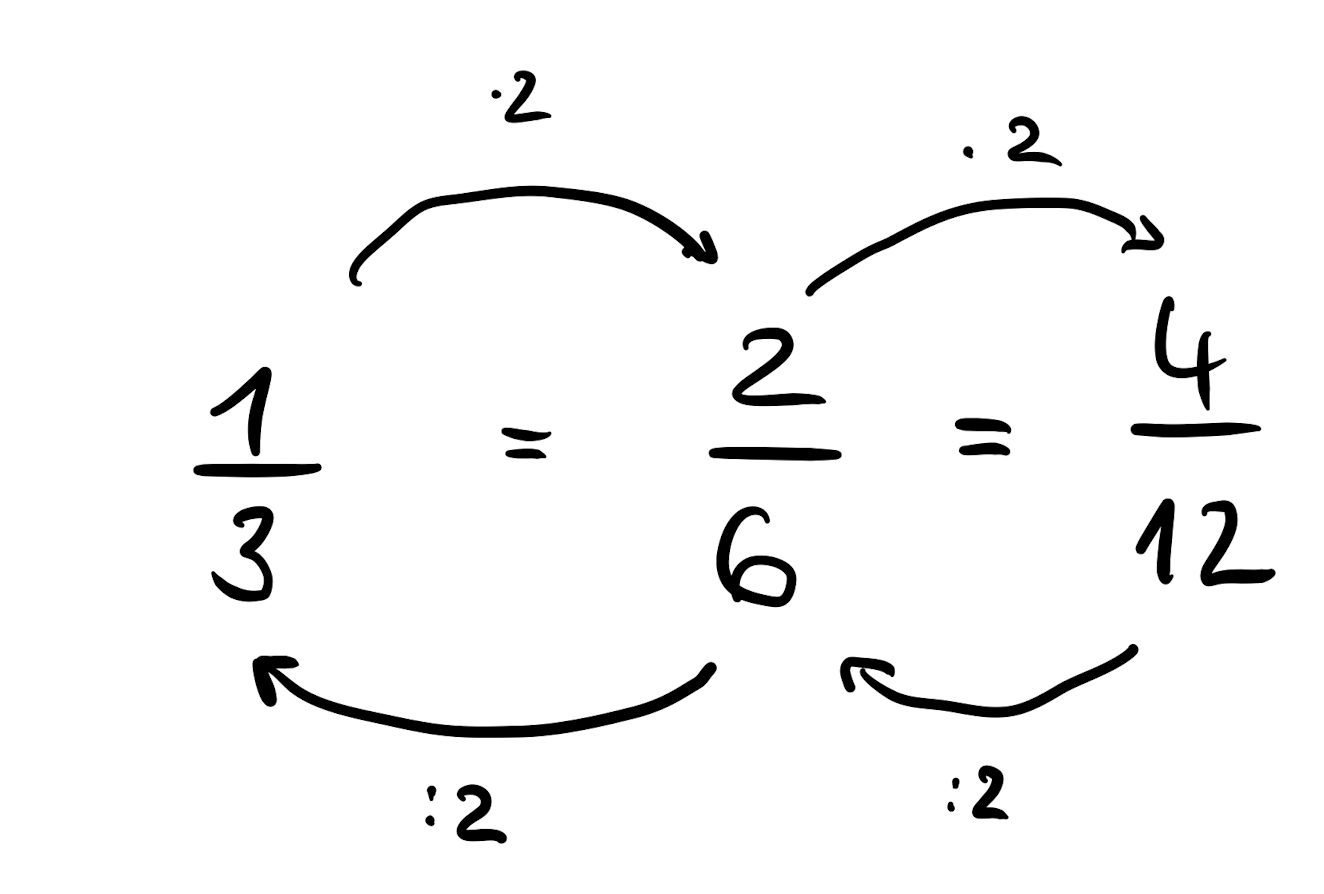
Löse nun Aufgabe 7.
Hat das gut funktioniert? Schaue danach in die Lösungen, falls du bisher nur drei richtige Ergebnisse hattest, nutze die Anton-App:
Lernpfad:
Mathematik 6. Klasse >> Brüche >> Brüche erweitern und kürzen
Prozente im Alltag
Prozente umgeben uns überall im Alltag und helfen uns bestimmte Angaben zu machen. Überlege, ob du mindestens zwei der Situationen kennst.
Fallen dir noch weitere Situationen ein, wo man so ähnliche Aussagen trifft?
Notiere mindestens zwei weitere Situationen in deinem Heft und
löse Aufgabe 8 auf dem Arbeitsmaterial.
Um jetzt tatsächlich mit Brüchen arbeiten zu können, schauen wir uns jetzt genauer an, was ein Prozent eigentlich bedeutet.
"Prozent" bedeutet genau genommen "Hundertstel". Das heißt, dass du auf Hundertertafeln verschiedene Prozente darstellen kannst, indem du die Kästchen farbig markierst oder mit dem Gummi abtrennst (siehe Material).
1 Kästchen ist
= 1% des Feldes
10 Kästchen sind
= 10% des Feldes
20 Kästchen sind
= 20% des Feldes
15 Kästchen sind
= 15% des Feldes
Nehmt euch eine Hundertertafel und bearbeitet die folgenden Aufgaben anhand des folgenden Beispiels.
Lisa spielt sehr gerne Fußball, wobei ihre Spezialität Elfmeterschüsse sind. Kannst du die folgenden Aufgaben für sie mit Hilfe einer Hundertertafel lösen? Notiere alle Lösungen in Prozent und als Hundertstelbruch.
- Im heutigen Training muss Lisa 100 Schüsse machen. Davon gehen 10 Schüsse ins Tor. Trenne den entsprechenden Abschnitt mit dem Gummi auf der Hundertertafel ab.
- Nun gibt es einen neuen Durchgang. Allerdings ist das Training bald zu Ende, sodass die Trainerin beschließt, nur noch 50 Schüsse durchzuführen. Lisa trifft wieder 10 mal.
Stelle auch dieses mal den prozentualen Anteil seiner Treffer mit den Hundertertafeln da. - Tausche dich mit deinem/deiner Partner:in über die folgende Frage :
Trifft Lisa besser in der ersten oder in der zweiten Runde?
aus und halte deine Lösung mit einer kurzen Begründung schriftlich fest.
Löse nun die Aufgaben 9 und 10 auf dem Arbeitsmaterial.
Übertrage zuerst die Tabelle in deinen Hefter.
Spielt dann zu zweit das Memory. Während des Spielens ergeben sich Zahlenpaare. Diese Paare tragt ihr in jeweils eine noch leere Zeile der Tabelle ein und ordnet die Karten einer Kategorie aus dem Kopf der Tabelle zu.
Im Anschluss füllt jeder für sich die leeren Kästchen aus. Ein Beispiel ist als Orientierung vorgegeben.
Bruch
Hunderstel
Prozent
50%
ACHTUNG PARTNER:INNENARBEIT
Nehmt euch eine Prozentscheibe aus dem Mathekoffer. Einer von euch stellt eine Prozentaufgabe (Prozentsatz) mit Hilfe der Markierungen auf der Rückseite der Prozentscheibe ein. Der/Die andere schätzt, welcher Prozentsatz eingestellt wurde.
ACHTUNG! Wenn du auf der gelben Rückseite z. B. 25% einstellst, dann muss auf der Vorderseite der blaue Anteil geschätzt werden!
- Suche dir drei Prozentsätze aus und stelle sie nacheinander auf der Scheibe ein: 25%; 75%; 90%, 30%; 5% 52%; 10%
- Überlegt euch selbst zwei weitere Prozentsätze und lasst euren Partner/ eure Partnerin schätzen!
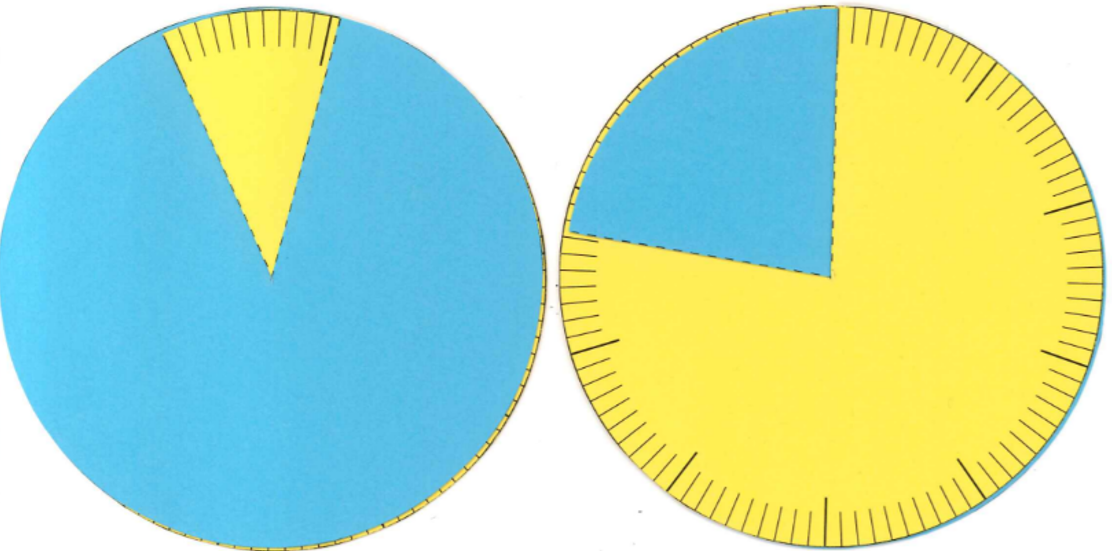
ACHTUNG PARTNER:INNENARBEIT
Nun schaut ihr euch nur die Vorderseite der Prozentscheibe an. Einigt euch auf einen Prozentangabe, die ihr gerne einstellen möchtet. Versucht gemeinsam die Prozentangabe so genau wie möglich zu erreichen. Dreht anschließend die Scheibe um und kontrolliert, wie nah ihr dran ward. Wiederholt diesen Vorgang noch zwei mal.
- Augustin, Ludwig (Hrsg.): Sekundo: Mathematik. 7, Förderh. Für differenzierende Schulformen, Dr. A., Braunschweig: Schroedel: 2013.
- Diez, Thomas (Hrsg.): Mathematik - Individuelles Fördern. 6: [Mit CD-ROM] / Autoren: Thomas Diez. Dr. A,1., 2010.
- O. V.: Klick. 6, Arbeitsheft: Arbeitsheft. 1. Aufl., 2013.
- Serlo: Prozente aus dem Alltag. URL: https://de.serlo.org/mathe/36759/prozente-aus-dem-alltag [Abruf am 01.12.2021].
