TitelQuadratzahlen - Wurzelziehen - Zehnerpotenzen
Autoranonym
veröffentlicht13.07.2025
FachMathematik
NiveaustufeM (Mindeststandard)
Phase9
MaterialformInformation

Um die Lizenzinformationen zu sehen, klicken Sie bitte den gewünschten Inhalt an.

Quadrieren

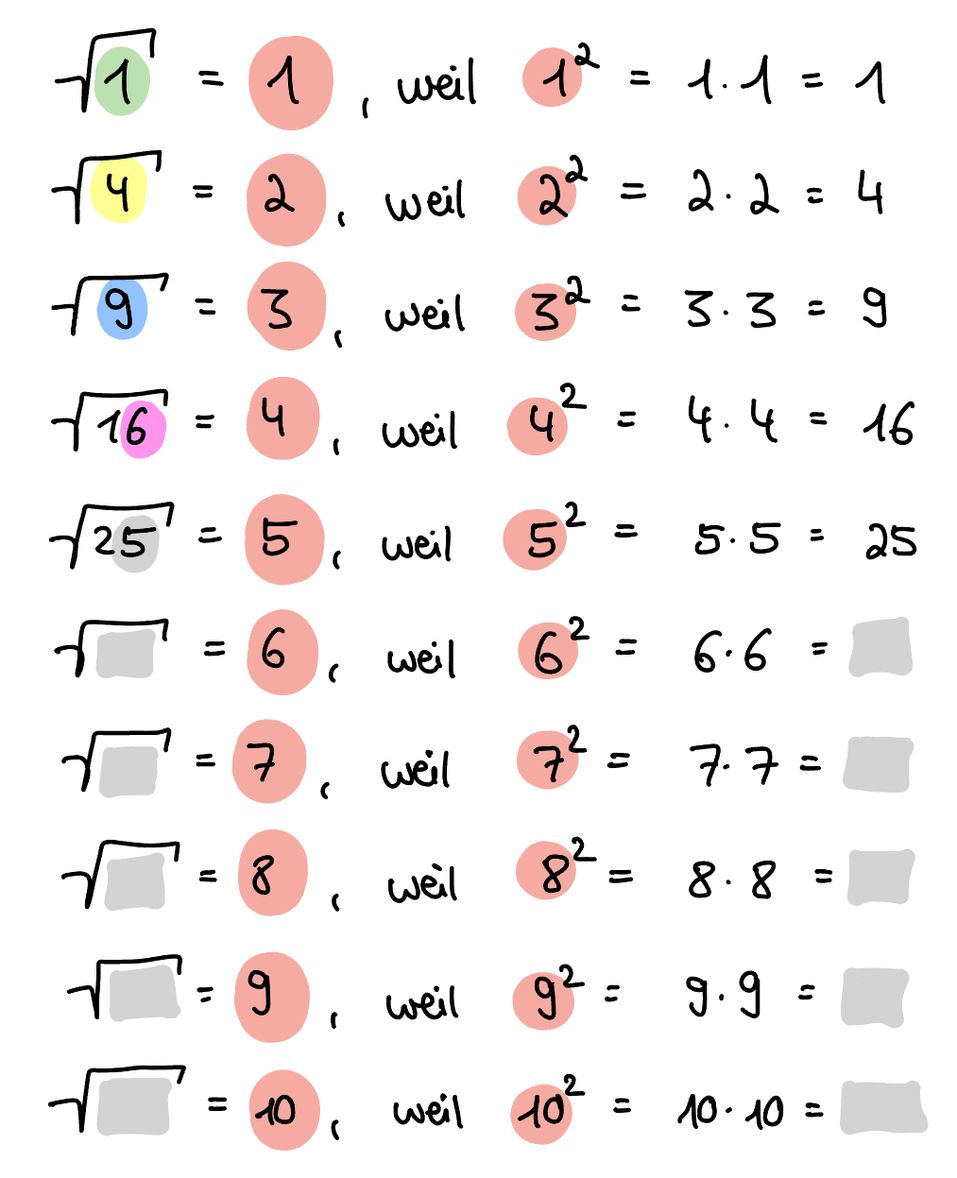
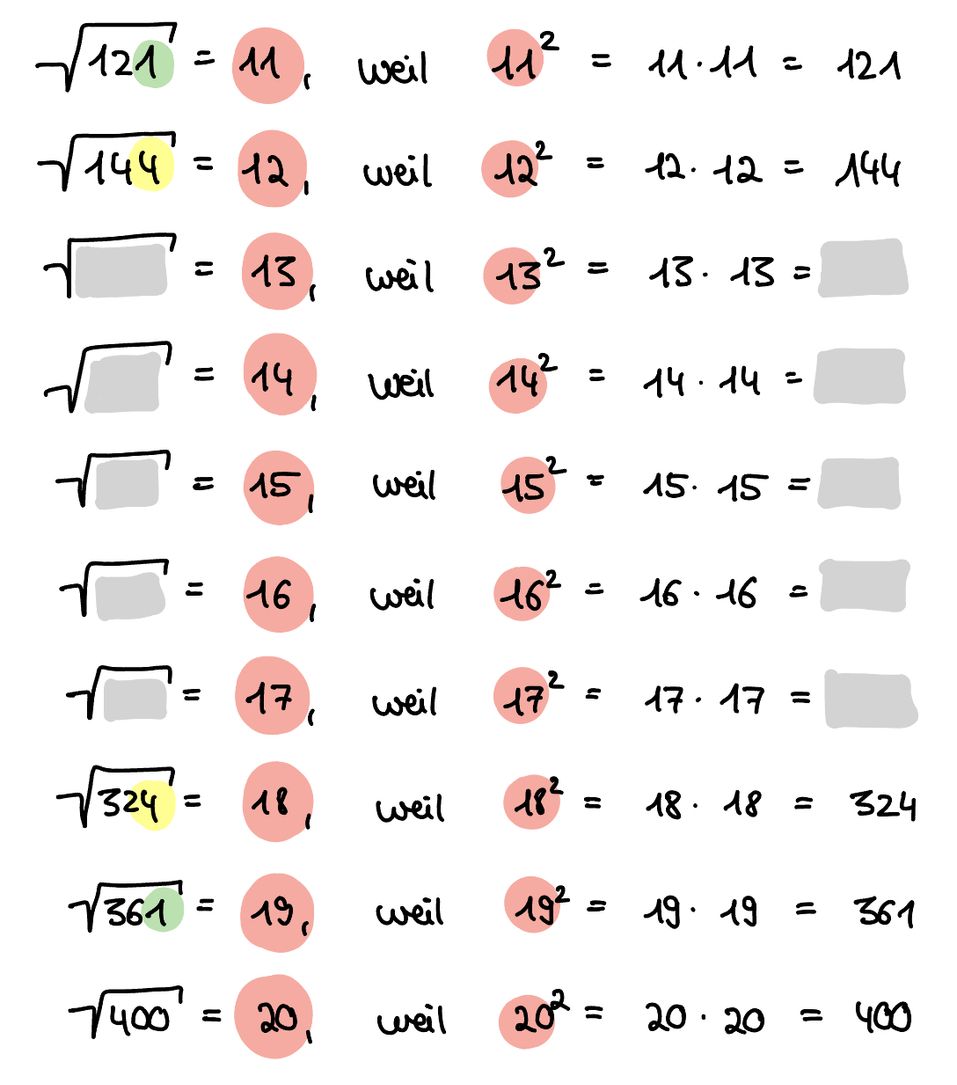
Quadratzahlen

... sind die Flächeninhalte von Quadraten mit einer Kantenlänge a mit natürlichen Zahlen.

a= 2

a= 3

a= 4

a= 5

a= 6

Zum Beispiel:

$4 \cdot 4 = 4^{2} = \underline{16}$

$5 \cdot 5 = 5^{2} = \underline{25}$

$8 \cdot 8 = 8^{2} = \underline{64}$

$11 \cdot 11 = 1 1^{2} = \underline{121}$

$13 \cdot 13 = 1 3^{2} = \underline{169}$

$17 \cdot 17 = 1 7^{2} = \underline{289}$

$1, 4 \cdot 1, 4 = 1, 4^{2} = \underline{1, 96}$

$1, 8 \cdot 1, 8 = 1, 8^{2} = \underline{3, 24}$

$2, 5 \cdot 2, 5 = 2, 5^{2} = \underline{6, 25}$

BEACHTE!

Achte auf die Vorzeichen:

ABER:

3^{2} = 3 \cdot 3 = 9

- 3^{2} = - (3 \cdot 3) = - 9

(- 3)^{2} = (- 3) \cdot (- 3) = 9

Die Quadratzahlen bis 20 solltest du auswendig wissen!

Lerne diese auswendig.

Quadratzahlen? - Die muss man auswendig lernen!

YouTube-Video

$0^{2} = 0$
$1^{2} = 1$
$2^{2} = 4$
$3^{2} = 8$
$4^{2} = 16$
$5^{2} = 25$
$6^{2} = 36$
$7^{2} = 49$

$8^{2} = 64$
$9^{2} = 81$
$1 0^{2} = 100$
$1 1^{2} = 121$
$1 2^{2} = 144$
$1 3^{2} = 169$
$1 4^{2} = 196$
$1 5^{2} = 225$

$1 6^{2} = 256$
$1 7^{2} = 289$
$1 8^{2} = 324$
$1 9^{2} = 361$
$2 0^{2} = 400$
$2 5^{2} = 625$

Wurzelziehen

Einstiegsfrage

Der Landschaftsgärtner soll einen Swimming-Pool

für Familie Betz im Garten bauen.

Dieser soll quadratisch und 16 m² groß sein.

Wie lang und breit muss das Loch sein,

welches der Landschaftsgärtner gräbt?

Lösungsweg

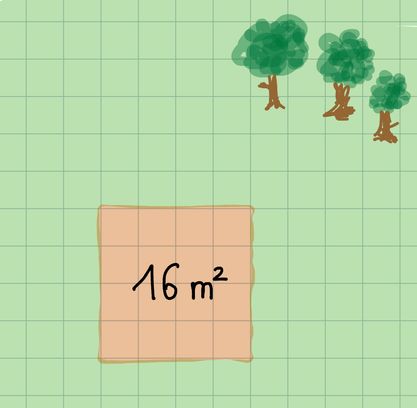
Am einfachsten erhältst du die Lösung durch das

Wurzelziehen:

Antwort: Der Pool ist 4m breit und lang.

16 = 4

4^{2} = 4 \cdot 4 = 16

weil

Merke:

Die Quadratwurzel einer Zahl a ist jene positive Zahl,

deren Quadrat gleich der gegebenen Zahl a ist.

Unter der Wurzel darf NIE ein Minus stehen!

b^{2} = b \cdot b = a

a = b

weil

Beispiel:

3^{2} = 3 \cdot 3 = 9

9 = 3

weil

Wurzelziehen ist also die Umkehrung von Quadrieren.

Quadratwurzel ziehen | Lehrerschmidt

YouTube-Video

Der Radikand

Als Radikand wird die Zahl bezeichnet, die unter der Wurzel geschrieben ist. Der Radikand darf in den uns bisher genutzten Zahlenräumen nicht negativ sein!

Quadratwurzel ziehen | Wurzel ziehen

YouTube-Video

Wichtige Quadratwurzeln selbst entdecken:

Bestimme die fehlenden Zahlen.
Was fällt dir auf?
Schaue dir auch die letzten Ziffern der Quadratzahlen
und der Zahlen unter der Wurzel an!
Lerne diese auswendig!

Merke

Negative Zahlen können quadriert werden, aus negativen Zahlen kann jedoch keine Wurzel

gezogen werden (siehe nächste Beispiele).

Beispiele zum Quadrieren und Wurzelziehen:
Tipp: Lösungen immer abdecken!

11 · 11 =
11² = 121
0,3 · 0,3 =
0,3² = 0,09
(-5) · (-5) =
(-5)² = 25 $\to$ das Ergebnis wird positiv, da - · - = +
$100$ =
$10 \cdot 10$ = 10
$- 100$
$\to$ keine Lösung
Schau mal, was dein Taschenrechner anzeigt.
$(\frac{2}{3})^{3}$ =
$(\frac{2}{3}) \cdot (\frac{2}{3}) \cdot (\frac{2}{3}) = \frac{8}{27}$

Die Zehnerpotenzen funktionieren im Prinzip genauso wie das Quadrieren,
nur, dass es neben der Hochzahl ² noch größere oder negative Hochzahlen gibt.

10² = 10 · 10 = 100
10³ = 10 · 10 · 10 = 1.000
10⁴ = 10 · 10 · 10 · 10 = 10.000
Was ist also 10¹? Richtig: 10¹ = 10
Zehnerpotenzen können auch addiert, subtrahiert
und multipliziert werden.
Wie das geht, siehst du in den Beispielen.
Merke: 10⁰ = 1 (hoch ⁰ ist immer 1 also auch 7⁰ = 1)
Was ist dann 10 ^-1 ?
Denke einmal drüber nach. Das kommt dann in einer der nächsten Einheiten.

Allgemeine Wurzeln ziehen ohne Taschenrechner, mit der Intervallschachtelung.

Um eine Wurzel zu ziehen, musst du immer dir bekannte Quadratzahlen mit dem Radikand vergleichen. Du wählst ein Intervall, also einen Zahlenbereich, in dem die Wurzel liegt und verkleinerst den Intervall immer wieder ein bisschen, bis du die gewünschte Zahl erreicht hast.

Gesucht ist das Ergebnis von

110, 25 =

$100 = 10$
Das Ergebnis ist größer als $10$ .
Die Mitte von $10$ und $11$ ist $10, 5$ also wird $10, 5^{2}$ berechnet.
$110, 25 = \underline{10, 5}$

$121 = 11$
Das Ergebnis ist kleiner als $11$ .
$10, 5^{2} = 110, 25$
Radikand erreicht und Rechnung beendet.

Falls man damit noch nicht zum richtigen Ergebnis kommt, probiert man es nach diesem Prinzip weiter.

Qua­drie­ren

Wur­zel­zie­hen

Quadrieren

Wurzelziehen